自动搬运

查看原文

来自洛谷，原作者为

	Mydeimos 念念不忘，必有回响||支持路关

搬运于2025-08-24 22:52:15，当前版本为作者最后更新于2025-01-16 21:25:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

1. 思维 + 树形 dp 题。

2. 题意：

左边为单调不下降，右边为单调不上升的部分为山顶，可以任意移走土块，但显然是一个一个山顶去移走，求最多留下 $k$ 个山顶时的最小移走土数。

3. 思路：

提供一种加强版 $n$ 为 $10^5$ 也能过的方法。

时间复杂度为 $O( n \times k^2 )$。

做法不难，但细节较多。 先将山分为多块，也是矩阵，划分方法如下图。

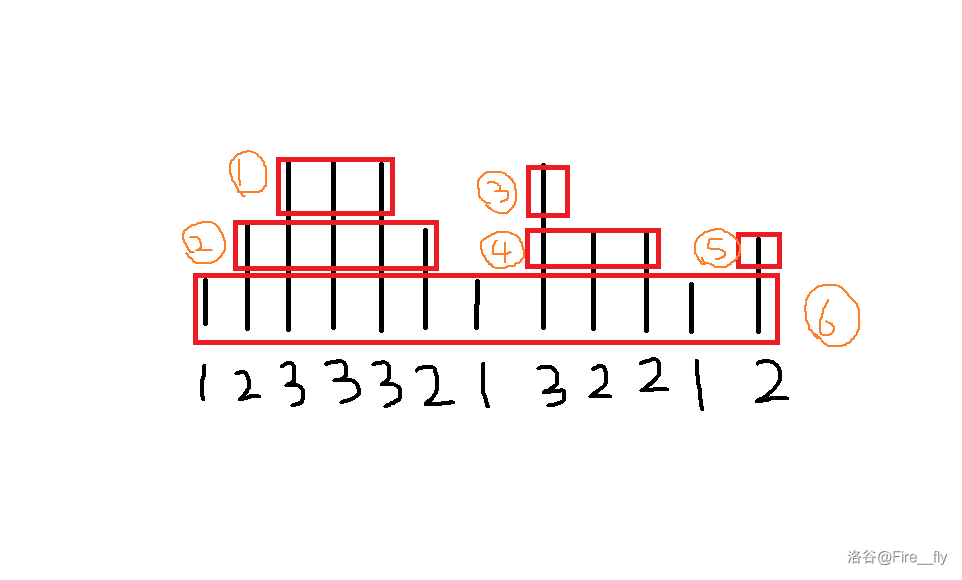
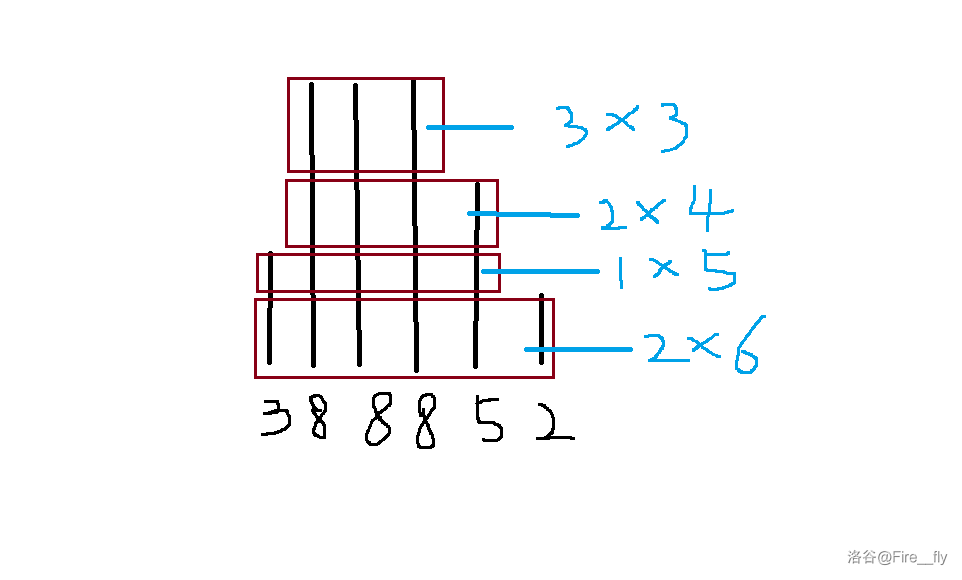
即将一个山顶划分为不同层的矩阵，

然后对矩阵建立从属关系，及左右边界是否包含。

下图黑字为编号，蓝字为块大小。

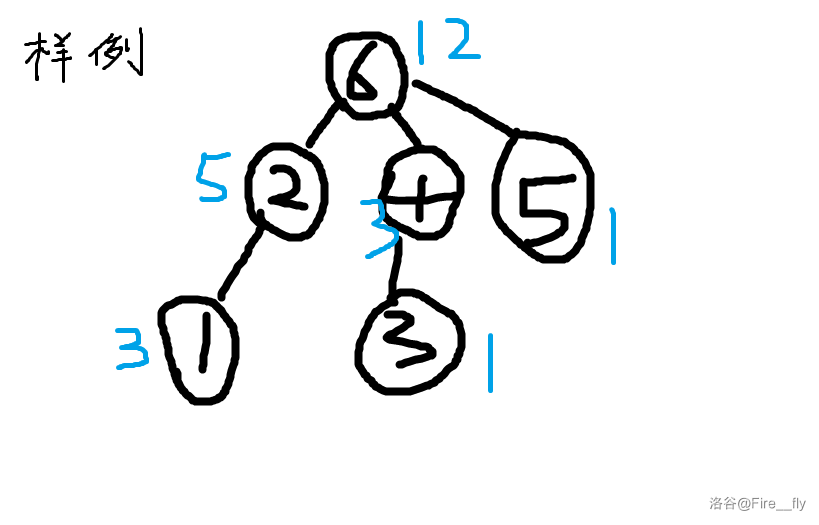
再利用块大小做一个树形 dp，具体转移如下，有具体解释。

4. 代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define N 100005
#define M 26
#define inf 1000000000000007
ll n,m,u,v,ans=inf,f[N][M],p; 
ll a[N],b[N],cnt;
ll q[N],qq[N],cnt1=1;
ll t[N],cnt2;
//f[i][j]为编号为i的块及其子树内 有j个山顶的 最小移走土数 
//a为该块大小  b为该块最左点下标  cnt为对应的块数
//q，qq为队列  cnt1为对应队内数  q为高度，是单调序列  qq为对应的最左点 
//t为可能为从属块队列，单调递增，且无包含关系  cnt2为对应队内数  
vector<ll>s[N];//记录块从属关系 
void dfs(ll x,ll y) {//树形dp 
	if(!s[x].size()) f[x][1]=0;//若x为叶子结点，则其自身为山顶 
	for(auto i:s[x]) if(i!=y) {
			dfs(i,x);
			a[x]+=a[i];//算x子树大小 
			for(ll j=m; j>=0; j--) {//按从大到小，先更新留下山顶多的 
				for(ll k=m-j; k>=1; k--) f[x][j+k]=min(f[x][j+k],f[x][j]+f[i][k]);//i的山顶移走k个，x内共j+k个山顶 
				f[x][j]+=f[i][0];//i的山顶全部移走 
			}
		}
	f[x][0]=a[x];//x全移走 
	return;
}
int main() {
	scanf("%lld%lld%lld",&n,&m,&u);
	q[cnt1]=u;
	qq[cnt1]=1;
	for(ll i=2; i<=n; i++) {
		scanf("%lld",&u),p=i;
		while(1) {
			if(q[cnt1]<=u) break;//山顶左侧必为单调不下降增
			p=qq[cnt1];
			v=q[cnt1]-u;
			if(cnt1>1) v=min(v,q[cnt1]-q[cnt1-1]);
			++cnt;
			a[cnt]=v*(i-qq[cnt1]);//计算块大小 
			b[cnt]=qq[cnt1];//块的最左点 
			while(cnt2&&b[cnt]<=b[t[cnt2]]) s[cnt].push_back(t[cnt2]),cnt2--;// 连接从属块，记得删掉被连了的 
			++cnt2;
			t[cnt2]=cnt;
			cnt1--;
		}
		if(q[cnt1]<u) ++cnt1,q[cnt1]=u,qq[cnt1]=p;//同高度不必多加入队列，因为前面的更左 
	}
	u=q[cnt1];
	while(cnt1) {//同上可得 
		++cnt;
		a[cnt]=(n+1-qq[cnt1])*(u-q[cnt1-1]);
		b[cnt]=qq[cnt1];
		u=q[cnt1-1];//更新高度 
		while(cnt2&&b[cnt]<=b[t[cnt2]]) s[cnt].push_back(t[cnt2]),cnt2--;
		++cnt2;
		t[cnt2]=cnt;
		cnt1--;
	}
	for(ll i=1; i<=cnt; i++) for(ll j=1; j<=m; j++) f[i][j]=inf;//初始化，j必须从1开始 
	dfs(cnt,0);
	for(ll i=1; i<=m; i++) ans=min(ans,f[cnt][i]);//不一定有m个山顶 
	printf("%lld",ans);
	return 0;
}