自动搬运

查看原文

来自洛谷，原作者为

	EdenSky 壶关见主页 || NOIP RP ++ || 主页 https://www.luogu.com/article/w68nh64h

搬运于2025-08-24 22:52:13，当前版本为作者最后更新于2024-08-05 09:41:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P9830 Traveling in the Grid World

• 或许更好的阅读体验

思路分析

分析样例：

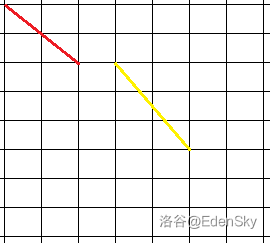
见红线，长宽各为 2，存在格点；黄线长 2 宽 3，没有格点。

考虑延长黄线使得长 4 宽 6，发现有格点。思考格点，如果长和宽都可以被分成 $p\times l$ 的格式，则存在格点。那么，就能想出：

推论 1：对于 $(0 \ , \ 0)$ 和 $(x \ , \ y)$ 之间没有格点，当且仅当 $\gcd(x \ , \ y )=1$。

对推论 1 的证明：

若存在格点 $A$，其坐标为 $(a \ , \ b)$，由于在同一直线上，斜率 $k$ 相同，则有 $k=\dfrac{a}{b}=\dfrac{x}{y}$，即 $b=\dfrac{a\times y}{x}$。由于 $b$ 为整数，则有 $x \ | \ a\times y$。

采用反证法，$\gcd(x \ , \ y )=1$ 时存在格点。

由于互质，$x=\prod\limits_{i=1}^{s1}p_i^{c_i} \ , \ y=\prod\limits_{i=1}^{s2}q_i^{d_i}$，假设 $x \ | \ y$，$y$ 必然有因子 $\prod\limits_{i=1}^{s1}p_i^{c_i}$，而实际上没有，所以 $y$ 对该式没有贡献。即：$x \ | \ a\times y \Longleftrightarrow x \ | \ a$。

而 $A$ 是线段上一点，有 $a<x$，又由于有 $x \ | \ a \Longrightarrow x \leq a$，冲突，由此可证。

得出推论 1 后，我们就能判断两点之间是否有格点了。那么如何得出最短答案呢？

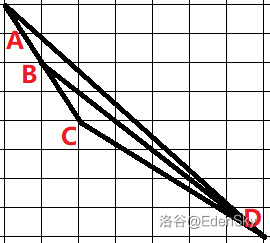
（图是随手画的，具体有的性质以下文所述为准。）

见上，假设 $AD$ 之间存在格点（在之后称为不合法），于是我们找到任意一点 $C$ 进行更新。

假设 $C$ 为不合法，以图为例，在 $AC$ 上可以取一格点 $B$，根据三角形定则 $| \ BD \ |>| \ BC \ |+| \ CD \ |$，则 $B$ 更优。假设无法在 $AB$ 和 $BD$ 上取格点，那么 $B$ 的取点是合法的，可以得出：

推论 2：对于任意不合法的取点，必然可以在原线段取到更优的合法方案。

那么就有：

推论 2.1：最优方案必然是合法的。

对推论 2.1 的证明：

假设最优方案不合法，根据推论 2，则有更优方案可以更新，与原有条件冲突，由此可得。

以上是一个转折点的情况，那如果有多个转折点呢？

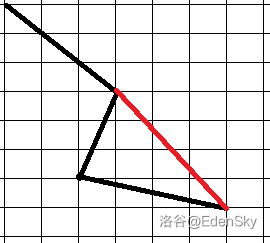
如图，多个转折点的情况是不需要考虑的，见图，由于三角形定则，红色线的长度小于另外两条边之和。换句话说：

推论 3：最优方案只转折一次或零次。

于是我们只要枚举一个点就可以了，如果在整个 $n\times m$ 的范围枚举，寻找最优方案，但这个时间复杂度显然是不合理的。其实我们只需要枚举线段附近的点就可以，这样复杂度就可以变成 $\mathcal{O}(n)$。

代码实现

#define by_wanguan
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
int t,n,m,y11,y2,y3,g; double dn,dm,nowm,ans,k;
double dis(double a,double b,double x,double y){
  return sqrt((x-a)*(x-a)+(y-b)*(y-b));
}
void solve(){
  k=(double)m/n;//斜率
  if((g=__gcd(n,m))==1)
    {printf("%.15lf\n",dis(0,0,n,m)); return ;}
  dn=n,dm=m;
  for(int i=1;i<n;i++){
    nowm=k*i;
    y11=(int)(nowm),y2=y11+1,y3=y11-1;//x坐标为i时附近的点的y坐标
    if(__gcd(n-i,m-y11)==1&&__gcd(i,y11)==1&&abs(y11-k*i)>1e-10)
    //判断是否合法，abs()是在判断是否为原线段上的点
	  ans=min(ans,dis(i,y11,n,m)+dis(0,0,i,y11));
    if(__gcd(n-i,m-y2)==1&&__gcd(i,y2)==1&&abs(y2-k*i)>1e-10)
      ans=min(ans,dis(i,y2,n,m)+dis(0,0,i,y2));
    if(__gcd(n-i,m-y3)==1&&__gcd(i,y3)==1&&abs(y3-k*i)>1e-10)
      ans=min(ans,dis(i,y3,n,m)+dis(0,0,i,y3));
  }
  printf("%.15lf\n",ans);
}
int main(){
  scanf("%d",&t); while(t--){
  scanf("%d%d",&n,&m);
  ans=1e9;
  solve();
}
} 

喵。