自动搬运

查看原文

来自洛谷，原作者为

	SpadeA261 **

搬运于2025-08-24 22:51:31，当前版本为作者最后更新于2023-10-30 01:42:54，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

写一种考场上想到的线性做法。

根据性质，若 $s[i,j-1]$ 与 $s[j,k]$ 均为合法子串，那么 $s[i,k]$ 必为合法子串。

考虑 dp，设 $f_i$ 表示以第 $i$ 位作为结尾的合法子串数量，容易得出转移方程：$f_i=f_{g_i-1}+1$，其中 $g_i$ 表示最大且能使 $s[g_i,i]$ 成为合法子串的下标。答案即为 $\sum_{i=1}^n f_i$。

由于 $g_i$ 是满足条件中最大的，因此必有 $s_i=s_{g_i}$，我们就可以按下图的方式从 $i$ 往前跳，初始时 $g_i=i-1$，之后不断令 $g_i\rightarrow g_{g_i}-1$，直到满足 $s_i=s_{g_i}$。

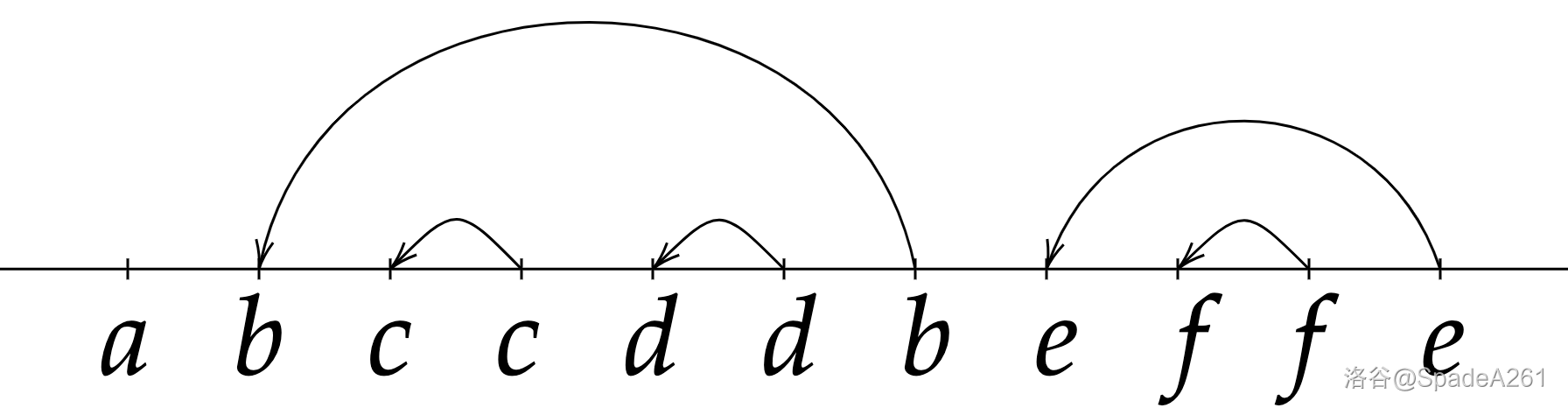
该做法的时间复杂度为 $O(|\Sigma|n)$，足以通过本题。考虑如何更进一步优化。

如果令 $h_i=g_i-1$，会发现跳的方式变成了这样，形成了若干条链，由此在每个位置记录 $a_{i,c}$，表示 $s_{a_{i,c}+1}=c$ 且能使 $[a_{i,c}+1,i]$ 成为合法子串的最大的下标。

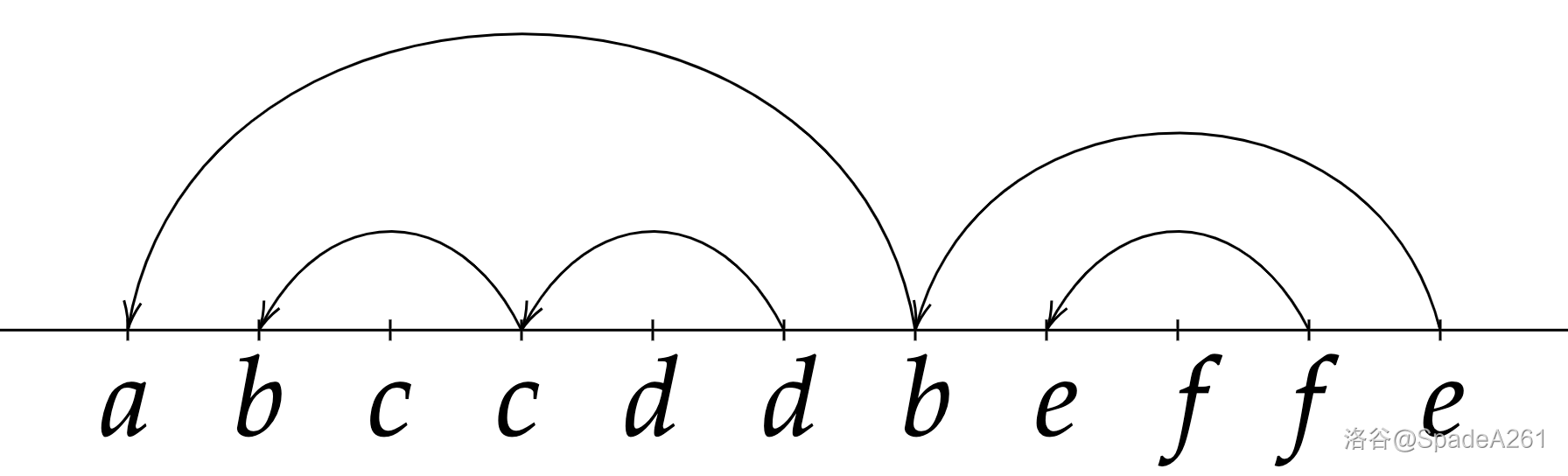
每次修改的值只有 $a_{i,s_i}$，我们便可以用 $to_i$ 表示该链的链头，每次修改 $a_{to_i,s_i}$ 即可。

时间复杂度：$O(n)$。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e6+5;
int n,dp[N],a[N][26],to[N];
char s[N];
ll ans;
int main()
{
    scanf("%d%s",&n,s+1);
    for(int i=1;i<=n;i++)
    {
        to[i]=i;
        int x=a[to[i-1]][s[i]-'a'];
        if(x) to[i]=to[x-1],dp[i]=dp[x-1]+1;
        a[to[i]][s[i]-'a']=i,ans+=dp[i];
    }
    printf("%lld\n",ans);
    return 0;
}