自动搬运

查看原文

来自洛谷，原作者为

	WhitD %$@oma

搬运于2025-08-24 22:50:13，当前版本为作者最后更新于2023-09-12 11:18:55，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目大意

给定一个具有 $n$ 个顶点和 $m$ 条边的无向图，找到一个图的生成树，使得生成树中的每个顶点的度数不大于 $\frac{n}{2}$。

思路

对于有 $n$ 个点的生成树，其边数为 $n-1$，总度数为 $2n-2$，因此至多只有一个点的度数会大于 $\frac{n}{2}$。

我们可以先把这个图的任意一个生成树找出来，然后找到这个生成树中度数大于 $\frac{n}{2}$ 的点（要是找不到说明这个生成树已经满足条件了，直接输出就可以），将这个点设为生成树的根节点，枚举所有不在生成树上的边，先将这条边加进去，然后判断图中是否形成了包含根节点的环……

如图：蓝色边是初始生成树，红色点是根节点，黄色边是当前枚举到的边，不难看出图中的绿色边形成了一个包含根节点的环。

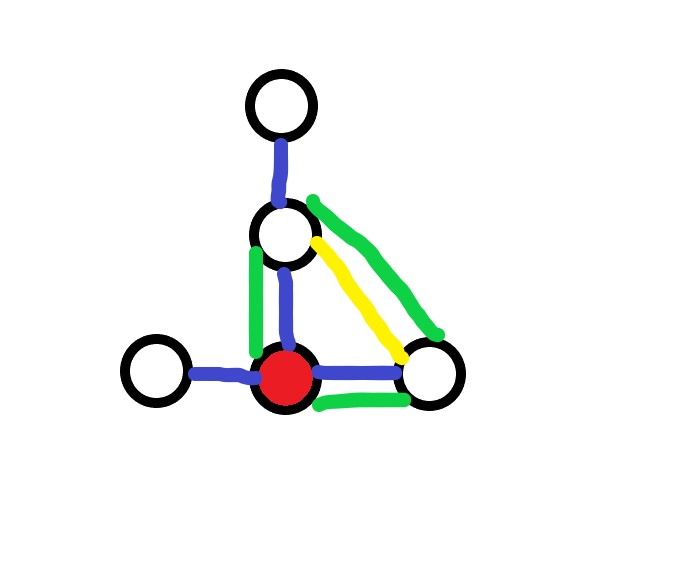
此时我们需要删除一条绿色边才能保证还是生成树，请注意我们的目的是为了减小根节点的度数，因此一定是优先删除与根节点相连的边，会有如下两种情况：

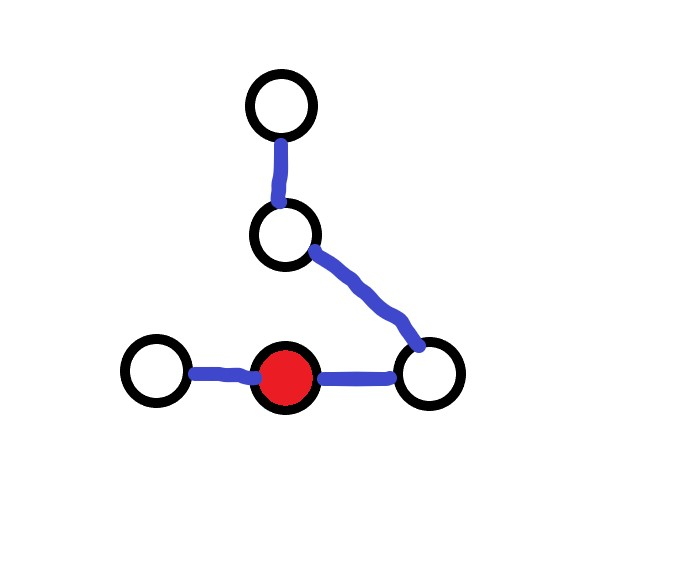
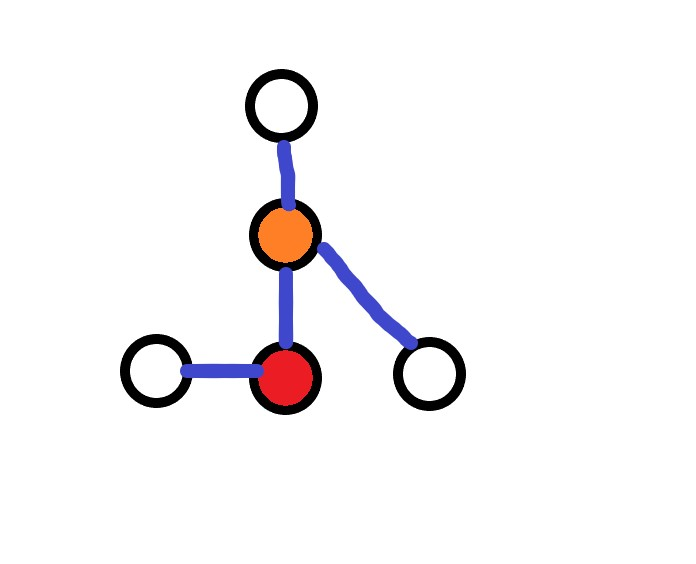
注意第二种情况，虽然根节点的度数小于 $\frac{n}{2}$ 了，但是橘色点的度数又大于 $\frac{n}{2}$ 了。我们发现原生成树中橘色点的度数为 $2$，而右下角的点度数为 $1$，也就是说我们在删边时需要优先删除度数大的点与根节点所连的边。

综上，我们得到了在删边时需要遵守的规则：优先删除与根节点相连的边，并且是度数大的节点与根节点相连的那条边（注意特判无解情况）。