1 条题解
-
0
自动搬运
来自洛谷,原作者为

璀璨星空1
倘若我们义无反顾去做不可能之事,世上便再没有不可能。搬运于
2025-08-24 22:50:02,当前版本为作者最后更新于2023-09-09 06:13:52,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
如溪水潺潺淌过古街 带走了如梦般的时节
小桥上人潮络绎不绝 牵引我思绪层出不迭我们的程序将分两个阶段进行。在第一阶段中,我们从 出发走到 ,找到并标明一条从 到 的最短路;在第二阶段中,我们从 出发走回 ,在回溯的过程中将所有不在最短路上的格子的标记清零。
第一阶段:标明一条从 到 的最短路。
我们先思考 ,即一棵树的情形。我们从 开始 DFS。设当前 DFS 到 ,我们需要枚举 个方向,并依次扩展那些 并且不同于来时的路的方向。我们有两种选择:
- 用一个 的颜色 记录当前扩展到了哪个方向,每次访问到 就将 增加 ;
- 每当 DFS 完一个 没找到通向 的路,就将 改成 ,表示将 这个格子堵住。
可以看出,采用第一种选择将大大增加所用的颜色个数。所以我们倾向于采用第二种选择。在 中我们继续沿用第二种选择:当 DFS 完 的某个儿子 时,就将 改成某种特殊的标记,表示以 为根的 DFS 已经结束。
再思考 。 保证了最短路 ,也就是说我们只会向右走或向下走。相比于 , 的简单之处在于我们只需要找到某一条从 到 的路径,这条路径便自然是最短路。
如果采用第二种选择的话,我们沿用 的 DFS 就可以直接解决 。可以获得 分。
有了 的提示,我们再来思考 。要求从 到 的路径最短,我们非常希望 BFS 而不是 DFS。但是由于 Pulibot 的视角是局部的,它天然更适合 DFS 而不是 BFS。
所以我们采用类似迭代加深的办法。我们一轮一轮扩展,在第 轮标记所有 的 。我们会遇到一个重要的问题:
- 在第 轮开始的时候,与 的 接触的 一定是 的。但是给 做了标记以后, 这个格子就与外界接触了。怎么防止 的 继续扩展下去,导致 的格子在第 轮就被标记呢?
考虑 BFS 树。我们每次扩展一层叶子。我们用 个方向 记录一个 在 BFS 树上的父亲,在遍历 BFS 树的时候,我们只能沿着父亲到儿子的方向走。这样我们便不可能沿不同的路径多次访问到同一个 。再加上 这 种颜色,总共是 种标记:
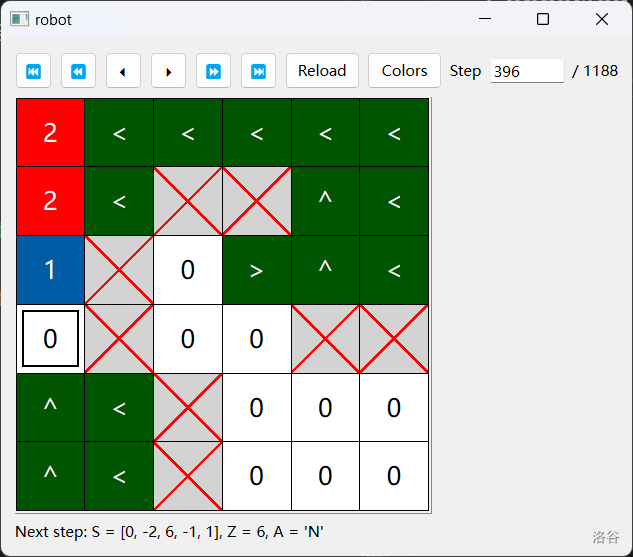
若不识梁祝变成蝴蝶 驾紫烟穿过天上宫阙
绝不知人间多愁离别 吹落叶散作秋风清切现在我们设计 DFS 的具体流程。在第 轮,我们沿着 BFS 树的第 到 层进行 DFS,扩展出它的第 层。设当前 DFS 到了 ,那么从 到 路径上的所有格子都 。 的 个邻居中一定有一个 ,那是 的父亲 。
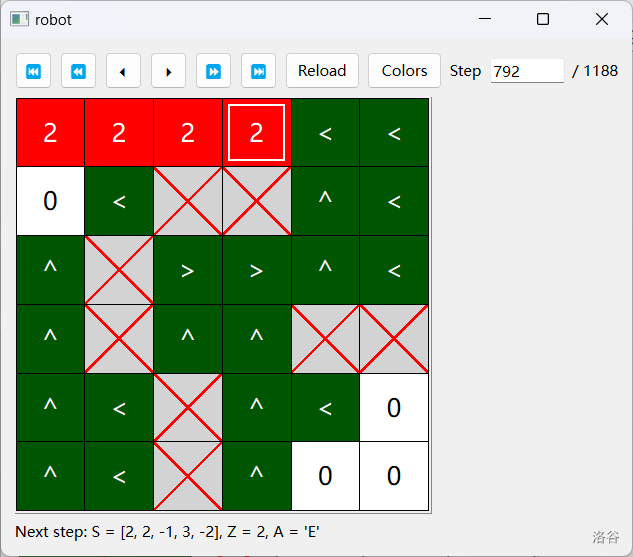
如果 的其他 个邻居中有指向 的箭头,则说明 不是叶子。我们按西、南、东、北的顺序找到第一个指向 的 ,走到 ,然后将 改成 ,从 出发继续 DFS。
如果 的其他 个邻居中没有指向 的箭头,则说明 是叶子。我们需要将 所有 的邻居 指向 ,然后立刻回溯。我们先将 改成 。当 Pulibot 站在一个 上时,它会按西、南、东、北的顺序找到第一个 的 ,走到 ,然后将 指向 并走回 ;如果 个邻居中已经没有 了,说明 的子树已经扩展完了,我们将 改成 ,并返回 ,标示从 到 这条路已经扩展完了。
当 的子树扩展完了的时候,我们选择将 改成 作为特殊的标记。这样做是很方便的:当 的儿子都扩展完了之后, 的周围一圈都是 ,然后 就会变成 并且将周围的 都重新指回 ,最后 再从 变成 。
最后当 并且 的 个邻居都 的时候,就意味着第 轮已经结束了。我们将 改成 ,从此开启第 轮。
整理前述的所有东西,我们得到了一个初步的做法:
- 如果 :
- 如果 ,则将 改成 并停在原地;
- 否则检查 的 个邻居。若邻居中有 ,则按西、南、东、北的顺序找到第一个 ,将 指向那个 并走过去。
- 如果 :
- 检查 的 个邻居。若邻居中有 ,则按西、南、东、北的顺序找到第一个 ,直接走过去;
- 否则如果 ,则将 改成 并停在原地;
- 否则检查 的 个邻居。若邻居中有 ,则按西、南、东、北的顺序找到第一个 ,将 改成 并走过去。
- 如果 :
- 检查 的 个邻居。若邻居中有指向 的 ,则按西、南、东、北的顺序找到第一个 ,直接走过去;
- 否则将 改成 并停在原地。
- 如果 ,则将 改成 并停在原地。
最后,我们将会到达下图所示的局面。直接沿着标明的最短路返回并将路径上的 都改成 ,可以获得 分。
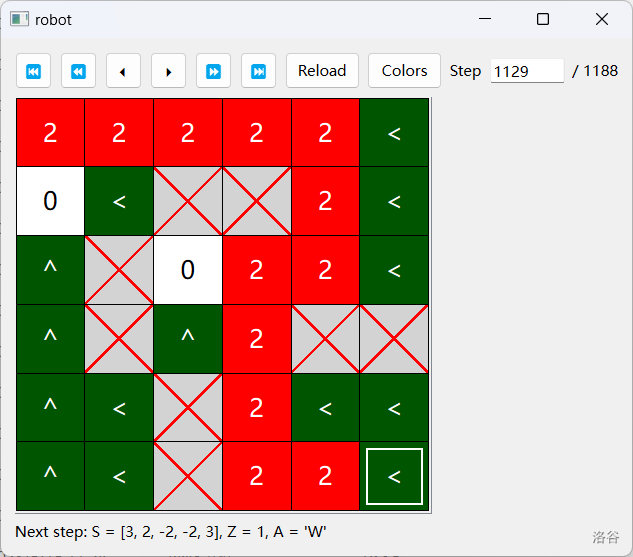
第二阶段:回溯清理所有不在最短路上的格子的标记。
最后我们再考虑回溯清理的问题。当 Pulibot 走到了 并且 时,意味着已经找到并标明了一条从 到 的最短路,应该开始回溯清理了。我们的目标是到达下图所示的局面:
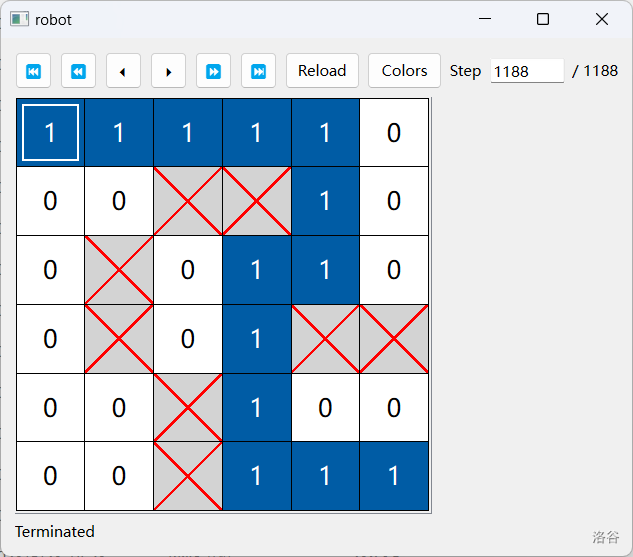
我们要干的事是将一棵树删空。当我们访问到一个结点 的时候,我们先依次访问 的所有儿子 并将 的子树删空,然后再删掉 并回到 ,继续删除 其他儿子的子树。用 的语言,我们从 倒着走回 ,将一路上所有的 改成 。当一个 被从 改成 时,我们开始清理 的子树。当 Pulibot 站在一个 或者一个箭头上时,如果 的儿子已经都变成了 ,那么就将 也改成 并走回 ;如果 的儿子中还有指向 的箭头 ,那么直接走到 。
有一个细节问题在于如果最短路上的一个 有一些儿子已经变成了 ,那么需要重新把这些 指向这个 才能继续进行下去。好在之前的所有讨论中都不会出现 Pulibot 站在一个 上而 个邻居中有 的情况,所以直接让 Pulibot 走到这个 并将这个 指向那个 即可。
代码实现:https://loj.ac/s/1880747。可以获得 分。
- 1
信息
- ID
- 9186
- 时间
- 1000ms
- 内存
- 2048MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
