自动搬运

查看原文

来自洛谷，原作者为

	teylnol_evteyl 我是狸猫盘的猫 | 哇，Teylnol Evteyl！ | 很慢地摇头

搬运于2025-08-24 22:49:57，当前版本为作者最后更新于2023-09-04 16:11:48，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这篇题解中，我将从线段树的角度重新讲解，同时提出一个扩展。

我们可以用权值线段树维护最长连续段：线段树每个节点维护 $L,R,M,S$ 分别表示这个区间的左边连续段长度、右边连续段长度、最大连续段长度、区间长度，这样就可以实现区间合并。

这样建的线段树如图：

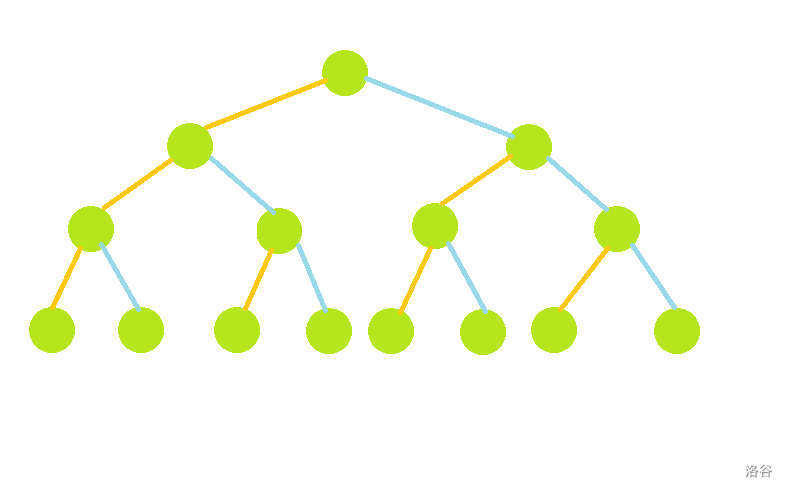
其中橙色线段代表左儿子，蓝色线段代表右儿子，下同。

为了方便后文叙述，“层”从下往上、从 $0$ 开始编号，层的最大编号为 $k$，每一层的节点从 $0$ 开始编号。

考虑一个异或 $x$ 的操作，比如 $x=5$，如果固定底层的节点不变，则线段树会长这个样子：

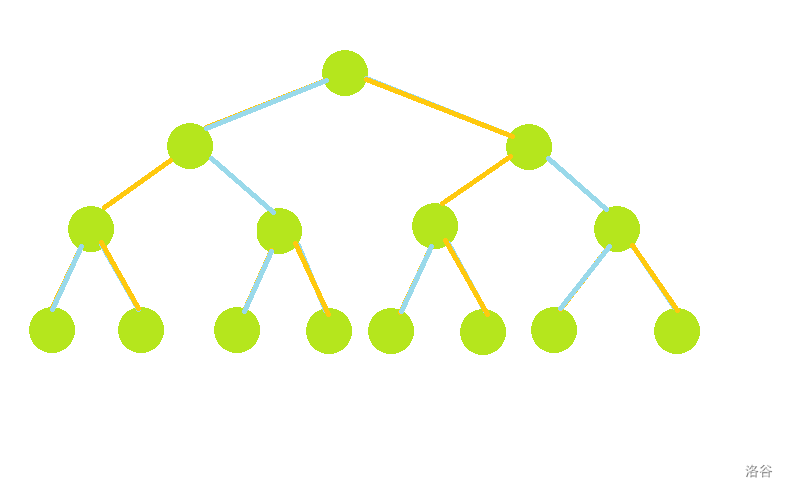
可以发现，实际上是把第 $1$ 层和第 $3$ 层的节点交换左右儿子。

实际上，对于异或 $x$ 的操作，若 $x$ 二进制第 $i$ 位（从低到高，从 $0$ 开始编号）为 $1$，则将线段树第 $i+1$ 层的左右儿子交换。

对于所有的异或 $x$ 的操作，线段树的节点会有很多重合部分，把所有的操作的线段树建出来并合并，则会是这个样子：

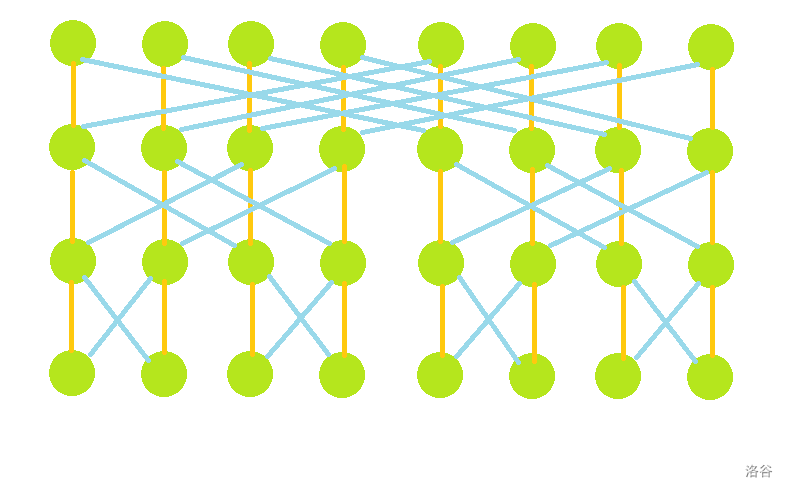
有几个性质：

• 对于第 $i(i>0)$ 层第 $j$ 个节点，它的左儿子是第 $i-1$ 层第 $j$ 个节点，右儿子是第 $i-1$ 层第 $j\bigoplus 2^i$ 个节点，其中 $a\bigoplus b$ 表示 $a$ 和 $b$ 的按位异或。
• 对于第 $k$ 层第 $j$ 个节点，以这个点为根的线段树是异或 $j$ 操作后的线段树。

对于本题，第 $k$ 层节点的 $M$ 值便是答案。

实际上，由于是线段树，它可以维护区间合并。也就是说，下标异或的背景下，可以 $O(\log n)$ 求一般的可以区间合并的区间查询，但不支持快速修改（如图，一个底层节点涉及的节点是 $O(n)$ 的）。

比如有以下问题：

• 这题的基础上可以加一个值域区间的限制。
• 给定长度为 $2^m$ 的序列 $a$，$q$ 次询问给定 $l,r,x$ 求 $\max_{i=l}^r a_{i\bigoplus x}$，$1\leq m \leq 20$，$1\leq q \leq 2^{20}$，$0\leq a_i\leq 10^9$。
• 给定大小为 $n$ 的集合 $a$，$q$ 次询问给定 $x,k$，求 $a$ 里的数异或上 $x$ 后，集合的第 $k$ 小值，$1\leq n,q \leq 2^{20}$，$0\leq a_i\leq 2^{20}$。

#include <bits/stdc++.h>

using namespace std;

const int M = 21, N = 1 << 19 | 5;

int m = 19, n = 1 << m, q, t, x, y;
struct node{
	int l, r, m, p;
}s[2][N];

void pushup(node &u, node &l, node &r)
{
	u.l = l.p ? l.l + r.l : l.l;
	u.r = r.p ? r.r + l.r : r.r;
	u.m = max(l.r + r.l, max(l.m, r.m));
	u.p = l.p & r.p;
}

int main()
{
	scanf("%d%d", &q, &t);
	while(q -- ) scanf("%d", &x), s[0][x] = {1, 1, 1, 1};
	for(int i = 1, x = 1, y = 0; i <= m; i ++ , x ^= 1, y ^= 1)
		for(int j = 0; j < n; j ++ )
			pushup(s[x][j], s[y][j], s[y][j ^ (1 << i - 1)]);
	while(t -- ) scanf("%d", &x), y ^= x, printf("%d\n", s[1][y].m);
	return 0;
}