自动搬运

查看原文

来自洛谷，原作者为

	One_JuRuo 没实力的只会切水题的超级大蒟蒻

搬运于2025-08-24 22:49:39，当前版本为作者最后更新于2023-08-18 21:01:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

思路

刚看到还被吓了一跳，以为又是什么神仙题目，细想了一下觉得有做头。

Step1.不算很好的解法

首先想到左下一个右上一个，就可以套一圈，然后就可以先套一个正方形出来，这个正方形可以尽可能的大，如下图的红色框。

然后就剩下三种情况：

1. 刚好覆盖完（即黑色方格恰好在正中间），输出就完事儿。
2. 留下两边，直接对角输出就完事儿，剩多少就输出多少。
3. 留下三边，这样就剩下两个对角，先从一个对角输出，然后从另一个对角输出。

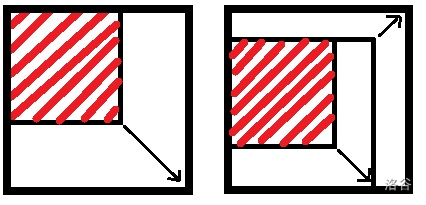
如上图，红色方格代表套出的正方形，左侧为第二种情况，右侧为第三种情况。

想法很不错（至少当时我是这么觉得的），然后实现了很久，居然 WA 了。

对了，顺带一提，设套出的正方形边长为 $k$，再令 $sum=\frac{k-1}{2}$，那么套出的正方形有 $2\times sum$ 个 L 形，还剩下 $n-2\times sum-1$ 个空行或者空列，也就是还剩下 $n-2\times sum-1$ 个 L 形。

所以一共会放 $n-1$ 个 L 形。

如果想看这个做法的代码，很抱歉，我实在不想去调了，想看可以看这个屎山代码。

Step2.逐步扩展的正方形

抛弃了上面的做法后，我就跑去看其他题了，然后突然就想到了一个很不错的方法。

倒过来想，我们如何把一个完整的正方形通过切割 L 形，变成只有 $1\times 1$ 的黑色方格呢？

可以每次从边角切一个 L 形，就变成了一个边长小 $1$ 的小正方形，然后逐步朝黑色方格切割，最后就可以边长黑色方格。

我们再反过来，每次从当前正方形的四个角添一个正方形就可以了，直到添成 $n\times n$ 的大正方形。

每次边长大 $1$，所以需要 $n-1$ 次，这个方法的总次数比上一个方法好理解一些。

AC 代码

#include<bits/stdc++.h>
using namespace std;
int n,x,y,xx,xxx,yy,yyy;
int main()
{
	scanf("%d%d%d",&n,&x,&y);
	printf("Yes\n%d\n",n-1);//直接得出答案
	xx=xxx=x,yy=yyy=y;//记录边界，用xx，xxx之类的绝对不是因为x1,x2,y1,y2是关键字CE了qwq
	for(int i=1;i<n;++i)
	{
		if(xx>1&&yy>1) printf("%d %d %d %d\n",--xx,--yy,i,i);//如果可以从这个方向添L形，下面同理
		else if(xx>1&&yyy<n) printf("%d %d %d %d\n",--xx,++yyy,i,-i);
		else if(xxx<n&&yy>1) printf("%d %d %d %d\n",++xxx,--yy,-i,i);
		else printf("%d %d %d %d\n",++xxx,++yyy,-i,-i);
	}
}