自动搬运

查看原文

来自洛谷，原作者为

	czy0323 心之所向，行之所往.

搬运于2025-08-24 22:49:35，当前版本为作者最后更新于2023-08-21 10:16:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

赛时一眼秒（假）了，然后花了 5h 写假做法。

思路 5min，代码 2h，调试 2h，赛后才发现假了qwq

赛时唯一贡献是为队友贡献了 20min 的罚时。

$\textbf{Solution}$

先讲一下我赛时的假思路（因为这对正解很有启发作用）：

统计方案数，考虑 dp。$n \le 10^5$，故 dp 应该是一维的。

令 $f(i)$ 表示选到第 $i$ 条线段为止，第 $i$ 条必选，后面的线段都不选的总方案数。注意到线段的顺序对答案没有影响，我们考虑对所有线段按右端点排序。

很自然的转移方程：

$$f(0) = 1$$ $$f(i) = f(0) + \sum\limits_{1\leq j\lt i,c_i=c_j}f(j) + \sum\limits_{1\leq j\lt i,c_i\neq c_j,r_j\lt l_i}f(j) $$

其中 $c$ 表示颜色数组。

下图是反例（有点丑）：

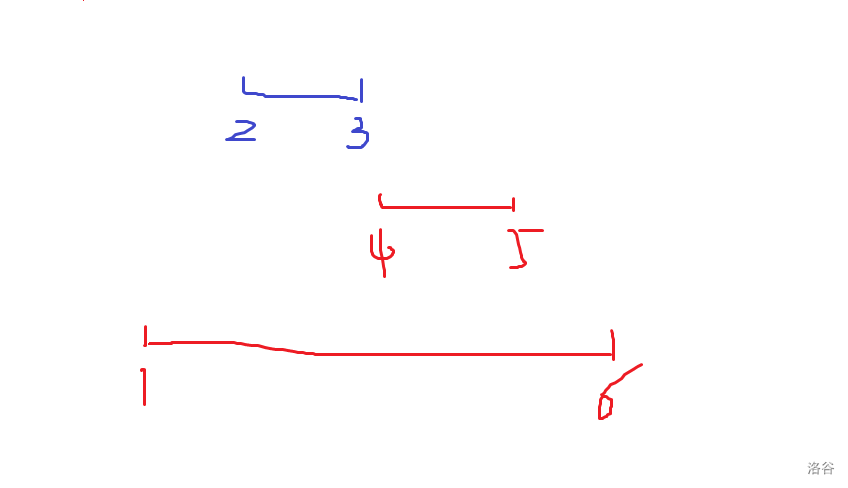
按照我们有的转移方程，$f(3) = 3$，而由定义可知 $f(3)= 2$。

为什么会错呢？因为 $f(3)$ 通过 $f(2)$ 转移过来，$f(2)$ 从 $f(1)$ 转移过来，但其实 $1$ 号线段和 $3$ 号线段不能相容，也就是出现了dp不能转移的情况，所以这种做法就错了。

那怎么做才对呢？

既然由同色线段转移会出现错误，那只由异色线段转移不就行了？

对于 $(i, j) \text{ s.t. }i \lt j , c_i \neq c_j$，我们定义 $cnt(i, j)$：

$$cnt(i, j) = \sum\limits_{i\lt k\lt j,c_j=c_k}[r_i\lt l_k] $$

那么转移方程就是：

$$f(i)=\sum\limits_{1\leq j\lt i,c_i\neq c_j}f(j)\times\sum_{k=0}^{cnt(i,j)}\binom{cnt(i,j)}{k} $$

二项式定理化一下：

$$f(i)=\sum\limits_{1\leq j\lt i,c_i\neq c_j}f(j)\times 2^{cnt(i,j)} $$

时间复杂度 $\mathcal O(n ^ 2)$。

考虑如何优化。

对于一条线段 $i$，由于两种颜色等价，不妨设 $c_i = 0$ 的。

我们需要找到 $\lt l_i$ 的最大 $r_j (\text{s.t. } c_j = 1 )$，即下标 $\le j(\text{s.t. } c_j = 1 )$ 的 $f_j$ 都对 $f_i$ 有贡献。

如果我知道 $\sum\limits_{k\le j, c_k = 1}f(k)\times 2^{cnt(k, i)}$ 就好了。

令 $g_j= \sum\limits_{k\le j, c_k = 1}f(k)\times 2^{cnt(k, i)}$。那 $f_i$ 可以直接由 $g_j$ 转移而来。

那么怎么维护 $g$ 呢？对于当前的 $i, \forall j \text{ s.t. }r_j \lt l_i$ 的 $g_j$ 其实都要被 $\times 2$。由于线段是有序（以右端点为关键字）的，故所有需要更新的 $g_j$ 都在一个连续的区间内。也就是对 $g$ 序列区间乘 $2$。

考虑用一个数据结构维护 $g$。要求：快速查询前缀和、区间乘 $2$ 和单点修改。

显然线段树。由于是单点修改，可以单 Tag。

$\textbf{AC Code}$

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 5, mod = 998244353;
int n, pow2[N], f[N];
int tr[2][4 * N], mark[2][4 * N];	//0红 1蓝 
int ql, qr, d;

struct seg{
	int l, r;
	bool operator <(const seg &b) const{
		return r < b.r;
	}
	bool operator <(const int &d) const{
		return r < d;
	}
};
vector<seg> red, blue;

inline int get(int d, int op){
	if( !op )
		return lower_bound(red.begin(), red.end(), d) - red.begin();
	return lower_bound(blue.begin(), blue.end(), d) - blue.begin();
}

inline int MOD(int a, int b){
	if( a + b >= mod )
		return a + b - mod;
	return a + b;
}

inline void pushdown(int l, int r, int p, int op){
	if( l != r && mark[op][p] ){
		tr[op][p << 1] = tr[op][p << 1] * pow2[mark[op][p]] % mod;
		tr[op][p << 1 | 1] = tr[op][p << 1 | 1] * pow2[mark[op][p]] % mod;
		mark[op][p << 1] += mark[op][p];
		mark[op][p << 1 | 1] += mark[op][p];
		mark[op][p] = 0;
	}
	return;
}

inline void modify(int l, int r, int p, int op, int ope){		//ope0是单点加，ope1是区间乘 
	if( ql <= l && r <= qr ){
		if( !ope )
			tr[op][p] = d;
		else{
			tr[op][p] = MOD(tr[op][p], tr[op][p]);
			mark[op][p]++;
		}
		return;
	}
	pushdown(l, r, p, op);
	int mid = (l + r) >> 1;
	if( ql <= mid )
		modify(l, mid, p << 1, op, ope);
	if( mid < qr )
		modify(mid + 1, r, p << 1 | 1, op, ope);
	tr[op][p] = MOD(tr[op][p << 1], tr[op][p << 1 | 1]);
	return;
}

inline int query(int l, int r, int p, int op){
	if( ql <= l && r <= qr )
		return tr[op][p];
	pushdown(l, r, p, op);
	int mid = (l + r) >> 1, ans = 0;
	if( ql <= mid )
		ans = MOD(ans, query(l, mid, p << 1, op));
	if( mid < qr )
		ans = MOD(ans, query(mid + 1, r, p << 1 | 1, op));
	tr[op][p] = MOD(tr[op][p << 1], tr[op][p << 1 | 1]);
	return ans;
}

signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	
	pow2[0] = 1;
	for(int i = 1; i < N; i++){
		pow2[i] = pow2[i - 1] + pow2[i - 1];
		if( pow2[i] >= mod )	pow2[i] -= mod;
	}
	int T;
	cin >> T;
	while( T-- ){
		for(int i = 1; i <= n; i++)
			f[i] = 0;
		for(int i = 1; i <= 4 * n; i++)
			tr[0][i] = tr[1][i] = mark[0][i] = mark[1][i] = 0;
		red.clear();	blue.clear();
		
		cin >> n;
		for(int i = 1; i <= n; i++){
			seg now;
			int c;
			cin >> now.l >> now.r >> c;
			if( !c )	red.push_back(now);
			else	blue.push_back(now);
		}
		sort(red.begin(), red.end());
		sort(blue.begin(), blue.end());
		
		d = f[0] = 1;
		ql = 0, qr = 0;
		modify(0, red.size(), 1, 0, 0);
		modify(0, blue.size(), 1, 1, 0);
		int p1 = 0, p2 = 0, cnt = 0;
		while( p1 < red.size() || p2 < blue.size() ){
			++cnt;
			if( p1 !=red.size() && (p2 == blue.size() || red[p1].r < blue[p2].r) ){		//选红色线段
				ql = 0, qr = get(red[p1].l, 1);
				d = f[cnt] = query(0, blue.size(), 1, 1);
				modify(0, blue.size(), 1, 1, 1);
				ql = qr = p1 + 1;
				modify(0, red.size(), 1, 0, 0);
				p1++;
			}
			else{
				ql = 0, qr = get(blue[p2].l, 0);
				d = f[cnt] = query(0, red.size(), 1, 0);
				modify(0, red.size(), 1, 0, 1);
				ql = qr = p2 + 1;
				modify(0, blue.size(), 1, 1, 0);
				p2++;
			}
		}
		
		int ans = 0;
		for(int i = 0; i <= n; i++)
			ans = MOD(ans, f[i]); 
		cout << ans << "\n";
	}
	return 0;
}

LaTeX：@Matrix_mlt