自动搬运

查看原文

来自洛谷，原作者为

	yanxiashi 总是这样

搬运于2025-08-24 22:49:26，当前版本为作者最后更新于2023-08-16 16:59:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

原题链接

我是蒟蒻，T1 是简单的贪心、黄题的样子，但是被卡了好久才推出来。所以写个题解加深印象。

如果有问题尽管提出，觉得不错的大佬们请点个赞呗~。

特别鸣谢

题意（抽象向）

一个 $n\times m$ 的矩形 $A$（空地）中有一个 $x\times y$ 的小矩形 $B$ （雨伞）。对矩形 $A$ 任意地撒点，每次（天）撒 $k$ 个，并返回是否落到矩形 $B$ 内，问至少需要多少天、多少雨滴才能确定一个小矩形 $B$。

思路（逐步向）

主要思想：贪心。

本题有两个任务，一是求出最少的雨点数 $Rain$，二是求出最少的天数 $Day$（天数比雨点数好求，本题为了提升难度把它们倒了一下）。我们先考虑天数怎么求：

天数的求法——

一旦知晓最少雨滴数，只要每天都尽可能地多下雨，那么天数一定是最小的。（贪心）

于是求最少天数的函数呼之欲出：

LL Get_Day(LL k,LL Rain){
  if(Rain % k == 0) return Rain / k;
  //正好下完
  else return (LL)Rain / k + 1;
  //多一天处理余数
}

雨滴数的求法——

最少雨滴数怎么求呢？根据题意，我们需要让一些雨点排除一个雨伞的位置。那么有没有一种可能，我们可以用一个雨滴、排除一个雨伞的位置呢？有！

举个例子，当 $n=7,m=7,x=3,y=2$ 时，我们可以像图片中的那样把 $7\times 7$ 的空地最大地划成 $6$ 个 $2\times 3$ 的小矩形。右边和下面的两条的边界划分不出矩形，我们将其排除在外。

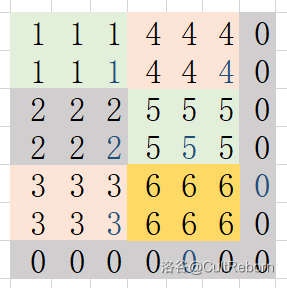
接着，我们在每个小矩形和两条边界中落雨，排除出一个的标号为 $6$ 的矩形（其实其它的标号也行），它，就是我们所求得的雨伞。可以证明最少的雨点数就是 $可以划分的矩形数-1+边界数$。（贪心）

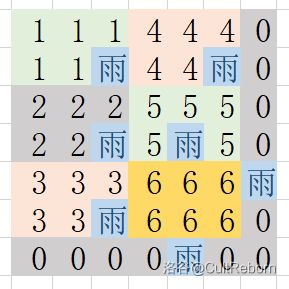
可以划分的矩形数为 $n \div x \times (m \div y)$。边界数随情况而定，只要计算一下 $n\bmod x$ 和 $m\bmod y$，判断一下右边界和下边界存不存在就好了。

代码如下：

LL Get_Rain(LL n,LL m,LL x,LL y){
  if(n % x == 0 && m % y == 0)
  //没有边界
    return n / x * (m / y) - 1;  
  if(n % x == 0 && m % y != 0)
  //有一个下边界
    return n / x * (m / y);
  if(n % x != 0 && m % y == 0)
  //有一个右边界
    return n / x * (m / y);    	  
  return n / x * (m / y) + 1;
  //有两个边界
}

代码（丑陋向）

注意一些细节：

1. 开 long long。
2. 雨伞不能旋转，所以 $n$ 严格对应 $x$，$m$ 严格对应 $y$。
3. 本题的思路来源：第三个样例中 $(214\div3)\times(748\div64)+1=782$。所以找规律一定是做题的基本艺能。

使用了贪心思想，时间复杂度为 $O(1)$。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
LL Get_Rain(LL n,LL m,LL x,LL y){
  if(n % x == 0 && m % y == 0)
    return n / x * (m / y) - 1;
  if(n % x == 0 && m % y != 0)
    return n / x * (m / y);
  if(n % x != 0 && m % y == 0)
    return n / x * (m / y);
  return n / x * (m / y) + 1;
}
LL Get_Day(LL k,LL Rain){
  if(Rain % k == 0) return Rain / k;
  else return (LL)Rain / k + 1;
}
signed main(){
  LL n,m,x,y,k;	
  scanf("%lld %lld %lld %lld %lld",
  &n,&m,&x,&y,&k);
  LL Rain = Get_Rain(n,m,x,y);
  LL Day = Get_Day(k,Rain);
  printf("%lld %lld",Day,Rain);
  return 0;
}

终于看完了！觉得不错请点个赞吧！！！