1 条题解
-
0
自动搬运
来自洛谷,原作者为

AFewSuns
弱省弱校蒟蒻,tcl,zbl搬运于
2025-08-24 22:49:24,当前版本为作者最后更新于2023-09-04 11:49:02,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题目大意
有一棵 个点的树,每个节点上有一种药材,可用三元组 表示。
若你获得了 种属性分别为 的药材,你可以任取 个非负实数 ,配置出 的药剂。
你要选取树上的一个连通块,用连通块上的药材配置出 的药剂,求可以配置出此药剂的连通块大小的最小值,或判断无解。
保证所有 。
题目分析
首先注意到所有的 ,那么相当于 ,只需要使得前两个元素相等即可。
只保留每个点的 ,将其视作平面上的点。当有两个点时,它们能配出线段上的任意点;当有三个点时,它们能配出三角形中的任意点;以此类推, 个点就能配出它们凸包中的任意点,而判断是否可行就相当于判断 这个点在不在凸包内部。
为了方便,先将 平移至原点,再将其他点缩放到单位圆上,容易证明这并不影响原点在凸包内的判断。接下来证明几个简单的性质:
1. 凸包包含原点 存在三个点的三角形包含原点
充分性显而易见,只需证明必要性。
选取圆上夹角最大的两个点 ,分别过原点作直线交圆的另一端于 ,如果不存在三角形包含原点,那么就不能有点在 圆弧内,同时因为 夹角最大,所以不能有点在 圆弧内,于是所有点都在 圆弧内,凸包不包含原点。
2. 凸包包含原点 每个点都能找到另外两个点构成的三角形包含原点
首先由上面可得一定存在某个三角形包含原点,不妨设这个三角形为 。
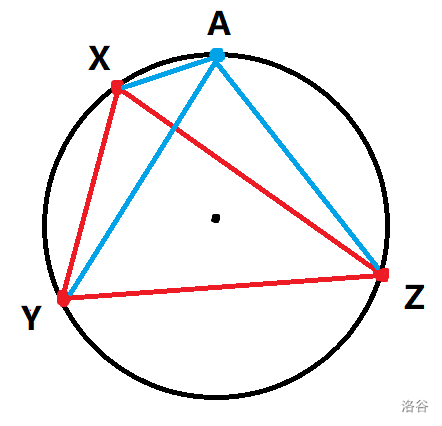
对于任意一点 ,由于三角形 和 的并完全包含三角形 ,所以三角形 和 之间必有一个包含原点。
3.可能成为答案的连通块一定是一条链
如果连通块不是一条链,由于存在三个点包含原点,那么一定形如以下结构:
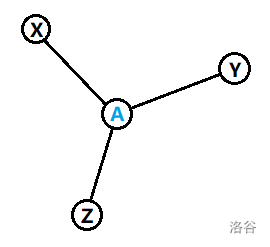
其中包含原点的三角形 限制了连通块大小, 为它们的交点。那么仿照上面的证明, 三个三角形之间必有一个包含原点,无论哪一个都比之前的连通块优,并且都是链。
注:上面的证明均不考虑一个点、两个点的情况。
接下来考虑点分治,设当前分治重心为 ,那么只需要计算链跨过 的情况。分两种情况讨论:
1. 链的两端在不同子树内
设链的两端为 , 对应的点分别为 ,那么如下图:
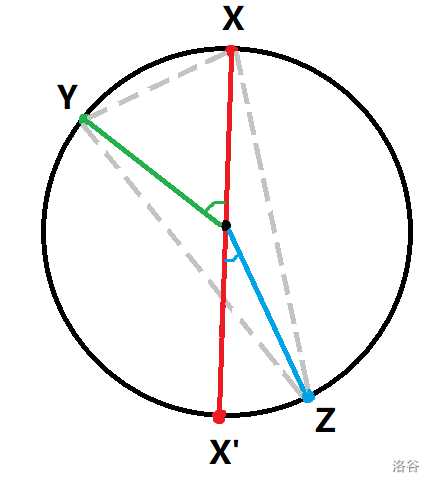
不妨设 在左边, 在右边,那么三角形 包含原点等价于 $\mathop{XY}\limits^{\frown} \geq \mathop{X'Z}\limits^{\frown}$。将每个点按照左右两边分类,按弧长排序后双指针即可做到 。
由于连通块大小等于 ,只与深度有关,所以可以对每个深度维护左边部分最大值和右边部分最小值,做一遍前缀最大值/最小值后双指针,时间复杂度 。
2. 链的一端为
直接在 dfs 的过程中维护 到当前点的路径上,左边部分最大值和右边部分最小值,根据当前点在哪边来判断是否可行。
总时间复杂度 。
代码
随便写的,目前最优解 269ms。
弧长的比较可以转化为角度,用点积比较。
#include<bits/stdc++.h> using namespace std; using namespace my_std; #define eps 1e-12 ll n,head[50050],cnt=0,ans=inf; ll rt,minn=inf,rsiz,siz[50050],maxdep; db L[50050],R[50050]; bl ck[50050]; struct edge{ ll nxt,to; }e[100010]; struct point{ db x,y; }a[50050],X,XX; il void add(ll u,ll v){ e[++cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt; } il db cross(point x,point y){ return x.x*y.y-x.y*y.x; } void getroot(ll fa,ll u){ siz[u]=1; ll maxx=0; go(u){ ll v=e[i].to; if(v==fa||ck[v]) continue; getroot(u,v); siz[u]+=siz[v]; maxx=max(maxx,siz[v]); } maxx=max(maxx,rsiz-siz[u]); if(minn>maxx){ minn=maxx; rt=u; } } void dfs(ll fa,ll u,ll dep,db lft,db rgt){ siz[u]=1; maxdep=max(maxdep,dep); if(fabs(XX.x-a[u].x)<eps&&fabs(XX.y-a[u].y)<eps) ans=min(ans,dep+1); else if(cross(X,a[u])>eps){ db tmp=-(X.x*a[u].x+X.y*a[u].y); if(rgt<=tmp) ans=min(ans,dep+1); lft=max(lft,tmp); L[dep]=max(L[dep],tmp); } else if(cross(X,a[u])<-eps){ db tmp=-(XX.x*a[u].x+XX.y*a[u].y); if(lft>=tmp) ans=min(ans,dep+1); rgt=min(rgt,tmp); R[dep]=min(R[dep],tmp); } go(u){ ll v=e[i].to; if(v==fa||ck[v]) continue; dfs(u,v,dep+1,lft,rgt); siz[u]+=siz[v]; } } void solve(ll u){ ck[u]=1; X=a[u]; XX=(point){-a[u].x,-a[u].y}; maxdep=0; dfs(0,u,0,-inf,inf); L[0]=-inf; R[0]=inf; fr(i,1,maxdep) L[i]=max(L[i],L[i-1]); fr(i,1,maxdep) R[i]=min(R[i],R[i-1]); ll now=maxdep+1; fr(i,1,maxdep){ while(R[now-1]<=L[i]) now--; if(now<=maxdep) ans=min(ans,i+now+1); } fr(i,1,maxdep) L[i]=-inf; fr(i,1,maxdep) R[i]=inf; go(u){ ll v=e[i].to; if(ck[v]) continue; rsiz=siz[v]; minn=inf; getroot(u,v); solve(rt); } } int main(){ n=read(); fr(i,0,n){ a[i].x=read(); a[i].y=read(); ll tmp=read(); } fr(i,1,n){ a[i].x-=a[0].x; a[i].y-=a[0].y; } fr(i,2,n){ ll u=read(),v=read(); add(u,v); add(v,u); } fr(i,1,n){ db len=sqrt(a[i].x*a[i].x+a[i].y*a[i].y); if(fabs(len)<eps){ write(1); return 0; } a[i].x/=len; a[i].y/=len; } rsiz=n; minn=inf; getroot(0,1); fr(i,1,n) L[i]=-inf; fr(i,1,n) R[i]=inf; solve(rt); if(ans==inf) write(-1); else write(ans); }
- 1
信息
- ID
- 9086
- 时间
- 4000ms
- 内存
- 1024MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
