自动搬运

查看原文

来自洛谷，原作者为

	1qaz234567pzy AFO

搬运于2025-08-24 22:49:14，当前版本为作者最后更新于2023-08-18 09:06:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一道交互好题恶心题

感谢 Aaronwrq 大佬的帮助，题解有所借鉴 Jason0211 的题解。

思路

我们可以把每个串看成一个集合，所以总共有 $m$ 个集合，对于每个团子，我们尝试将其插入某个集合中。插入时需要维护以下性质：

一：每个集合内的每个团子的颜色互不相同。

二：同一种颜色的团子是按串串的编号从左到右放到每个串串中的。

所以现在问题变为了如何检验这个颜色的团子放在哪里。

而我们似乎只能用 Query(x[]) 函数来检验，但是我们总共只能调用 $50000$ 次 Query(x[]) 函数。而团子的总数最多有 $m \times n$ 即 $10000$ 个。所以我们需要在最多调用 $5$ 次 Query(x[]) 函数的情况下来求出这个团子放在哪。

我们根据这些想到可以二分，因为根据性质二，这种颜色的团子一定是前面一段串串有，后面的串串全部都没有的，所以可以通过二分的方式来查找。而二分要调用大约 $\log_2 25$ 次 Query(x[]) 函数，而 $4 \le \log_2 25 \le 5$，刚好小于等于 $5$，所以我们接下来就要考虑怎么二分了。

我们先假设前几个串串上已经有了一些团子，就像这样：

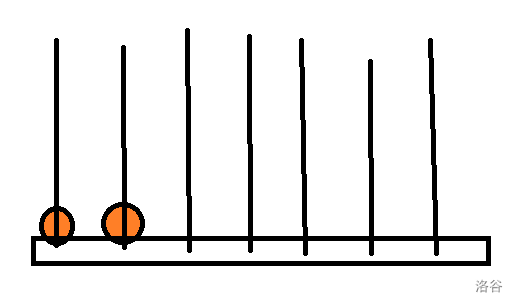
那么对于下一个这种颜色的团子，如果我们放在这两个已经有这种颜色的串上，就像这样：

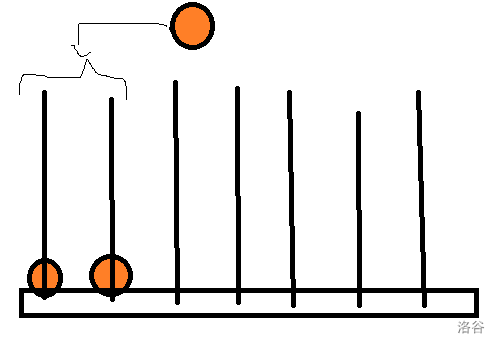
由于这种颜色的团子的个数等于总的串串数，所以如果我们放在这两个已经有这种颜色的串上的话，所有剩下的团子就没有办法组成剩下串串的个数个一流团子串。（建议自己在纸上画一下）欸，这不就可以用到 Query(x[]) 函数了吗！

我们设当前的团子放在第 $mid$ 个串上，那么如果所有没有处理的团子和第 $mid+1$ 到第 $m$ 个串上的所有团子加起来能做出至少 $m-mid$ 个一流团子串的话，这个团子就可以放在第 $mid$ 个串上。就像这样（能放的情况）：

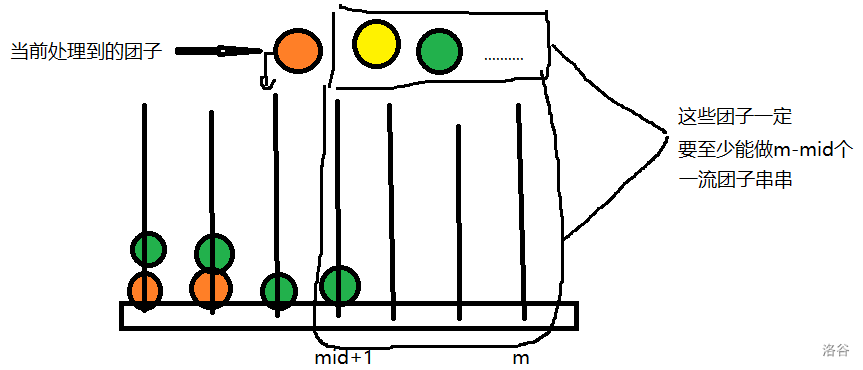
我们就用这个进行二分，如果能做出至少 $m-mid$ 个一流团子串，我们就把 $r$ 赋值为 $mid-1$，同时用 $ans$ 记录下 $mid$，否则就把 $l$ 赋值为 $mid+1$，二分的边界条件为 $l \le r$。（至于为什么这么二分，读者可以自己研究一下）二分完后就把这个团子放入第 $ans$ 个串串中。把每个团子都这样处理后这道题就做完了。

核心代码如下：

//注意是交互题
namespace {

    int n,m;
    vector<int> v[1000];
}  
bool work(int h,int j)
{
	vector<int> G;
    for(int qqq=h+1;qqq<=n*m;qqq++)
    {
        G.push_back(qqq);
    }
    for(int qqq=j+1;qqq<=m;qqq++)
    {
        for(int qq=0;qq<v[qqq].size();qq++)
        {
            G.push_back(v[qqq][qq]);
        }
    }
    return Query(G)>=m-j;
}
void Solve(int N, int M) 
{
    n=N;
    m=M;
    for(int qqq=1;qqq<=n*m;qqq++)
    {
        int ll=1,rr=m,mid,ans=-1;
        while(ll<=rr)
        {
            mid=(ll+rr)>>1;   
			int www=work(qqq,mid);     	
            if(www)
            { 	
				 rr=mid-1;
                ans=mid;//记录mid
            }
            else
            {
                ll=mid+1;
            }
        }
        v[ans].push_back(qqq);
    }
    for(int qqq=1;qqq<=m;qqq++)
    {
        Answer(v[qqq]);
    }
}

AC记录