自动搬运

查看原文

来自洛谷，原作者为

	Po7ed **

搬运于2025-08-24 22:49:13，当前版本为作者最后更新于2024-05-06 14:13:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目传送门

以下设 $\operatorname{dis}(x,y)$ 表示树上 $x,y$ 两点间的距离。修改时对 $u$ 的周围与 $u$ 距离小于等于 $d$ 的点的点权乘 $w$。

暴力不行，于是考虑打标记。

注意到 $0\le d\le 40$，一个很自然的想法是：设 $tag(x,i)$ 表示将 $x$ 的子树内与 $x$ 距离小于等于 $i$ 的所有点的点权乘 $tag(x,i)$。修改时遍历 $l$ 分别表示 $u$、$u$ 的父亲……$u$ 的 $d$ 级祖先，将 $tag(l,d-\operatorname{dis}(u,l))$ 都乘上 $w$ 即可。查询时依然遍历 $l$，沿途把标记累乘即可。这样 $l$ 最多 $O(d)$ 个取值，总时间复杂度是 $O(nd)$ 的。

显然这样会有点权被重复乘 $w$，解决方案也很简单，打标记时将重复的用除法抵消。具体的，设 $l$ 的一个孩子 $s$，使 $s$ 的子树内有 $u$，打标记时将 $tag(s,d-\operatorname{dis}(u,l)-1)$ 即 $tag(s,d-\operatorname{dis}(u,s)-2)$ 除以 $w$ 即可。

下图给出了一个例子帮助理解：

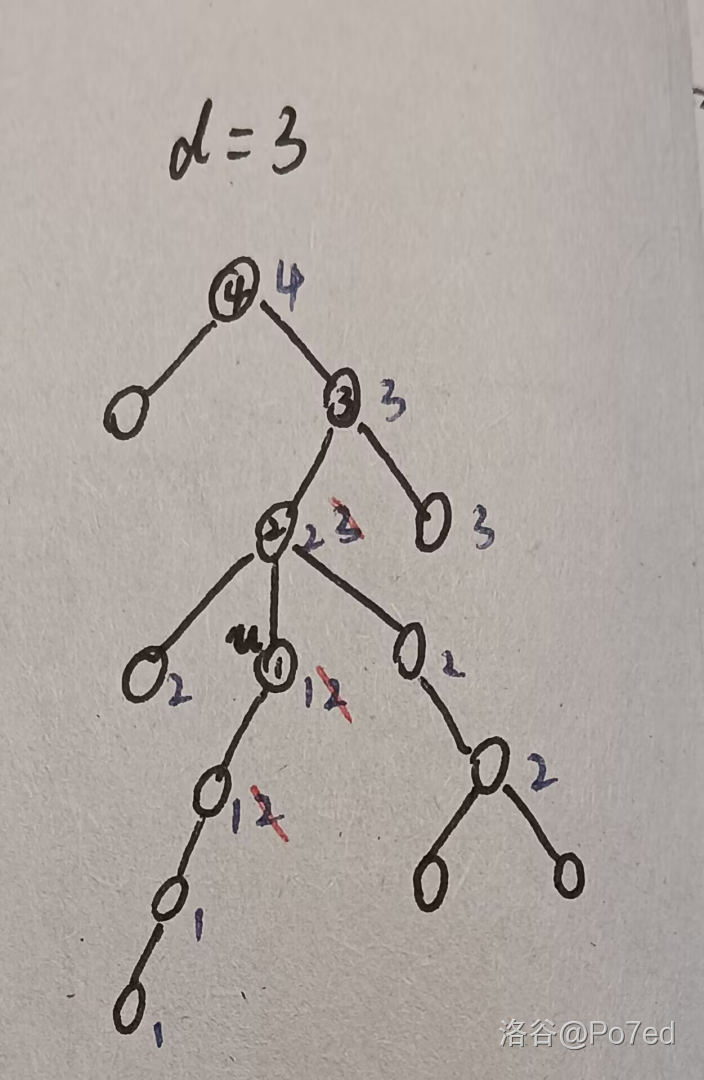
图中 $1$ 号点（即 $u$）将它自己和它下面的 $3$ 个点乘了 $w$，$2$ 号点也将其子树内的 $5$ 个点乘 $w$，但 $1$ 号点由于被重复乘，通过除法被消去了一次。同理，$3$ 号乘了 $3$ 个点，其中 $2$ 号点被消去了一次。$4$ 号乘了它自己。这样每个需要乘的点都刚好被乘了一次。

但模数可能没有逆元，这样做还是不行。

不妨换个角度，观察到 $l$ 可以取到 $s$，即对于 $s$ 的标记的操作，事实上是 $tag(s,d-\operatorname{dis}(u,s))$ 乘 $w$，$tag(s,d-\operatorname{dis}(u,s)-2)$ 除以 $w$。

考虑对标记的定义稍作修改，设 $tag'(x,i)$ 表示将 $x$ 的子树内与 $x$ 距离刚好等于 $i$ 的所有点的点权乘 $tag'(x,i)$，则上面对 $s$ 的标记的操作等价于 $tag'(s,d-\operatorname{dis}(u,s)-1)$ 和 $tag'(s,d-\operatorname{dis}(u,s))$ 都乘 $w$。我们成功地将一乘一除转化为了两个乘。（有点类似前缀和的还原。）对应到上图的例子，就是换一个乘 $w$ 消：

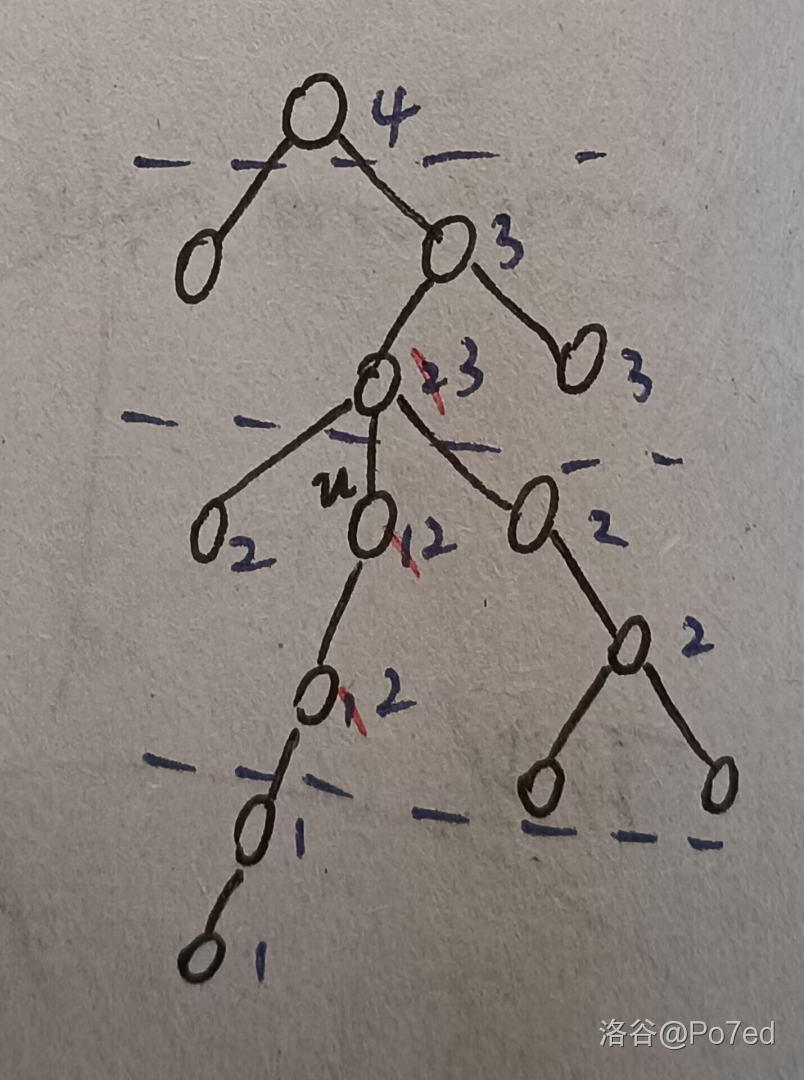
这样，时间复杂度依然是 $O(nd)$ 的，询问时还是直接跳祖先乘标记。

代码：

#include <iostream>
#include <vector>

const int N=214514,D=100;
int n,m,mod;
int a[N];
int tag[N][D],fa[N];
std::vector<int> e[N];

void dfs(int u,int f=0)
{
	fa[u]=f;
	for(int v:e[u])if(v!=f)dfs(v,u);
}

int main()
{
	scanf("%d %d",&n,&mod);
	int u,v;
	for(int i=1;i<n;i++)
	{
		scanf("%d %d",&u,&v);
		e[u].push_back(v);
		e[v].push_back(u);
	}
	dfs(1);
	for(int i=1;i<=n;i++)scanf("%d",a+i);
	for(int i=1;i<=n;i++)for(int j=0;j<=40;j++)tag[i][j]=1;
	scanf("%d",&m);
	int o,x,d,w;
	while(m--)
	{
		scanf("%d %d",&o,&x);
		if(o==1)
		{
			scanf("%d %d",&d,&w);
			while(d>=0&&x)
			{
				tag[x][d]=1ll*tag[x][d]*w%mod;
				if(d>=1)tag[x][d-1]=1ll*tag[x][d-1]*w%mod;
				if(x==1) // 根节点要特判，因为根节点没有祖先抵消
				{
					for(int i=0;i<=d-2;i++)tag[1][i]=1ll*tag[1][i]*w%mod;
					break;
				}
				x=fa[x];
				d--;
			}
		}
		else
		{
			int ans=a[x];
			for(d=0;d<=40;d++) // 跳父亲累乘 tag
			{
				if(!x)break;
				ans=1ll*ans*tag[x][d]%mod;
				x=fa[x];
			}
			printf("%d\n",ans);
		}
	}
	return 0;
}