1 条题解
-
0
自动搬运
来自洛谷,原作者为

Y_B_X
...搬运于
2025-08-24 22:48:57,当前版本为作者最后更新于2023-08-09 18:18:48,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题意:求满足 $\sum\limits_{k=0}^{n-1}\prod\limits_{j=0}^{m-1}a_{(k+j)\bmod n}=k,\forall_{i\in[0,n)}\ a_{i}=\pm 1$ 的 的数量。
。为方便考虑,以下下标均自动对 取模, 指异或, 指异或和。
重新设 ,并将限制条件改为 $\sum\limits_{k=0}^{n-1}(-1)^{\bigoplus \limits_{0\leq j<m}A_{k+j}}=k$。
首先考虑 怎么做,此时 ,设 的 的个数为 ,则有 ,所以 ( 不是偶数时答案必为 )。那这时答案显然为 。
对于一般情况,设 ,则 中 的个数有 个,即 。
考虑统计 的个数,而 由 确定,那接下来要重点做的是便是:
找到每个 能对应的 的数量。
找到关系 中蕴含的 的限制条件。与 的对应关系
假设我们已经有了一个序列 ,考虑如何生成所有满足条件的 。
由于 ,等号右边是确定的,所以当 确定时直接可以推出 。他们间的关系组成了一个长度为 的环,而一共有个 个环。
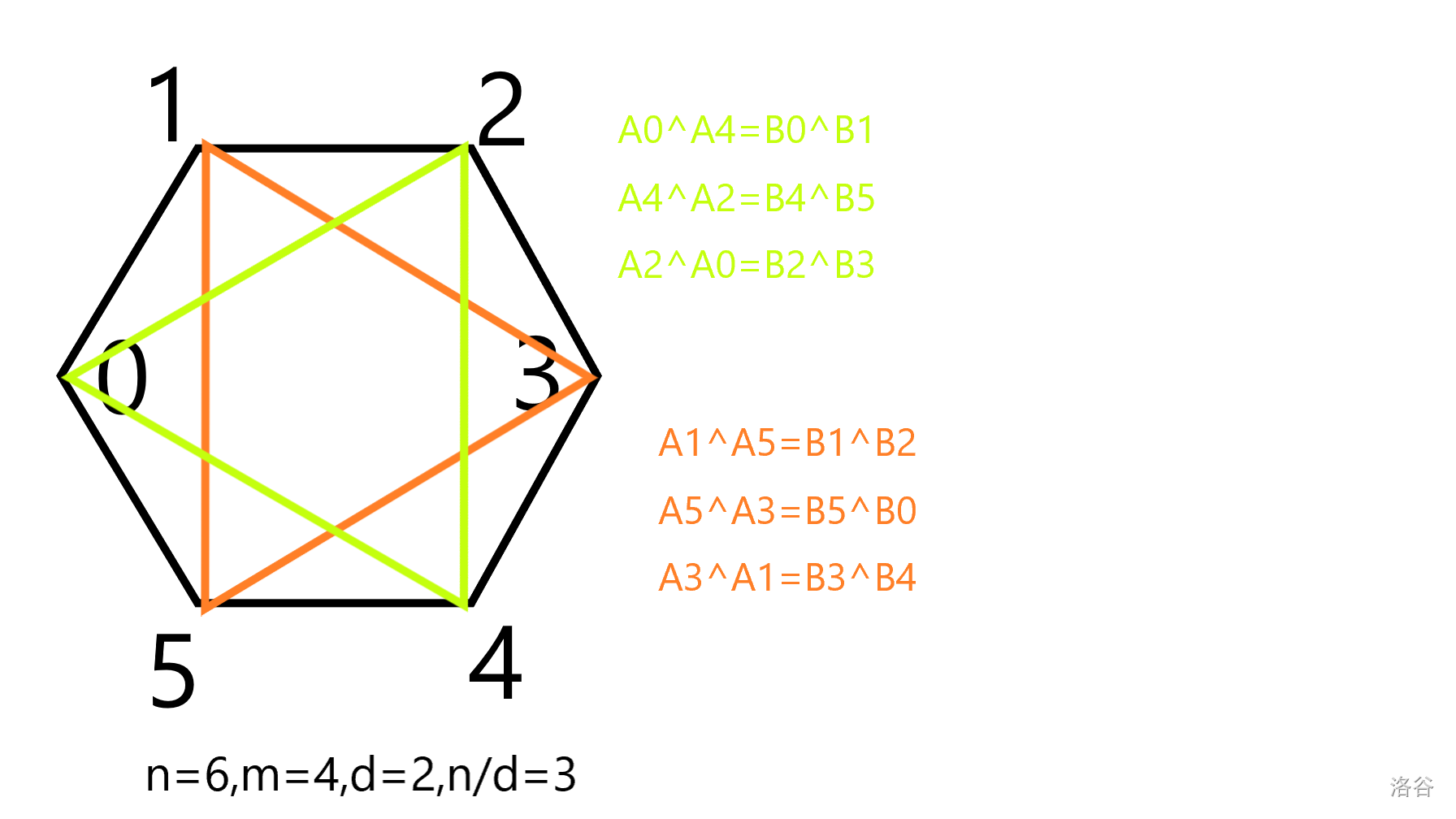
设 ,则我们只需确定 就能得出全部数。
而 等价于 并且 。接下来着重看第二个等式。
由于相差 的倍数的下标之间的关系已经明确,所以 本质上是 等于 个 相异或,再异或上一个已知的数。
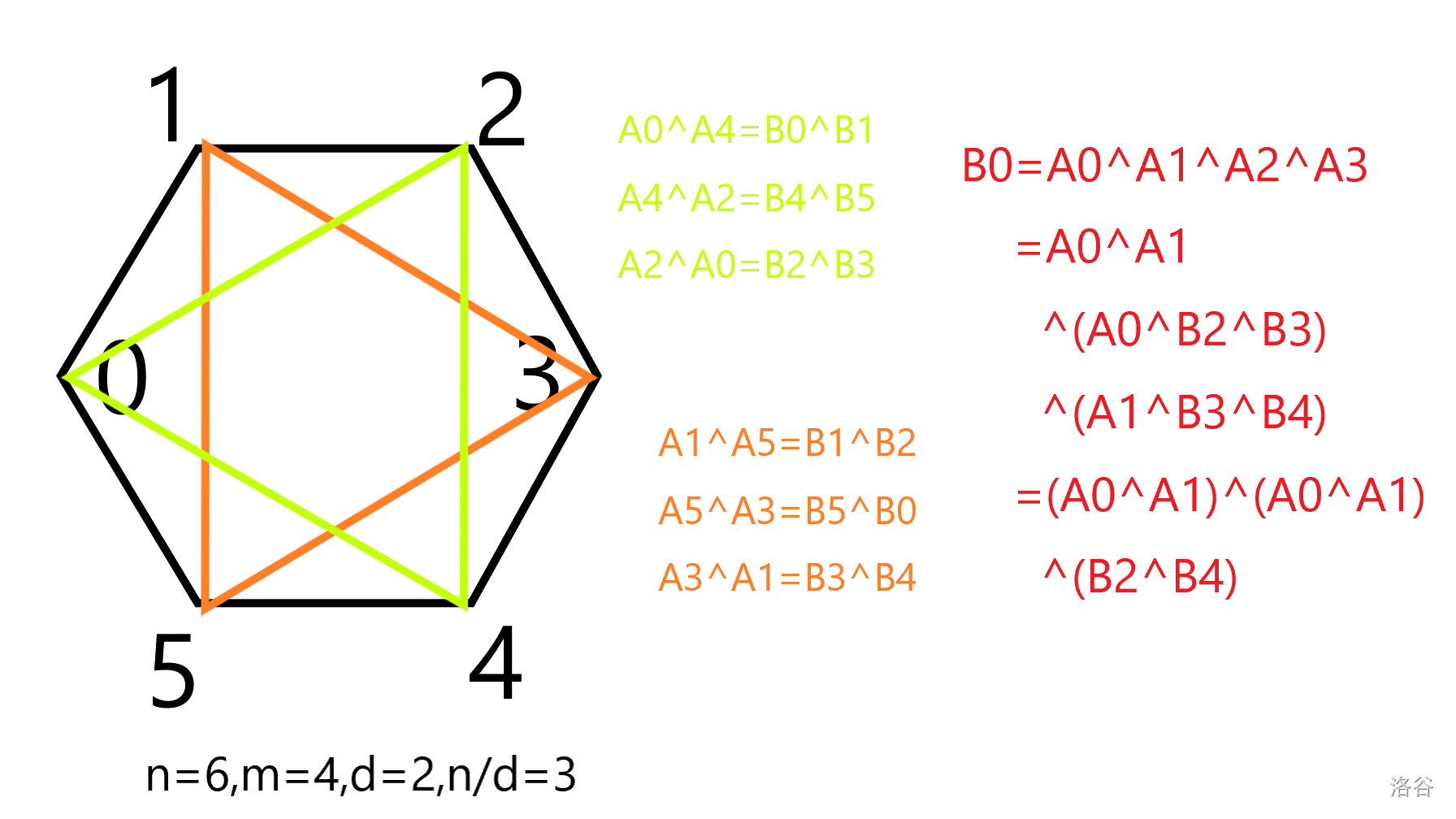
当 是偶数时, 分别出现偶数次,都自己跟自己异或没了,不再有对他们间的限制,方案数为 。
当 是奇数时, 会将明确等于一个数 。由于在所有情况下,所有数异或起来等于 和等于 的方案数相同(改变一个数则一一对应),方案数为 。所以每个 会对应 个 。
的限制条件
对于一个环,相邻两个 间的限制条件是 。但由于这是一个环,将所有这样的关系异或起来后,等号左边的 会变成 (每个数出现两次),所以 $B_{i}\oplus B_{i+1}\oplus B_{i+m}\oplus B_{i+1+m}\oplus \cdots=0$。
设 ,即一个环上所有 的异或和,上面说的就是对所有 都有 ,所以 。于是所有的 要么全部等于 ,要么全部等于 。也就是说每个环上 的和要么全是奇数,要么全是偶数。
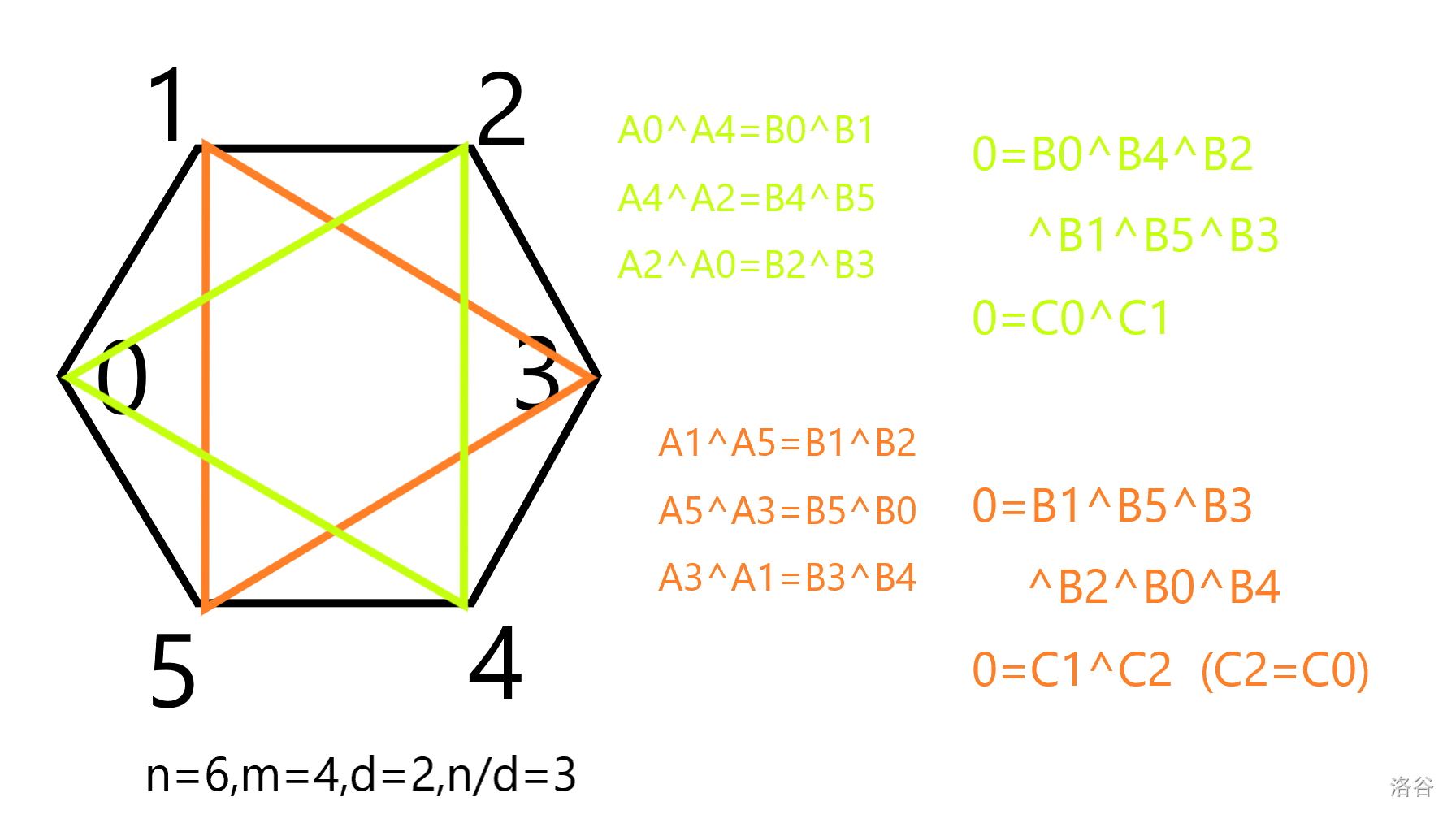
还不止这一限制,依然重新考虑 。
根据之前的讨论,当 是偶数时, 全消掉了,事实上我们能推导出 必定是 ( 的第二张图红字等价于 )。( 是奇数时肯定不会有限制,因为和 有关。)
证明如下:
由于 是偶数,,所以对任意的 , 和 在同一个环内。
为构建 与 间的关系,设 代表从 开始,每次将下标 并对 取模,直到下标为 ,此过程中遍历到的下标上(包括 而不包括 )所有 的异或和,那么就有 (不断由 异或得来)。
所以 $B_{0}=\bigoplus \limits_{0\leq i<m/2}A_i\oplus A_{i+m/2}=\bigoplus \limits_{0\leq i<m/2}S_{i}\oplus S_{i+1}=S_{0}\oplus S_{m/2}$。
考虑一下 是什么,求 过程中遍历的最后一个下标 就是 ,而 又以 结尾(),所以这就是从 开始,不断将下标 ,直到回到 的所有下表标上对应 的异或和,注意 出现了两次,那这就是 。
所以 ,也就是 ,于是 。
设 ,即一个环的长度。
当 是偶数时,每个环上都只能有偶数个 是 , 一共要有 个 ,每个 对应 个 ,所以答案是:
$$2^d[x^p]\left(\sum_{2|i}\binom{t}{i}x^i\right)^d=[x^p]\left((1+x)^{t}+(1-x)^{t}\right)^d $$当 是奇数时,每个环上 的和的奇偶性相同,每个 对应 个 ,答案是:
$$2^{d-1}[x^p]\left(\sum_{2|i}\binom{t}{i}x^i\right)^d+\left(\sum_{2|i+1}\binom{t}{i}x^i\right)^d=[x^p]\dfrac{\left((1+x)^{t}+(1-x)^{t}\right)^d+\left((1+x)^{t}-(1-x)^{t}\right)^d}{2} $$直接 求多项式 次幂, 巨大常数显然过不了。
把他们俩展开,分别有 $\begin{cases}\displaystyle \sum_{i}\binom{d}{i}\sum_{k}\binom{ti}{k}\binom{t(d-i)}{p-k}(-1)^k,m/d\in \mathrm{even}\\\displaystyle \sum_{2|i}\binom{d}{i}\sum_{k}\binom{ti}{k}\binom{t(d-i)}{p-k}(-1)^k,m/d\in \mathrm{odd}\end{cases}$,于是有了 的做法,也不太行。
(这部分解法是参考了题解区的)但由于已经有了封闭形式,多项式的次数不超过 ,按着 的方法,将 补成 的幂 后,对于点值 可以直接快速幂算,单次复杂度 ,而需要的只有一项的系数,可以将点值直接乘上 时的贡献系数得到。
一个小优化:,所以不一定 硬要是 的幂,还可以是 或者 乘上 的某次幂。
这样复杂度是 的,代码:
#include<bits/stdc++.h> #define ll long long using namespace std; const int N=5e6+10; const int mod=998244353; int n,m,p,a,b,ans,nn; int fac[N],ifac[N]; #define sub(x,y) x<y?x-y+mod:x-y inline int qpow(int x,int k){ int res=1; while(k){ if(k&1)res=1ll*res*x%mod; x=1ll*x*x%mod;k>>=1; } return res; } void work(){ int N1=1;while(N1<=n)N1<<=1; int N2=7;while(N2<=n)N2<<=1; int N3=17;while(N3<=n)N3<<=1; int N4=119;while(N4<=n)N4<<=1; int N=min({N1,N2,N3,N4}); p=N-p; int i,w=qpow(3,(mod-1)/N),wp=qpow(w,p),v=1,vp=1,x,y; if((m/b)&1){ for(i=0;i<N;++i,v=1ll*v*w%mod,vp=1ll*vp*wp%mod){ x=qpow(1+v,a);y=qpow(mod+1-v,a); ans=(1ll*(qpow(x+y,b)+qpow(sub(x,y),b))*vp+ans)%mod; } ans=1ll*ans*qpow(N,mod-2)%mod; ans=ans&1?ans+mod>>1:ans>>1; } else { for(i=0;i<N;++i,v=1ll*v*w%mod,vp=1ll*vp*wp%mod){ x=qpow(1+v,a);y=qpow(mod+1-v,a); ans=(1ll*qpow(x+y,b)*vp+ans)%mod; } ans=1ll*ans*qpow(N,mod-2)%mod; } } void main_(){ cin>>n>>m>>p;ans=0; if((n-p)&1)return puts("0"),void(); p=(n-p)>>1; b=__gcd(n,m);a=n/b; work(); cout<<ans<<'\n'; } int main(){ int T;cin>>T; while(T--)main_(); }还没结束,这题实际上能 ,且不依赖于 模数。
回到答案的展开式,后面的求和都是 $\displaystyle \sum_{k}\binom{ti}{k}\binom{t(d-i)}{p-k}(-1)^k$,其中 ,所以 。
于是只需求出所有的 $f_i=\displaystyle \sum_{k}\binom{i}{k}\binom{n-i}{p-k}(-1)^k,0\leq i\leq n$。
这很像范德蒙德卷积,却偏偏多了一个 ,像 等著作也没见着他的影。
但他还是能递推的,可以手搓 得到答案:
$$f_{i+1}=\dfrac{1}{n-i}\left(V f_{i}-Uf_{i-1}i\right) $$ $$V=\dfrac{2n+3n^2+n^3-4p-9np-4n^2p+6p^2+5mp^2-2p^3}{(n-p)^2+3(n-p)+2} $$我真的不信这玩意能有组合意义。推导过程过于复杂,由于篇幅限制就不再展开,有兴趣的看这里。
由于 的解集只能是 , 完全没有那么大,所以不用担心分母为 。
代码没必要放了吧,就一个递推式的事。
最优解到底是怎么回事呢?
- 1
信息
- ID
- 8251
- 时间
- 3000ms
- 内存
- 512MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
