自动搬运

查看原文

来自洛谷，原作者为

	Alex_Wei **

搬运于2025-08-24 22:48:44，当前版本为作者最后更新于2023-08-02 13:25:16，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P9480 [NOI2023] 深搜

超级酷的题目！

思路参考了 Rainbow_qwq 的题解，对他的题解进行一些补充。题解最后给出的代码有：$n\leq 300$ 的性质 B，$n\leq 300$，未卡常正解和卡常后的正解。

首先，$T$ 可以作为 $s$-DFS 树的充要条件是所有非树边均为返祖边，因为 DFS 树的非树边为返祖边，且如果满足条件则对 $T$ 进行 DFS 就是符合条件的 DFS 顺序。

称非树边 $e$ 覆盖 点 $s$ 当且仅当 $e$ 在以 $s$ 为根的 $T$ 上是横叉边（非返祖边）。易知非树边 $e = (u, v)$ 不覆盖 点 $s$ 当且仅当 $s$ 在以 $v$ 为根时 $u$ 的子树内（称为 $u$ 侧），或以 $u$ 为根时 $v$ 的子树内（称为 $v$ 侧）。

对于性质 B，有两种思路：

• 记录从子树内向上延伸的返祖边的最浅深度，并维护当前子树内是否有关键点未被覆盖。
• 设 $c(S)$ 表示不覆盖 $S$ 中任意关键点的非树边数量，设关键点集合为 $U$，容斥得 $\sum_{|S| \geq 1 \ \land \ S\subseteq U} (-1) ^ {|S| + 1} 2 ^ {c(S)}$。

顺着前一种思路不容易解决原问题，因此考虑第二种思路。

非树边的形态

• 称一个点 属于虚树，当且仅当它是虚树的结点。
• 称一个点 落在虚树上，当且仅当它被虚树的某条边覆盖。

定点 $1$ 为根。

建出 $S$ 的虚树 $T_S$。注意要和我们所理解的虚树做区分：当且仅当 $x\in S$ 或有至少三棵子树（包括向上的子树）含属于 $S$ 的点时，$x$ 才属于虚树。它们的唯一区别在于，当 $S$ 所有点的 LCA $d$ 只有两棵子树含属于 $S$ 的点时，$d$ 不属于 $T_S$，但 $d$ 属于我们通常所理解的虚树。

考虑非树边 $e = (u, v)$ 不覆盖 $S$ 的充要条件：$S$ 全部在 $u$ 侧，$S$ 全部在 $v$ 侧，$u, v$ 侧均有属于 $S$ 的点。它将合法非树边的形态分成两类：

• 落在虚树上的点向虚树外延伸的某条边的对应子树内的返祖边。注意 “返祖边” 是在以该点为根时判定的。
• $u, v$ 对应树上路径被虚树的某条边完全包含。

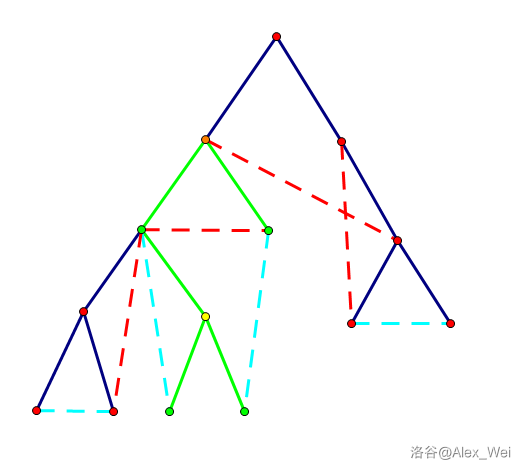
如上图，绿色的点表示 $S$，黄色的点不属于 $S$ 但属于虚树，橙色的点不属于虚树但落在虚树上。红色虚边为合法非树边，蓝色虚边为不合法非树边。

性质 B

对于性质 B，注意到不存在跨过 $d$ 的合法横叉边，因此可以将虚树改为我们通常所理解的虚树：若 $x$ 有两棵子树含属于 $S$ 的点，则 $x$ 也属于虚树。即认为 $d$ 属于虚树对答案无影响。

枚举 $S$ 的 LCA $d$，则不存在一端在 $d$ 子树内（不含 $d$），另一端在 $d$ 子树外的（不含 $d$）的合法非树边。因此子树内外独立，贡献直接相乘。

• 子树内的贡献可利用虚树结构 DP，因此设 $f_d$ 表示当 $d$ 属于虚树 时，仅考虑 $d$ 子树内所有关键点和非树边的贡献。
• 子树外的贡献为 $2 ^ {out_d}$，其中 $out_d$ 表示 $d$ 子树外以 $d$ 为根时的返祖边数量。设 $in_d$ 表示 $d$ 子树内以 $d$ 为根时的返祖边数量，换根 DP 求出 $in$ 和 $out$。$out$ 的求法稍有些复杂，留给读者自行思考，可以参考代码 dfs3 部分。

$f$ 的转移是重头戏。转移时，需要不重不漏地统计每一处贡献。为此，请读者牢记所有可能产生贡献的非树边形态：落在虚树上的点向虚树外延伸的某条边的对应子树内的返祖边；返祖边两端对应树上路径被虚树的某条边完全包含。

设 $d$ 的所有儿子为 $s_1\sim s_k$。$s_i$ 的子树内要么没有虚树上的点，要么有虚树上的点。对于后者，根据虚树的性质，有且仅有最浅的点与 $d$ 在虚树上相连。

设 $d$ 在虚树上的儿子为 $P$，有基本贡献系数 $\prod_{p\in P} f_p$。接下来统计未考虑到的非树边：

• 第一类非树边：对于每个 $p\in P$，包含于路径 $d\rightsquigarrow p$ 的非树边。
• 第二类非树边：对于每个 $p\in P$ 和所有 $q\in d\rightsquigarrow p$（不含 $d, p$），从 $q$ 向虚树外延伸的某条边的对应子树内的返祖边。
• 第三类非树边：对于 $d$，向虚树外延伸且在子树内的某条边的对应子树内的返祖边。

将第三类非树边摊到每个未选点的儿子，得：

• 对于选点的儿子 $s_i$，贡献系数为 $X(s_i) = \sum_{p\in \mathrm{subtree}(s_i)} g_{p\to d}$，其中 $g_{p\to d}$ 表示 $f_p$ 乘以 $2 ^ c$，其中 $c$ 表示包含于路径 $d\rightsquigarrow p$ 的非树边数量，加上对于所有 $q\in d\rightsquigarrow p$（不含 $d, p$），从 $q$ 向路径 $d\rightsquigarrow p$ 外延伸的某条边的对应子树的返祖边数量之和。
• 对于未选点的儿子 $s_i$，贡献系数为 $Y(s_i) = 2 ^ c$，其中 $c$ 表示 $s_i$ 子树内的返祖边数量 $in_{s_i}$，加上较浅的一端为 $d$，较深的一端落在 $s_i$ 子树内的返祖边数量。

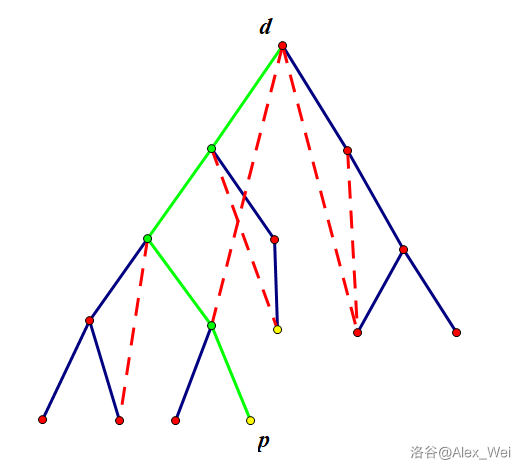
如上图，$d$ 的左子树选择点 $p$，红色虚边为产生贡献的非树边。$d$ 的右子树没有选择，红色虚边为产生贡献的非树边。

假设已经求出 $X(s_i)$ 和 $Y(s_i)$，考虑 $f_d$ 如何计算。设恰好在 $k$ 棵子树内选点的答案为 $F_k$，即 $F_k = [x ^ k]\prod (X(s_i) x + Y(s_i))$。

• 如果 $d\notin S$，则至少要有两棵子树被选择，产生贡献 $\sum_{k\geq 2} F_k$。
• 如果 $d\in S$，则要求 $d$ 是关键点，对被选择子树数量没有限制，产生贡献 $-\sum_{k\geq 0} F_k$。

发现 $k\geq 2$ 的 $F_k$ 等价，因此背包时维护 $F_0, F_1$ 和 $\sum_{k\geq 2} F_{k}$ 即可。

设 $Z = \sum_{1\leq i\leq n} f_i 2 ^ {out_i}$，则 $Z = \sum_{|S|\geq 1 \ \land \ S\subseteq U} (-1) ^ {|S|} 2 ^ {c(S)}$，答案为 $-Z$。

考虑维护 $g_{p\to d}$ 求 $X(s_i)$。根据 $g$ 的定义，可得如下步骤：

• 首先，对于 $p\in \mathrm{subtree}(d)$，令 $g_{p\to d}\gets g_{p\to s_i}$，其中 $s_i$ 是 $p$ 对应的 $d$ 的儿子。
• 对于所有 $s_i$，令 $g_{s_i\to d}\gets f_{s_i}$。由于不存在等于树边的非树边，将这一步放在下面两步之后也正确。
• 加入第一类非树边的贡献：枚举所有以 $d$ 为一端，另一端在 $d$ 子树内的非树边 $e = (d, u)$，对于 $p\in \mathrm{subtree}(u)$，将 $g_{p\to d}$ 乘以 $2$。
• 加入第二类非树边的贡献：枚举所有以 $s_i$ 为一端，另一端在 $s_i$ 子树内的非树边 $e = (s_i, u)$，设 $u$ 对应 $s_i$ 的儿子为 $v$，则对于 $s_i$ 的所有不为 $v$ 的儿子 $t_j\neq v$，对于 $p\in \mathrm{subtree}(t_j)$，将 $g_{p\to d}$ 乘以 $2$。简单地说，返祖边 $e = (u, v)$（其中 $u$ 是较浅端）会对 $u$ 的不为 $u\to v$ 后继的所有儿子的子树内所有结点产生贡献。

我使用的维护方法是：继承 $g$；加入第一类非树边的贡献；计算 $X$ 求出 $f$；加入以 $d$ 为较浅端的第二类非树边的贡献；令 $g_{d\to d} \gets f_d$。其实就是将统计第二类非树边的贡献下放到每个儿子处进行，这样好写一点，但注意这类贡献需要在计算 $X$ 求出 $f$ 之后统计。

将 $p$ 这一维用 DFS 序拍平到序列上，线段树合并维护 $g_{p\to d}$，支持区间乘法，区间求和。注意到每个子树的时间戳区间不交，所以不用线段树合并，只需用一棵线段树维护。

考虑求 $Y(s_i)$。在计算 $g_{p\to d}$，加入第一类非树边的贡献时，对于每个 $e = (d, u)$ 以及对应 $d$ 的儿子 $s_i$，将 $in_{s_i}$ 加上 $1$，过程结束后得到新的 $in'_{s_i}$。则 $Y(s_i) = 2 ^ {in'_{s_i}}$。

时间复杂度 $\mathcal{O}((n + m)\log n)$。

正解

相较于性质 B 多出了以 $1$ 为根时的横叉边。

考虑在何种情况下性质 B 的做法会导致错误：性质 B 保证我们可以将 $d$ 加入虚树，而性质 B 的做法在 “无论非树边是否是返祖边，只要 $d$ 在虚树上” 时，均可得到正确的答案，因为我们在分析合法非树边形态时，并没有要求这些非树边是以 $1$ 为根时的返祖边。这说明性质 B 只是 让我们将 $d$ 加入虚树。

将 $d$ 加入虚树会导致一些非树边从合法变成不合法。

• 对于形如 “落在虚树上的点向虚树外延伸的某条边的对应子树内的返祖边” 的非树边，由于将 $d$ 加入虚树不改变落在虚树的点集，因此不会有影响。
• 对于形如 “$u, v$ 对应树上路径被虚树的某条边完全包含” 的非树边，将 $d$ 加入虚树后产生的影响为：若虚树原本不包含 $d$，且存在经过 $d$ 的虚树边 $(x, y)$，那么一条两端均属于 $x, y$ 树上路径，且两端分别在 $d$ 的两侧的非树边从合法变成了不合法。

因此，只需重新计算这样的 $S$ 的贡献：$d\notin S$，且 $d$ 恰有 两棵子树有属于 $S$ 的点。

枚举 $d$ 和将 $d$ 加入虚树后它在虚树上的两个儿子 $p, q$，设它们分别对应 $d$ 在原树上的儿子 $u\neq v$。设 $z = g_{p\to d} \times g_{q\to d}\times \prod_{s_i \neq u, v} Y(s_i)$，这是原来计算的贡献。枚举 LCA 为 $d$ 的非树边 $e = (x, y)$，若 $x, y$ 分别在 $d\rightsquigarrow p$ 和 $d\rightsquigarrow q$ 上（路径不含 $d$，$x, y$ 顺序无关），则将 $z$ 乘以 $2$。最终得到 $z'$ 为真正的贡献。暴力做的复杂度是 $\mathcal{O}(n ^ 2 m)$。

先将 $s_i$ 子树时间戳区间的所有 $g$ 值乘以 $\frac 1 {Y(s_i)}$，最后将贡献乘以 $\prod_{s_i} Y(s_i)$（我们发现，实际上 $\prod_{s_i} Y(s_i) = 2 ^ {in_d}$），这样贡献只与 $g_{p\to d}$ 和 $g_{q\to d}$ 有关，而与其它儿子无关。

枚举 $d$，则一条 LCA 为 $d$ 的非树边的贡献是矩形乘以 $2$。若干次矩形乘以 $2$ 之后全平面求和，注意容斥掉 $u\neq v$ 的贡献。我使用的维护方法是：支持查找子树内某点 $x$ 对应的 $d$ 的儿子在时间戳上的后继 $\mathrm{suc}(x)$。扫描线，将所有儿子的时间戳加入事件，则遇到事件 $(x, l, r, c)$ 时（当前扫到时间戳 $x$，操作为给 $l\sim r$ 乘以 $c$），设上一次考虑的时间戳为 $x'$（初始值为 $d$ 的儿子时间戳最小值 $L = \mathrm{dfn}(d) + 1$）。因为所有儿子的时间戳也被加入了事件，所以 $x'\sim x - 1$ 一定是同一个儿子子树内的时间戳。求出 $x'\sim x - 1$ 的 $g$ 值之和，求出 $\mathrm{suc}(x')\sim R$ 的 $g$ 值之和（$R$ 表示 $d$ 的子树时间戳最大值 $\mathrm{dfn}(d) + \mathrm{size}(d) - 1$），相乘后再乘以 $2 ^ {out_d} \prod_{s_i} Y(s_i)$ 加入答案。

最后不要忘记将答案减去 $F_2 \times 2 ^ {out_d}$，也就是减去原先计算的错误答案。为此，需要区分 $F_2$ 和 $F_{k\geq 3}$，背包时维护 $F_0, F_1, F_2, \sum_{k\geq 3} F_{k}$。

时间复杂度 $\mathcal{O}((n + m)\log n)$，空间复杂度为 $\mathcal{O}(n + m)$，加上求 LCA 的空间复杂度。代码。