自动搬运

查看原文

来自洛谷，原作者为

	Rainbow_qwq **

搬运于2025-08-24 22:48:44，当前版本为作者最后更新于2023-07-29 17:24:05，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

我觉得这是 adhoc 好题啊，但是放在场上就区分上去了一些会猜 $k=0$ 结论的选手，区分度比较怪。

下面来复原一下考场想法。

称 $>n$ 编号的点为新点。

题目的限制很奇怪，首先思考一下原树对最终树形成了什么限制。

经过手玩得出的结论是：新点似乎只能插在原树的某条边上，或者塞在原树节点下面，那么原树是最终树的一棵虚树。

那新点形成若干个子树、若干条链，能不能设计一个子树合并的 dp 呢？试了试，貌似不太行。

那就从部分分一个一个考虑。先考虑 $n=1,k=0$。

子树合并不太行时因为限制了每一个 $\text{lca}$，想一想能否设计一个符合题目限制的状态？

我们的限制是 $\text{lca}(i,j)\le \max(i,j)+k$.

考虑把 $\max$ 去掉，一次一次地加点并满足：对于 $1\le j<i,\text{lca}(i,j)\le i+k$。

发现形式一下子变得比较好看，考虑一下 $k=0$ 的情况。

此时要求 $1\le j<i,\text{lca}(i,j)\le i$.

那么插入点 $i$ 时，只能插在某条边上，或者某个点下面开一个新点，方案数为 $2size-1$。接下来会递归成 $n\to n+1$ 的同等问题。

那么 $k=0$ 问题的答案就很显然了：

当然有的人暴力找规律就找出这一步了。

用同样的思想考虑 $k>0$。

考虑从小到大一个一个插入点。此时不一样的是，一个点 $i$ 和其他点的 $\text{lca}$ 可能在 $[i+1,i+k]$。

也就是可以在现在树上的一条边上衍生出一个叶子，新加两个点，一个点是 $i$，一个点在 $[i+1,i+k]$ 之间且未确定。

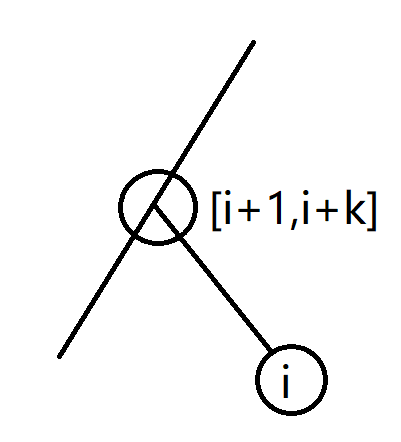
再形式化的描述一下，发现我们考虑的正是 $[1,i]$ 的虚树，而且虚树上的点必须在 $[1,i+k]$ 内！

也就是说，空白需要填的点只有 $[i+1,i+k]$ 这些可能，最多 $k$ 个。

那就可以进行状压 dp，设 $f(i,S)$ 表示插入了 $i$ 个点，并且前 $k$ 次加入的未被填掉的白点用一个状态 $S$ 表示。

转移有以下几种：

• 将 $i+1$ 插入在边上或挂在点下面，系数 $2size-1$。
• 将 $i+1$ 从一条边上衍生出来（加两个点），加入一个空白点，系数 $size-1$。
• 用 $i+1$ 填上一个空白点。

虚树节点 $size=i+\text{popcount}(S)$，那么就做完了。

时间复杂度 $O(Tmk2^k)$，代码用了 ull 加起来一起取模卡常。

#include<bits/stdc++.h>
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
#define ull unsigned long long

#define mod 1000000007
#define maxn 200005
#define inf 0x3f3f3f3f

int n,m,k,fa[maxn];
ull f[1<<10|5],g[1<<10|5];
int popc[1<<10|5];

void work()
{
	n=read(),m=read(),k=read();
	For(i,2,n)fa[i]=read();
	if(k==0){
		ull res=1;
		For(i,n,n+m-1)res=res*(i*2-1)%mod;
		cout<<res<<"\n";
		return;
	}
	memset(f,0,sizeof f),f[0]=1;
	int mxs=1<<k;
	For(i,n,n+m-1){
		For(s,(1<<(k-1)),(1<<k)-1)
			g[(s<<1)&(mxs-1)]+=f[s];
		For(s,0,(1<<(k-1))-1){
			Rep(j,k-2,0)
				if(s>>j&1) g[(s^(1<<j))<<1]+=f[s];
			g[s<<1]+=f[s]*((i+popc[s])*2-1);
			g[s<<1|1]+=f[s]*(i+popc[s]-1);
		}
		For(s,0,mxs-1) f[s]=g[s]%mod,g[s]=0;
	}
	cout<<f[0]<<"\n"; 
}

signed main()
{
	For(i,1,(1<<10)-1)popc[i]=popc[i>>1]+(i&1);
	read();int T=read();
	while(T--)work();
	return 0;
}