自动搬运

查看原文

来自洛谷，原作者为

	0x3F Wir müssen wissen, wir werden wissen.

搬运于2025-08-24 22:48:42，当前版本为作者最后更新于2023-06-28 10:28:11，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

假如没有地铁，那么每条边对答案的贡献为 $w\times S_1\times S_2$，其中 $S_1,S_2$ 为这条边把树分成的两部分分别的点权和，如图。

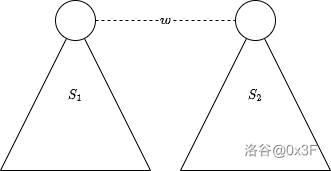
现在有了地铁，使得答案减少了 $D$。

假设一个人从 $A$ 到 $B$，其中 $a,p_1,p_2,\cdots,p_k,b$ 共 $k+2$ 个点，$k+1$ 条边与地铁重合（$k$ 可以为 $0$），那么对 $D$ 的贡献为：

$$(w_{a\to p_1}-w'_{a\to p_1})+(w_{p_1\to p_2}-w'_{p_1\to p_2})+\cdots+(w_{p_k\to b}-w'_{p_k\to b})-t $$

其中 $w_{u\to v}$ 表示从 $u$ 到 $v$ 的边的 $w$ 的值。

上式也可以改写为：

$$(w_{a\to p_1}-w'_{a\to p_1}-t)+t+(w_{p_1\to p_2}-w'_{p_1\to p_2}-t)+t+\cdots+t+(w_{p_k\to b}-w'_{p_k\to b}-t) $$

也就是说，在这个人移动的过程中，经过的地铁的每条边对 $D$ 产生的贡献为 $w-w'-t$，每个“内点”（不是 $a,b$ 的点）对 $D$ 产生的贡献为 $t$，如图。

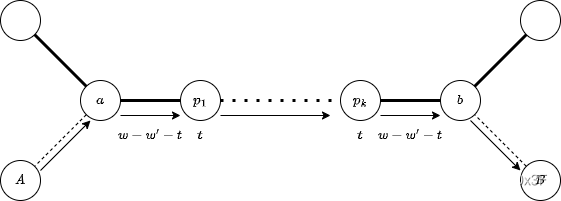
考虑每条边和每个点产生贡献的次数。

每条边产生贡献，当且仅当它被经过。因此次数等于 $S_1S_2$，其中 $S_1,S_2$ 为这条边把树分成的两部分分别的点权和。

每个点产生贡献，当且仅当它作为“内点”被经过。由于地铁是一条链，在链上，与之相邻的两条边均被经过。因此次数等与 $S_1S_3$，其中 $S_1,S_3$ 为这两条边把树分成的三部分中，不包含该点的两部分分别的点权和。端点的贡献为 $0$。

因此对 $D$ 的贡献分别为 $S_1S_2(w-w'-t)$ 和 $S_1S_3t$，如图。

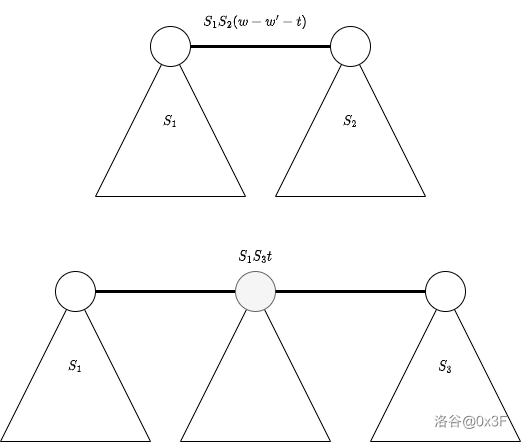
可以使用树形 DP 求出 $D$ 的最大值。

如果树根为 $1$，记 $dp_{i}(i\ne1)$ 表示如果链的一端为 $i$ 的父亲，另一端在 $i$ 的子树内，那么这条链产生的贡献，最大是多少。

转移有两种可能性：

一、另一端就是 $i$。此时只有 $i$ 连向父亲的边产生贡献。

即 $dp_{i}\gets(w_{i\to f_{i}}-w'_{i\to f_{i}}-t)siz_{i}(N-siz_{i})$。

其中 $f_{u}$ 表示 $u$ 的父亲，$siz_{u}$ 表示 $u$ 的子树内点权之和，$N$ 表示所有点权之和。

二、另一端不是 $i$。假设另一端在 $j$ 的子树内，则不仅 $i$ 连向父亲的边产生贡献，而且 $i$ 从端点变为内点，产生贡献。

即 $dp_{i}\gets(w_{i\to f_{i}}-w'_{i\to f_{i}}-t)siz_{i}(N-siz_{i})+tsiz_{j}(N-siz_i)+dp_j$。

如图。

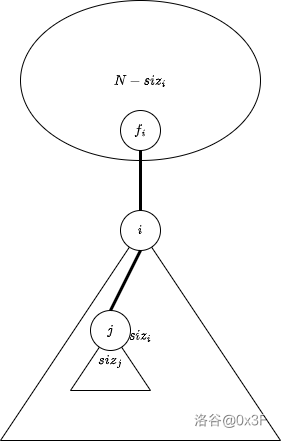
假设 $r$ 是地铁中深度最浅的点。

如果 $r$ 是端点，与 $r$ 相邻的是 $s$（是 $r$ 的儿子），那么 $D\gets dp_s$。

如果 $r$ 不是端点，与 $r$ 相邻的是 $s,t$（都是 $r$ 的儿子），由于点 $r$ 是内点，产生贡献，那么 $D\gets dp_s+dp_t+tsiz_ssiz_t$。

如图。

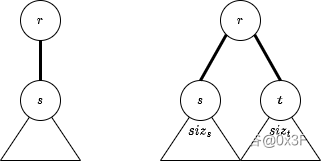
如果暴力枚举 $s,t$，会超时，应当使用斜率优化。

如果有 $siz$ 相同的，那么选取 $dp$ 最大和次大的作为 $s,t$，计入答案。

然后将 $siz$ 去重，只保留 $dp$ 最大的，将 $siz$ 从小到大排序。

由 $D=dp_s+dp_t+tsiz_ssiz_t$，移项得：

$$\underset{y}{\underline{dp_s}}=\underset{k}{\underline{-tsiz_t}}\times\underset{x}{\underline{siz_s}}+\underset{b}{\underline{D-dp_t}} $$

由于 $k,x$ 均单调，可以使用单调队列维护凸包。

时间复杂度为 $O(n\log n)$。

代码：

#include <bits/stdc++.h>
using namespace std;
const int _ = 1e5 + 10;
const int __ = 2e5 + 10;
int id, n, t, e, hd[_], nx[__], to[__], ln1[__], ln2[__];
long long siz[_], N;
__int128 dp[_];
inline void add(int u, int v, int w1, int w2) {
	e++;
	nx[e] = hd[u];
	to[e] = v;
	ln1[e] = w1;
	ln2[e] = w2;
	hd[u] = e;
}
__int128 sum, dif;
void dfs1(int x, int f) {
	for (int i = hd[x]; i; i = nx[i]) {
		int y = to[i];
		if (y != f) {
			dfs1(y, x);
			siz[x] += siz[y];
			sum += __int128(siz[y]) * (N - siz[y]) * (ln1[i]);
		}
	}
}
int m;
struct node {
	__int128 x;
	__int128 y;
} arr[_];
int l, r, q[_];
inline bool cmp(node a, node b) {
	if (a.x == b.x) return (a.y > b.y);
	return (a.x < b.x);
}
inline bool eqn(node a, node b) {
	return (a.x == b.x);
}
inline __float128 slope(node a, node b) {
	return ((__float128)(b.y - a.y) / (__float128)(b.x - a.x));
}
void dfs2(int x, int f, __int128 z) {
	dp[x] = z;
	for (int i = hd[x]; i; i = nx[i]) {
		int y = to[i];
		if (y != f) {
			dfs2(y, x, __int128(siz[y]) * (N - siz[y]) * (ln1[i] - ln2[i] - t));
			if (f) dp[x] = max(dp[x], dp[y] + z + __int128(siz[y]) * (N - siz[x]) * (t));
			dif = max(dif, dp[y]);
		}
	}
	m = 0;
	for (int i = hd[x]; i; i = nx[i]) {
		int y = to[i];
		if (y != f) {
			m++;
			arr[m].x = siz[y];
			arr[m].y = dp[y];
		}
	}
	sort(arr+1, arr+m+1, cmp);
	for (int i = 1; i < m; i++) {
		if (arr[i].x == arr[i+1].x) {
			dif = max(dif, arr[i].y + arr[i+1].y + t * arr[i].x * arr[i+1].x);
		}
	}
	m = unique(arr+1, arr+m+1, eqn) - arr - 1;
	l = r = 1;
	q[1] = 1;
	for (int i = 2; i <= m; i++) {
		while (r > l && slope(arr[q[l]], arr[q[l+1]]) > (-t * arr[i].x)) l++;
		dif = max(dif, arr[i].y + arr[q[l]].y + t * arr[i].x * arr[q[l]].x);
		while (r > l && slope(arr[q[r]], arr[i]) > slope(arr[q[r-1]], arr[i])) r--;
		q[++r] = i;
	}
}
int main() {
	cin >> id >> n >> t;
	for (int i = 1; i <= n; i++) {
		cin >> siz[i];
		N += siz[i];
	}
	for (int i = 1; i < n; i++) {
		int u, v, w1, w2;
		cin >> u >> v >> w1 >> w2;
		add(u, v, w1, w2);
		add(v, u, w1, w2);
	}
	dfs1(1, 0);
	dfs2(1, 0, __int128(0));
	__int128 ans = sum - dif;
	string str;
	while (ans) {
		str = (char)((ans % 10) + 48) + str;
		ans /= 10;
	}
	cout << str << endl;
	return 0;
}