自动搬运

查看原文

来自洛谷，原作者为

	0x3F Wir müssen wissen, wir werden wissen.

搬运于2025-08-24 22:48:42，当前版本为作者最后更新于2023-06-28 10:26:08，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

由期望的线性性可知，总分的期望等于每一道题得分的期望之和。

我们可以把题分为 $5$ 类：

1. 题号对应，个数为 $C_ {eq}$。
2. 题号不对应，应该填单选题，实际填单选题，个数为 $C_{11}$。
3. 题号不对应，应该填单选题，实际填多选题，个数为 $C_{12}$。
4. 题号不对应，应该填多选题，实际填单选题，个数为 $C_{21}$。
5. 题号不对应，应该填多选题，实际填多选题，个数为 $C_{22}$。

同时，这 $5$ 类题单个对答案的贡献分别为 $S_{eq},S_{11},S_{12},S_{21},S_{22}$。

答案为：$C_{eq}S_{eq}+C_{11}S_{11}+C_{12}S_{12}+C_{21}S_{21}+C_{22}S_{22}$。

首先，求 $C_{eq},C_{11},C_{12},C_{21},C_{22}$ 的值。

假设第 $i$ 行第 $j$ 列的题的坐标为 $(i,j)$，那么横向排列时其题号为 $(i-1)m+j$，纵向排列时其题号为 $(j-1)n+i$。

如果不考虑题号是否对应，那么应该填单选题，实际填单选题的个数 $C_{11}'$ 就是满足 $(i-1)m+j\le k,(j-1)n+i\le k$ 的 $(i,j)$ 的数量。

满足 $(i-1)m+j\le k$ 的区域可以分拆为两个矩形 $R_1=[1,\lfloor\frac{k}{m}\rfloor]\times[1,m]$ 和 $R_2=[\lfloor\frac{k}{m}\rfloor+1,\lfloor\frac{k}{m}\rfloor+1] \times [1,k\bmod m]$ 的不交并，如图所示。

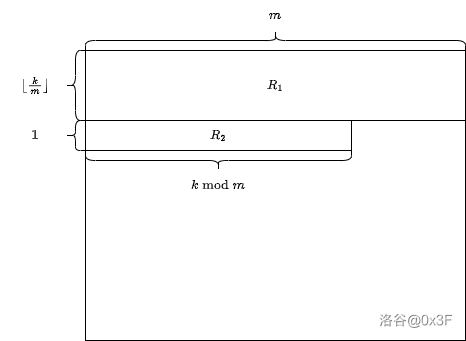
满足 $(j-1)n+i\le k$ 的区域也可以分拆成两个矩形 $R_3,R_4$。

可以求出 $C_{11}'=\vert(R_1 \cup R_2) \cap (R_3 \cup R_4)\vert = \vert R_1\cap R_3\vert + \vert R_1\cap R_4\vert + \vert R_2\cap R_3\vert + \vert R_2\cap R_4\vert$。

而矩形的交的计算是非常简单的。

同时，显然有 $C_{12}=k-C_{11}',C_{21}=k-C_{11}',C_{22}'=nm-C_{11}'-C_{12}-C_{21}$。

接下来考虑题号对应的情况。题号对应时，有 $(i-1)m+j=(j-1)n+i$，即 $(i-1)(m-1)=(j-1)(n-1)$。

记 $\gcd(n-1,m-1)=g$，则 $\gcd(\frac{n-1}{g},\frac{m-1}{g})=1$， 故 $(i-1)\times\frac{m-1}{g}=(j-1)\times\frac{n-1}{g}$，当且仅当 $i-1=\frac{t(n-1)}{g},j-1=\frac{t(m-1)}{g}$，其中 $t\in\mathbb{Z}$ 且 $0\le t\le g$。

此时，题号为 $(i-1)m+j=(j-1)n+i=\frac{t(nm-1)}{g}+1$。

当题号对应的这题为单选题时，有 $\frac{t(nm-1)}{g}+1\le k$，即 $t\le\lfloor\frac{(k-1)g}{nm-1}\rfloor$，因此 $C_{11}=C_{11}'-(\lfloor\frac{(k-1)g}{nm-1}\rfloor+1)$。同理，$C_{22}=C_{22}'-(\lfloor\frac{(nm-k-1)g}{nm-1}\rfloor+1)$。由于 $t$ 的取值共有 $g+1$ 种，故 $C_{eq}=g+1$。

注意特判 $n=m=1$。

接下来，求 $S_{eq},S_{11},S_{12},S_{21},S_{22}$ 的值。

$S_{eq}$：显然为 $1$。

$S_{11}$：显然为 $\frac{1}{c}$。

$S_{12}$：显然为 $0$。

$S_{21}$：为 $\frac{1}{c}$。假设多选题有 $a$ 个选项，则有 $\frac{a}{c}$ 的概率得 $\frac{1}{a}$ 分，无论多选题的选项是怎样的，得分期望都为 $\frac{1}{c}$。

$S_{22}$：一道多选题的选项共有 $2^c-c-2$ 种可能，因此符合条件的选项 $(A,B)$ 共有 $(2^c-c-2)^2$ 种。考虑计算这些 $(A,B)$ 的得分之和。

假设 $\vert A\vert=i,\vert B\vert=j$，$A$ 有 $\mathrm{C}_{c}^{i}$ 种选法，由于 $B\sube A$，故 $B$ 有 $\mathrm{C}_{i}^{j}$ 种选法，对答案的贡献为 $\frac{j}{i}$。同时，有 $2\le i\le c-1,2\le j\le i$ 的限制。因此，得分之和为：

$$\sum_{i=2}^{c-1}\sum_{j=2}^{i}\mathrm{C}_{c}^{i}\mathrm{C}_{i}^{j}\frac{j}{i} $$$$=\sum_{i=2}^{c-1}\frac{\mathrm{C}_{c}^{i}}{i}\sum_{j=2}^{i}j\mathrm{C}_{i}^{j} $$

由二项式定理，$(x+y)^{n}=\mathrm{C}_{n}^{0}y^{n}+\mathrm{C}_{n}^{1}xy^{n-1}+\cdots+\mathrm{C}_{n}^{n}x^n$，令 $y\gets1$，得：

$$(x+1)^{n}=\mathrm{C}_{n}^{0}+\mathrm{C}_{n}^{1}x+\mathrm{C}_{n}^{2}x^2+\mathrm{C}_{n}^{3}x^3+\cdots+\mathrm{C}_{n}^{n}x^n(\star) $$

$(\star)$ 两边关于 $x$ 求导，得：

$$n(x+1)^{n-1}=\mathrm{C}_{n}^{1}+2\mathrm{C}_{n}^{2}x+3\mathrm{C}_{n}^{3}x^2+\cdots+n\mathrm{C}_{n}^{n}x^{n-1} $$

令 $x\gets 1,n\gets i$ 得：

$$i2^{i-1}=\mathrm{C}_{i}^{1}+2\mathrm{C}_{i}^{2}+3\mathrm{C}_{i}^{3}+\cdots+i\mathrm{C}_{i}^{i} $$

移项得：

$$2\mathrm{C}_{i}^{2}+3\mathrm{C}_{i}^{3}+\cdots+i\mathrm{C}_{i}^{i}=i2^{i-1}-\mathrm{C}_{i}^{1}=i(2^{i-1}-1) $$

故原式可化简为：

$$\sum_{i=2}^{c-1}\frac{\mathrm{C}_{c}^{i}}{i}\times i(2^{i-1}-1) $$$$=\frac{1}{2}\sum_{i=2}^{c-1}2^{i}\mathrm{C}_{c}^{i}-\sum_{i=2}^{c-1}\mathrm{C}_{c}^{i} $$

$(\star)$ 中，令 $x\gets 1,n\gets c$ 得：

$$2^c=\mathrm{C}_{c}^{0}+\mathrm{C}_{c}^{1}+\mathrm{C}_{c}^{2}+\mathrm{C}_{c}^{3}+\cdots+\mathrm{C}_{c}^{c-1}+\mathrm{C}_{c}^{c} $$

移项得：

$$\mathrm{C}_{c}^{2}+\mathrm{C}_{c}^{3}+\cdots+\mathrm{C}_{c}^{c-1}=2^c-\mathrm{C}_{c}^{0}-\mathrm{C}_{c}^{1}-\mathrm{C}_{c}^{c}=2^c-c-2 $$

$(\star)$ 中，令 $x\gets 2,n\gets c$ 得：

$$3^c=\mathrm{C}_{c}^{0}+2\mathrm{C}_{c}^{1}+4\mathrm{C}_{c}^{2}+8\mathrm{C}_{c}^{3}+\cdots+2^{c-1}\mathrm{C}_{c}^{c-1}+2^{c}\mathrm{C}_{c}^{c} $$

移项得：

$$4\mathrm{C}_{c}^{2}+8\mathrm{C}_{c}^{3}+\cdots+2^{c-1}\mathrm{C}_{c}^{c-1}=3^c-\mathrm{C}_{c}^{0}-2\mathrm{C}_{c}^{1}-2^{c}\mathrm{C}_{c}^{c}=3^c-2^c-2c-1 $$

故原式可化简为：

$$\frac{3^c-2^c-2c-1}{2}-(2^c-c-2)$$ $$=\frac{3^c-3\times2^c+3}{2}$$

故 $S_{22}=\frac{3^c-3\times2^c+3}{2(2^c-c-2)^2}$。

时间复杂度为 $O(\log n+\log m+\log c)$。

代码：

#include <bits/stdc++.h>
using namespace std;
const int p = 1e9 + 7;
inline int qpow(int a, long long b) {
	int s = 1;
	while (b) {
		if ((b & 1LL)) s = (long long)s * a % p;
		a = (long long)a * a % p;
		(b >>= 1LL);
	}
	return s;
}
int n, m, c;
long long nm, k;
long long ceq, c11, c12, c21, c22;
int seq, s11, s12, s21, s22;
int ans;
int main() {
	cin >> n >> m >> k >> c;
	nm = (long long)n * m;
	c11 = (k/m) * (k/n) + min(k/n, k%m) + min(k%n, k/m) + (k/m < k%n && k/n <= k%m);
	c12 = k - c11;
	c21 = k - c11;
	c22 = nm - c11 - c12 - c21;
	int g = __gcd(n-1, m-1);
    long long step = ((g) ? ((nm - 1) / g) : (1LL));
	ceq = g+1;
	c11 -= (step + k - 1) / step;
	c22 -= (step + nm - k - 1) / step;
	seq = 1;
	s11 = qpow(c, p-2);
	s12 = 0;
	s21 = qpow(c, p-2);
	s22 = ((((long long)qpow(3, c) - 3LL * qpow(2, c) + 3) % p + p) % p * qpow(2, p-2) % p) * qpow(((qpow(2, c) - c - 2) % p + p) % p, p-3) % p;
	ans = (ans + ceq % p * seq) % p;
	ans = (ans + c11 % p * s11) % p;
	ans = (ans + c12 % p * s12) % p;
	ans = (ans + c21 % p * s21) % p;
	ans = (ans + c22 % p * s22) % p;
	cout << ans << endl;
	return 0;
}