1 条题解
-
0
自动搬运
来自洛谷,原作者为

EdenSky
壶关见主页 || NOIP RP ++ || 主页 https://www.luogu.com/article/w68nh64h搬运于
2025-08-24 22:48:31,当前版本为作者最后更新于2023-07-16 22:38:37,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
P9455 塔台超频(hard)
写在前面:本题蒟蒻给出两种做法,一种乱搞贪心(只是目前能过,若能被 Hack 请和我说),一种正解二分。
正文 1
最坏时间复杂度:
这个做法是很简单的,在此不多讲。只需要二分超频电压
mid即可,若当前mid可行,则令右边界缩小至mid,否则令左边界扩大至mid。接下来是重要的
check()函数的编写,请注意塔台之间传输的路线不限,比如塔台 1 可以直接和塔台 通讯。也就是说对于每个塔台 ,我们首先要确认它向右的通讯范围是目前最大的。代码:
#include<iostream> using namespace std; const int N=5e5+7; int n,a[N],b[N]; bool check(int x){//判定当前超频电压x的值是否可行 int t=a[1]+b[1]+x;//起始位 for(int i=2;i<=n;i++) if(t>=a[i])//若该塔台可以覆盖下一个塔台 t=max(t,a[i]+b[i]+x);//求出更远的可以覆盖到的距离 else return 0;//否则不可行 return 1; } int main(){ ios::sync_with_stdio(false),cin.tie(0); cin>>n; for(int i=1;i<=n;i++) cin>>a[i]>>b[i]; long long l=0,r=1e9+1,mid; while(l<r){//二分 mid=(l+r)>>1; if(check(mid)) r=mid; else l=mid+1; } cout<<l; }正文 2
最坏时间复杂度:
设答案为 。
我们简化一下正文 1 的思路,当塔台 的范围被前一个炮台 的范围覆盖,即 ,我们可以忽略塔台 的范围,直接用塔台 的参数贪心即可。
if(a[i]+b[i]+ans>=a[i+1]+b[i+1]+ans) {a[i+1]=a[i],b[i+1]=b[i]; continue;}接下来是贪心,对于每个塔台 ,只需考虑它能否覆盖到 即可,若 无法覆盖 ,则增加超频至可以覆盖到。即:若 ,。
if(a[i]+b[i]+ans>=a[i+1]) continue; ans=max(ans,a[i+1]-a[i]-b[i]);当然,贪心要有正确性证明。本贪心的思路就是若塔台 能到达的最右范围比 远,则忽略 ,且对于每个 ,若 无法通讯 ,则增加超频(本段纯属废话)。
证明:
设超频 。
若 范围大于 ,则 到 所需要增加的 一定不多于 到 ,因此对于所有 ,若其范围被 覆盖,则将其扔掉(忽略)。
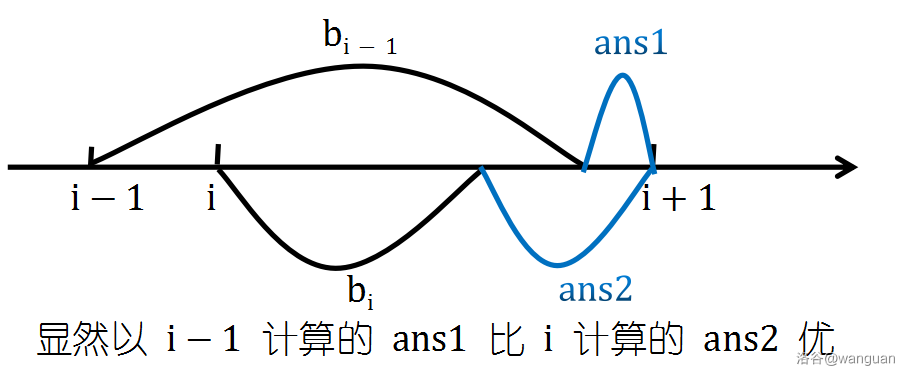
对于每个 , 到 的距离比 到 更远,因此 到 所需 比到 少。 到 有两种方式,即传输路线是否有 。
因为存在前提: 所能到达的最右距离比 远(不然 会被扔掉),所以在相同的 情况下,经过 能到更远,距离 更近,所需增加的 更少。于是对于所有 ,只需计算 到 所需的 即可,因为这样最优。
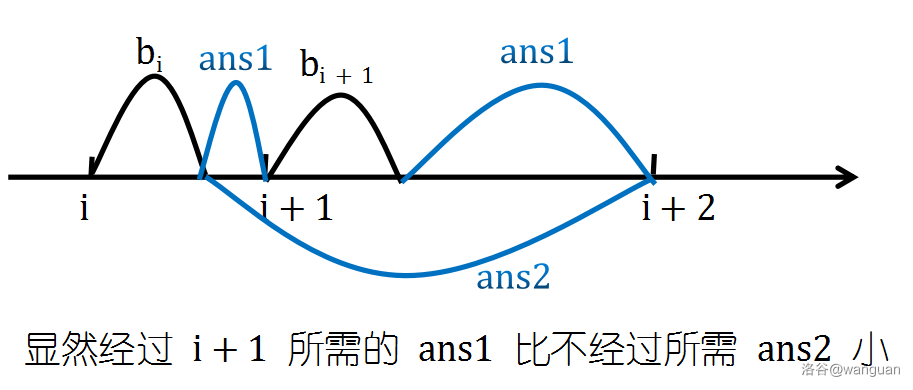
综合一下一个乱搞的贪心就出来了。
代码:
#include<iostream> using namespace std; const int N=5e5+7; int n,ans,a[N],b[N]; int main(){ ios::sync_with_stdio(false),cin.tie(0); cin>>n; for(int i=1;i<=n;i++) cin>>a[i]>>b[i]; for(int i=1;i<n;i++){ if(a[i]+b[i]+ans>=a[i+1]+b[i+1]+ans) {a[i+1]=a[i],b[i+1]=b[i]; continue;} if(a[i]+b[i]+ans>=a[i+1]) continue; ans=a[i+1]-a[i]-b[i]; } cout<<ans; }贪心 AC 记录,可以看到贪心快了 0.17 秒。
- 1
信息
- ID
- 8912
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 2
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
