自动搬运

查看原文

来自洛谷，原作者为

	Diaоsi Enemy of God

搬运于2025-08-24 22:48:24，当前版本为作者最后更新于2025-03-03 13:33:39，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

[ICPC 2021 WF] Guardians of the Gallery

如果把问题变成让保安走到雕塑所在的位置该怎么做？类似于 Airport Construction 的分析，保安只会走多边形顶点之间的线段（起点终点也当作顶点）。枚举两端点判断线段是否在多边形内，然后建图跑最短路。

回到原问题，发现能够看到雕塑的位置是多边形内的一个区域。而这个区域的边界形如雕塑位置和多边形上端点的连线（被一个“角”所遮挡视线）。

枚举这些射线，找到在多边形内的极长线段（即最长的合法可视边界）。求出每个顶点到这条线段的最短路线，判断这条路线是否在多边形内并更新该顶点到雕塑的最短距离。

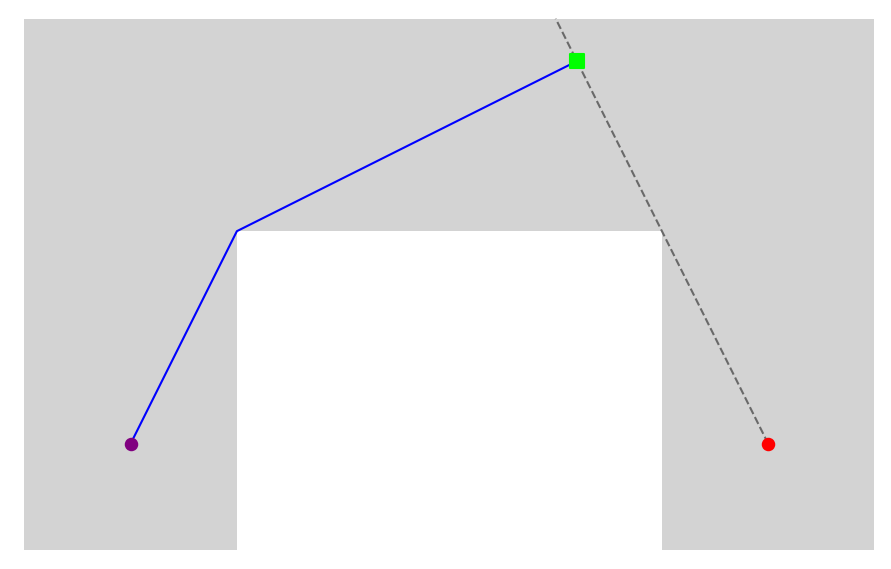
但是真的有这么简单吗？仔细思考一下，发现存在许多 corner case。首先，可视边界与多边形的边的交点可能作为终点：

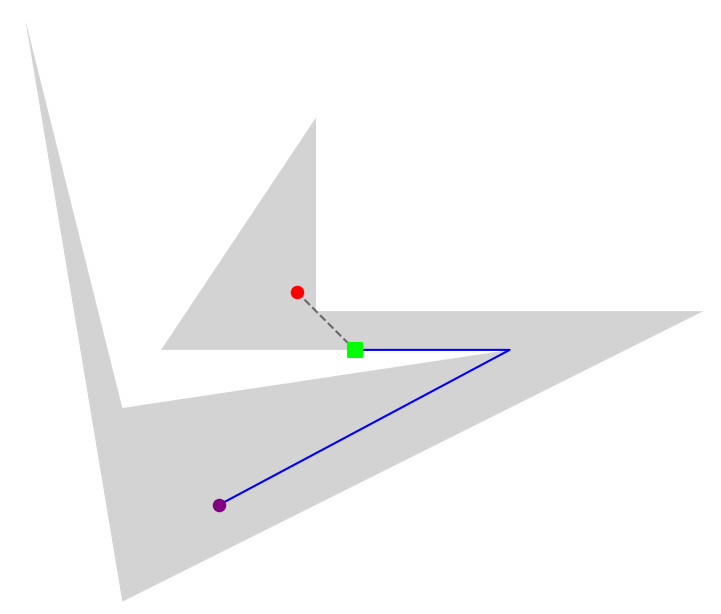
其次，可视区域要求能够至少看到雕塑的一半，因此这条射线不能被“双边遮挡”：

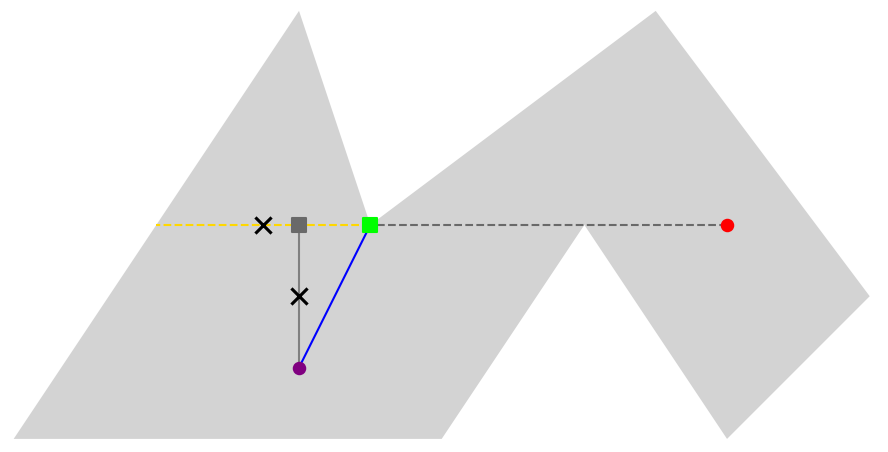
如上图，走到黄色虚线处是无法看到雕塑的，最短路径是走到绿色方点处。判断是否“双边遮挡”的方法有很多，可以开计数器分别记录射线左右两边分别有多少个端点与线段相切。保安的路线不需要判断“双边遮挡”。

分析一下我们干了啥：枚举雕塑沿着顶点方向射线、求出这条射线与多边形的所有交点、更新每个顶点到这个点最短距离（需要判断合法）。直接实现的复杂度是 $\mathcal{O}(n^4)$ 的，精细实现可以做到 $\mathcal{O}(n^3)$。

判断遮挡的部分参考了

#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pb push_back
typedef long long ll;
typedef double ld;
using namespace std;
const int N=210,M=20010,INF=0x3f3f3f3f;

const ld eps=1e-9,pi=acos(-1),inf=1e18;

mt19937_64 rnd(chrono::steady_clock::now().time_since_epoch().count());

int dcmp(ld x){return x<-eps?-1:(x>eps?1:0);}

struct node{
	ld x,y;
	node(ld xx=0,ld yy=0){x=xx,y=yy;}
	void in(){cin>>x>>y;}
	void out(){cout<<'('<<x<<','<<y<<')'<<'\n';}
	bool operator <(const node &a)const{
		return dcmp(x-a.x)?x<a.x:y<a.y;//x!=a.x
	}
	bool operator >(const node &a)const{
		return dcmp(x-a.x)?x>a.x:y>a.y;//x!=a.x
	}
	bool operator ==(const node &a)const{
		return !dcmp(x-a.x)&&!dcmp(y-a.y);//x==a.x&&y==a.y
	}
	bool operator !=(const node &a)const{
		return dcmp(x-a.x)||dcmp(y-a.y);//x!=a.x||y!=a.y
	}
};

node operator +(const node &a,const node &b){return node(a.x+b.x,a.y+b.y);}
node operator -(const node &a,const node &b){return node(a.x-b.x,a.y-b.y);}
node operator *(const ld &x,const node &a){return node(x*a.x,x*a.y);}
node operator /(const node &a,const ld &x){return node(a.x/x,a.y/x);}
ld operator *(const node &a,const node &b){return a.x*b.x+a.y*b.y;}
ld operator ^(const node &a,const node &b){return a.x*b.y-a.y*b.x;}

ld sqr(ld x){return x*x;}
ld len(node a){return sqrt(a*a);}
ld dist(node a,node b){return len(a-b);}

node normal(node a){return node(-a.y,a.x);}

node proj(node a,node b,node p){
	node d=b-a;
	return a+((d*(p-a))/(d*d))*d;
}

bool contain(node a,node b,node c){
	node x=a-b,y=c-b;
	return (!dcmp(x^y))&&(dcmp(x*y)<=0);
}

node intersect(node a,node b,node c,node d){
	//intersection of two lines
	node x=b-a,y=d-c,z=a-c;
    return a+((y^z)/(x^y))*x;
}

bool check(node a,node b,node c,node d){
    if(max(a.x,b.x)<min(c.x,d.x)||max(a.y,b.y)<min(c.y,d.y)||
        max(c.x,d.x)<min(a.x,b.x)||max(c.y,d.y)<min(a.y,b.y))return 0;
    return 1;
}

int inter(node a,node b,node c,node d){
    if(!check(a,b,c,d))return 0;
    node cd=d-c,ca=a-c,cb=b-c;
    ll x=dcmp(cd^ca),y=dcmp(cd^cb);
    if(x>0&&y>0)return 0;
    if(x<0&&y<0)return 0;
    if(x==0||y==0)return 1;
    node ab=b-a,ac=c-a,ad=d-a;
    x=dcmp(ab^ac),y=dcmp(ab^ad);
    if(x>0&&y>0)return 0;
    if(x<0&&y<0)return 0;
    if(x==0||y==0)return 1;
    return 2;
}

int n;
ld g[N][N];

node p[N],s,e;
vector<node> v;

int pre(int i){return i==1?n:i-1;}
int nxt(int i){return i==n?1:i+1;}

bool lineonseg(node a,node b,node c,node d){
	return dcmp((b-a)^(c-a))*dcmp((b-a)^(d-a))<=0;
}

bool parallel(node a,node b,node c,node d){
	return !dcmp((b-a)^(d-c));
}

bool inangle(node a,node b,node c){
	if(dcmp(a^b)>0)return dcmp(a^c)>=0&&dcmp(c^b)>=0;
	return !(dcmp(b^c)>0&&dcmp(c^a)>0);
}

int cnt[3];

bool seginpoly(node a,node b,int op){
	if(a==b)return 1;
	cnt[0]=cnt[1]=cnt[2]=0;
	for(int i=1;i<=n;i++){
		node u=p[i],v=p[nxt(i)],w=p[pre(i)];
		if(inter(a,b,u,v)==2)return 0;
		if(contain(a,u,b)){
			if(a!=u&&!inangle(a-u,v-u,w-u))return 0;
			if(b!=u&&!inangle(b-u,v-u,w-u))return 0;
			if(op&&a!=u&&b!=u){
				cnt[dcmp((v-u)^(b-a))+1]++;
				cnt[dcmp((w-u)^(b-a))+1]++;
				if(cnt[0]&&cnt[2])return 0;
			}
		}
		else{
			if(a!=u&&a!=v&&contain(u,a,v)&&dcmp((b-a)^(v-u))>0)return 0;
			if(b!=u&&b!=v&&contain(u,b,v)&&dcmp((b-a)^(v-u))<0)return 0;
		}
	}
	return 1;
}

void ext(int w){
	node a=p[w];
	for(int i=1;i<=n+2;i++){
		if(i==w)continue;
		node c=p[i],d=proj(e,a,c);
		if(seginpoly(c,d,0)&&seginpoly(d,e,1)){
			g[i][n+2]=min(g[i][n+2],dist(c,d));
			g[n+2][i]=min(g[n+2][i],dist(c,d));
		}
	}
	for(int i=1;i<=n;i++){
		node u=p[i],v=p[nxt(i)];
		if(parallel(a,e,u,v))continue;
		node t=intersect(a,e,u,v);
		if(!seginpoly(e,t,1))continue;
		for(int j=1;j<=n+2;j++){
			if(!seginpoly(p[j],t,0))continue;
			g[j][n+2]=min(g[j][n+2],dist(p[j],t));
			g[n+2][j]=min(g[n+2][j],dist(p[j],t));
		}
	}
}

int main(){
	ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++)p[i].in();
	s.in();p[n+1]=s;
	e.in();p[n+2]=e;
	if(seginpoly(s,e,1)){
		cout<<"0.000000000000000\n";
		return 0;
	}
	for(int i=1;i<=n+2;i++)
		for(int j=1;j<=n+2;j++)
			if(i^j)g[i][j]=seginpoly(p[i],p[j],0)?dist(p[i],p[j]):inf;
	for(int i=1;i<=n+1;i++)ext(i);
	for(int k=1;k<=n+2;k++)
		for(int i=1;i<=n+2;i++)
			for(int j=1;j<=n+2;j++)
				g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
	cout<<fixed<<setprecision(15)<<g[n+1][n+2]<<'\n';
	return 0;
}