自动搬运

查看原文

来自洛谷，原作者为

	iyaang 不因过往而自卑

搬运于2025-08-24 22:48:24，当前版本为作者最后更新于2023-07-19 19:59:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

赛博的阅读体验

题目链接

判无解是容易的，即为陷阱在起点到钥匙的路径上。

记所有边长和为 $A$，先考虑没有钥匙和陷阱怎么做，以起点为根，其他边都需要遍历两边，因为要回来去遍历其他边；只有一段叶子到最低分叉点的路径可以不走，那我们肯定贪心的选取最长的那一段，记其为 $L$，答案即为 $2A - L$。

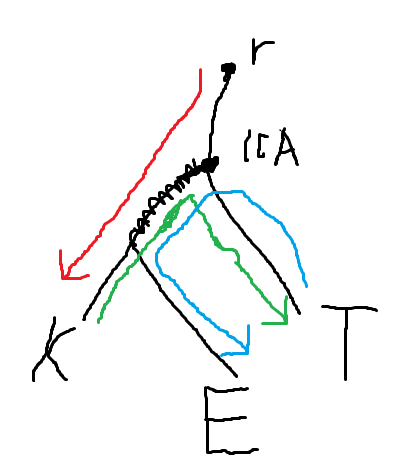
记 $K$ 为钥匙节点，$T$ 为陷阱节点，$E$ 为上面选出的最长的一段，则红 $\to$ 绿 $\to$ 蓝的走法是最优的，能够发现黑色锯齿线我们需要经过三次。

没有修改操作，直接离线询问挂在节点上。对于每个有询问的节点 dfs 一次，求出其到每个节点的距离以及 dfs 序用以判断祖先关系。接下来求出每个节点在 dfs 序上前后的最大距离，即到达该节点的最长距离和从此房间出发所需的最长距离，这样方便我们求出最远的只走一次的那段路径。接下来遍历钥匙节点到钥匙和陷阱的 LCA 间的每一个点来找到只走一段的距离，具体实现可以让钥匙节点一直跳父亲并对当前节点的 $pre$ 和 $suf$ 值取 $\max$，直到钥匙节点跳成陷阱节点的祖先。如果还是不懂柿子可以直接看代码和图进行理解。

时间复杂度 $\mathcal O(qn)$，官方题解说应该能倍增等一系列方法优化到 $\mathcal O(q \log n)$，不过我这样直接就过了，而且跑的还挺快，可能数据确实水。

#include<bits/stdc++.h>
#define ld long double
#define ui unsigned int
#define ull unsigned long long
#define int long long
#define eb emplace_back
#define pb pop_back
#define ins insert
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define power(x) ((x)*(x))
#define gcd(x,y) (__gcd((x),(y)))
#define lcm(x,y) ((x)*(y)/gcd((x),(y)))
#define lg(x,y)  (__lg((x),(y)))
using namespace std;

namespace FastIO
{
    template<typename T=int> inline T read()
    {
        T s=0,w=1; char c=getchar();
        while(!isdigit(c)) {if(c=='-') w=-1; c=getchar();}
        while(isdigit(c)) s=(s*10)+(c^48),c=getchar();
        return s*w;
    }
    template<typename T> inline void read(T &s)
    {
        s=0; int w=1; char c=getchar();
        while(!isdigit(c)) {if(c=='-') w=-1; c=getchar();}
        while(isdigit(c)) s=(s*10)+(c^48),c=getchar();
        s=s*w;
    }
    template<typename T,typename... Args> inline void read(T &x,Args &...args)
    {
        read(x),read(args...);
    }
    template<typename T> inline void write(T x,char ch)
    {
        if(x<0) x=-x,putchar('-');
        static char stk[25]; int top=0;
        do {stk[top++]=x%10+'0',x/=10;} while(x);
        while(top) putchar(stk[--top]);
        putchar(ch);
        return;
    }
}
using namespace FastIO;

namespace MTool
{   
    #define TA template<typename T,typename... Args>
    #define TT template<typename T>
    static const int Mod=998244353;
    TT inline void Swp(T &a,T &b) {T t=a;a=b;b=t;}
    TT inline void cmax(T &a,T b) {a=a>b?a:b;}
    TT inline void cmin(T &a,T b) {a=a<b?a:b;}
    TT inline void Madd(T &a,T b) {a=a+b>Mod?a+b-Mod:a+b;}
    TT inline void Mdel(T &a,T b) {a=a-b<0?a-b+Mod:a-b;}
    TT inline void Mmul(T &a,T b) {a=a*b%Mod;}
    TT inline void Mmod(T &a) {a=(a%Mod+Mod)%Mod;}
    TT inline T Cadd(T a,T b) {return a+b>=Mod?a+b-Mod:a+b;}
    TT inline T Cdel(T a,T b) {return a-b<0?a-b+Mod:a-b;}
    TT inline T Cmul(T a,T b) {return a*b%Mod;}
    TT inline T Cmod(T a) {return (a%Mod+Mod)%Mod;}
    TA inline void Madd(T &a,T b,Args... args) {Madd(a,Cadd(b,args...));}
    TA inline void Mdel(T &a,T b,Args... args) {Mdel(a,Cadd(b,args...));}
    TA inline void Mmul(T &a,T b,Args... args) {Mmul(a,Cmul(b,args...));}
    TA inline T Cadd(T a,T b,Args... args) {return Cadd(Cadd(a,b),args...);}
    TA inline T Cdel(T a,T b,Args... args) {return Cdel(Cdel(a,b),args...);}
    TA inline T Cmul(T a,T b,Args... args) {return Cmul(Cmul(a,b),args...);}
    TT inline T qpow(T a,T b) {int res=1; while(b) {if(b&1) Mmul(res,a); Mmul(a,a); b>>=1;} return res;}
    TT inline T qmul(T a,T b) {int res=0; while(b) {if(b&1) Madd(res,a); Madd(a,a); b>>=1;} return res;}
    TT inline T spow(T a,T b) {int res=1; while(b) {if(b&1) res=qmul(res,a); a=qmul(a,a); b>>=1;} return res;}
    TT inline void exgcd(T A,T B,T &X,T &Y) {if(!B) return X=1,Y=0,void(); exgcd(B,A%B,Y,X),Y-=X*(A/B);}
    TT inline T Ginv(T x) {T A=0,B=0; exgcd(x,Mod,A,B); return Cmod(A);}
    #undef TT
    #undef TA
}
using namespace MTool;

inline void file()
{
    freopen(".in","r",stdin);
    freopen(".out","w",stdout);
    return;
}

bool Mbe;

namespace LgxTpre
{
    static const int MAX=2010;
    static const int inf=2147483647;
    static const int INF=4557430888798830399;
    static const int mod=1e9+7;
    static const int bas=131;

	int n,q,ans[MAX*100];
	int x,y,z;
	
	vector<pii> G[MAX];
	vector<pair<int,pii>> Q[MAX];
	
	int in[MAX],out[MAX],tot;
	int fa[MAX],dis[MAX],pre[MAX],suf[MAX];
	int del,all;

    inline void lmy_forever()
    {
    	auto dfs=[&](auto dfs,int now,int father)->void
    	{
    		in[now]=tot++,fa[now]=father;
    		for(auto [to,val]:G[now]) if(to!=father) dis[to]=dis[now]+val,dfs(dfs,to,now);
    		out[now]=tot;
		};
    	
		read(n,q),memset(ans,-1,sizeof ans);
		for(int i=1;i<n;++i) read(x,y,z),G[x].eb(mp(y,z)),G[y].eb(mp(x,z)),all+=z;
		all<<=1;
		for(int i=1;i<=q;++i) read(x,y,z),Q[x].eb(mp(i,mp(y,z)));
		for(int i=1;i<=n;++i) if(Q[i].size())
		{
			tot=0,dis[i]=0,dfs(dfs,i,0);
			for(int j=1;j<=n;++j) pre[in[j]+1]=dis[j],suf[in[j]]=dis[j];
			for(int j=1;j<=n;++j) cmax(pre[j],pre[j-1]);
			for(int j=n;j>=1;--j) cmax(suf[j],suf[j+1]);
			for(auto [id,lim]:Q[i])
			{
				int key=lim.fi,trap=lim.se;
				if(in[trap]<=in[key]&&in[key]<out[trap]) continue;
				ans[id]=INF,del=max(pre[in[key]],suf[in[key]]);
				while(1)
				{
					cmin(ans[id],all+2*dis[key]-del);
					if(in[key]<=in[trap]&&in[trap]<out[key]) {ans[id]-=2*dis[key]; break;}
					del=max(pre[in[key]],suf[out[key]]),key=fa[key];
				}
			}
		}
		for(int i=1;i<=q;++i) if(ans[i]==-1) puts("impossible"); else write(ans[i],'\n');
        return;
    }
}

bool Med;

signed main()
{
//  file();
    fprintf(stderr,"%.3lf MB\n",abs(&Med-&Mbe)/1048576.0);
    int Tbe=clock();
    LgxTpre::lmy_forever();
    int Ted=clock();
    cerr<<1e3*(Ted-Tbe)/CLOCKS_PER_SEC<<" ms\n";
    return (0-0);
}