自动搬运

查看原文

来自洛谷，原作者为

	lw21144 山外青山楼外楼，唱跳 rap 打篮球，23 年退役 OIER 兼音游人，rks15.8 + ptt12.0

搬运于2025-08-24 22:48:23，当前版本为作者最后更新于2023-07-03 19:26:51，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

P9438『XYGOI round1』好多数

题目传送门，博客阅读更佳。

这是一道组合数学的好题，赛时调炸了，有点可惜，来补篇题解。

Subtask 1, 2

对 $n$ 分解质因数后直接暴力搜索，记录 $1$ 到 $10^6$ 中每个数在树中出现了几次，直接输出即可。

Subtask 3

本 Subtask 中保证 $n$ 是质数 $p$ 的 $k$ 次幂，以 $p=2,k=5,n=p^k=32$ 为例建立下图：

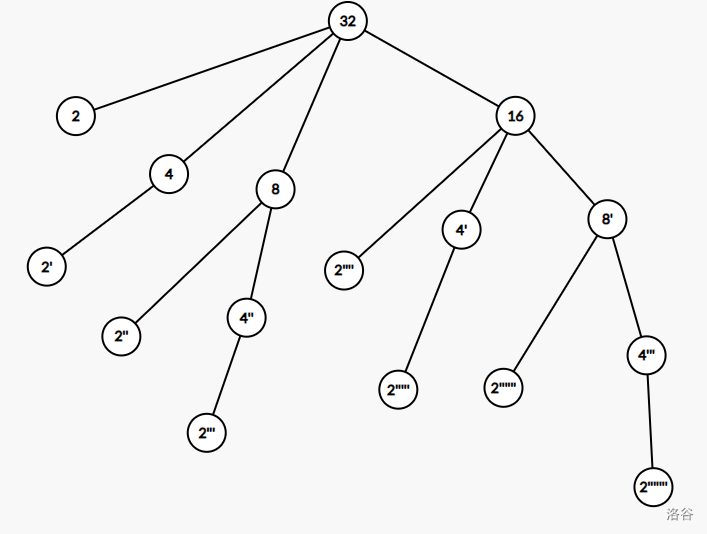
画的不是很好

观察此图，我们发现：

• 以 $2=2^1$ 为根的子树中仅有根节点 $2=2^1$。

• 以 $4=2^2$ 为根的子树中，除根节点外还有一个以 $2=2^1$ 为根的子树。

• 以 $8=2^3$ 为根的子树中，除根节点外还有两个分别以 $2=2^0,4=2^1$ 为根的子树。

据此，我们可以推断，以 $2^j$ 为根的子树，除根节点外相当于把 $2^i(0<i<j)$ 的子树复制了一遍，如上图。

接下来推广到一般，把 $2$ 换成任意质数 $p$，考虑出现次数。

对于 $p^i$，它将在 $p^i$ 的子树中出现在根节点，在 $p^{i+1}$ 的子树中出现在 $p^i$ 的子树中的 $1$ 次，在 $p^{i+2}$ 的子树中出现在 $p^i$ 的子树和 $p^{i+1}$ 的子树中，共 $2$ 次。

以此类推，因为 $p^k$ 最大符合条件的因数为 $p^{k-1}$，所以可得 $p^i$ 在整棵树中出现次数 $s$ 为：

$$s = 1+2^{(i+1)-i-1}+2^{(i+2)-i-1}+2^{(i+3)-i-1}+\cdots+2^{(k-1)-i-1} $$

即：

$$s=1+2^0+2^1+2^2+\cdots+2^{k-i-2}=1+\sum\limits_{j=0}^{k-i-2}2^j=2^{k-i-1} $$

所以只需特判每个问题中的 $x$ 是否为 $n$ 的因数，再直接代入计算即可。

Subtask 4

终于来到正解了。先看题目中给出的这张图：

我们发现：$24=2^3\times3^1$，分解质因数后仅有 $1$ 个 $3$，但是 $3$ 在图中却出现了 $4$ 次。

观察根节点到每个 $3$ 节点的路径：

• $24-3$；
• $24-6-3$；
• $24-12-3$；
• $24-12-6-3$；

可以发现，$24$ 到 $3$ 的路径中是这样的：

• $24-(÷8)-3$；
• $24-(÷4)-6-(÷2)-3$；
• $24-(÷2)-12-(÷4)-3$；
• $24-(÷2)-12-(÷2)-6-(÷2)-3$；

这相当于分多次除去两数的商 $8$，而除去的次数是可以随意的。

考虑 dp，设 $n$ 分解质因数后，总共有 $t$ 个质因数。

对于 $n=\prod\limits_{i=1}^{t}{a_i^{b_i}}$ 和读入的 $x=\prod\limits_{i=1}^{t}{a_i^{h_i}}$，它们的商为相同底数的幂相减的结果，即 $\prod\limits_{i=1}^{t}{a_i^{b_i-h_i}}$。

设 $f_i$ 表示花费 $i$ 次除掉这个商，也就相当于总共有 $sum=\sum\limits_{j=1}^{t}{b_j-h_j}$ 个数，将这些数分成 $i$ 段除去。

根据隔板法，可得状态转移方程式：

$$f_i=\prod\limits_{j=1}^{t}C_{b_j-h_j+i-1}^{i-1}$$

但是这样就会出现问题，还是上图的那个例子。

手模一下样例，当 $n=24=2^3\times 3^1,x=3=2^0\times 3^1$ 时，易得 $t=2;\ a_1=2,b_1=3,h_1=0;\ a_2=3,b_2=1,h_2=1$。

令 $i=2$，则根据上式可算出：$f_2=C_{3-0+2-1}^{2-1}\times C_{1-1+2-1}^{2-1}=C_4^1\times C_1^1=4\times 1=4$。

但是，由图中可以看出，两步变成 $3$ 的仅有 $24-6-3$ 和 $24-12-3$ 的 $2$ 种方案，与计算出的 $4$ 种方案不符。

进一步分析可以发现，多出的 $2$ 种方案分别是是 $24-24-3$ 和 $24-3-3$，相当于有一步是除以 $1$ 的无用步。

因此在状态转移方程式中，需要减去所有包含无用步的情况。

设在 $i$ 状态时（即分成 $i$ 段时）有 $j$ 步的无用步，那么：

• 这 $j$ 步的选择方式有 $C_i^j$ 种；
• 这 $j$ 步放在各个因数位置中的方式有 $f_j$ 种；

因此，根据乘法原理得无用步数为 $C_i^j\times f_j$ 种，最终的状态转移方程式：

$$f_i=\prod\limits_{j=1}^{t}C_{b_j-h_j+i-1}^{i-1}-\sum\limits_{j=1}^{i-1}{C_i^j\times f_j} $$

显然，最终答案 $ans$ 为分任意次除去两数的商的方案数之和，即：

$$ans=\sum\limits_{i=1}^{sum}{f_i}$$

时间复杂度 $O(q\times t^2)$，由于 $\sum{b_i}\leq 5000$，所以除掉次数的总上限不会超过 $5000$，在 $2$ 秒的时限下可以通过此题。

一些注意事项

• 组合数计算时求乘法逆元，要注意 $0$ 的逆元情况。

• 求 $f_i$ 时要做乘法，记得要全部初始化为 $1$。

• 注意 $q$ 个询问是独立的，要记得清空数组。

别问我为什么知道这些

AC code

本代码包含了每个 subtask 的解法，供大家参考。

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod=998244353;
int n,q,xx,yy,a[1000010],b[1000010],jc[1000010],ppow[1000010],p[1000010];

inline void Fre_open(){
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
}

namespace Fast_Read_And_Print{
	inline int read(){ //快读快写 
		int cnt=1,h=0; char ch=getchar();
		while(ch<'0'||ch>'9') cnt=(ch=='-')?-1:1,ch=getchar();
		while(ch>='0'&&ch<='9') h=h*10+(ch^48),ch=getchar();
		return h*cnt;
	}
	inline void print(int x){
		if(x<0) putchar('-'),x=-x;
		x>9?print(x/10),putchar((x%10)^48):putchar((x%10)^48);
	}
}
using namespace Fast_Read_And_Print;

namespace Bao_Li{ //暴力解法 
	inline void dfs(int x){
		p[x]++; //标记一次因数 
		for(int i=2;i<=sqrt(x);i++){
			if(x%i==0&&i*i==x) dfs(x/i);
			else if(x%i==0) dfs(i),dfs(x/i);
		}
		return;
	}
	inline void Solve_1(int sum){
		dfs(sum); //暴力搜索出现次数 
		while(q--){ //直接输出预处理的个数 
			xx=read(),print(p[xx]),putchar(32);
		}
	}
}

inline int quick_pow(int x,int y){
	if(y<0) return 1; int s=1;
	while(y){ //快速幂板子 
		if(y&1) s=(s*x)%mod;
		x=(x*x)%mod,y>>=1;
	}
	return s%mod;
}

namespace Sub_3{ // n 是质数的幂 
	inline void Solve_2(){
		while(q--){
			int x=read(),y=0,flag=0;
			if(x==1){ //题目说不会出现 1，直接特判 
				print(0),putchar(32); continue;
			}
			while(x>1){
				if(x%a[1]!=0&&x!=1){
					flag=1; break; //不存在这个因数 
				}
				x/=a[1],y++;
			}
			if(flag==1){
				print(0),putchar(32); continue;
			}
			int sum=quick_pow(2,b[1]-y-1);
			print(sum),putchar(32);
		}
	}
}

namespace Sub_4{ //正解 
	inline void init(){
		//预处理每个数的阶乘以及其逆元 
		jc[0]=1,ppow[0]=1; // 0 比较特殊，单独拿出来 
		for(int i=1;i<=1000005;i++){
			jc[i]=(jc[i-1]*i)%mod,ppow[i]=quick_pow(jc[i],mod-2);
		}
	}
	inline int C(int n,int m){
		if(n<m) return 0; //组合数计算，注意逆元 
		else return (((jc[n]*ppow[m])%mod)*ppow[n-m])%mod;
	}
	int h[1000010],f[1000010];
	inline void Solve_3(){
		init(); // printf("114514\n");
		while(q--){
			int cnt=read();
			memset(h,0,sizeof(h));
			memset(f,0,sizeof(f));
			if(cnt==1){ //题目说不会出现 1，直接特判 
				print(0),putchar(32); continue;
			}
			for(int i=1;i<=n;i++){
				while(cnt%a[i]==0&&h[i]<=b[i]) cnt/=a[i],h[i]++;
				// 对 cnt 分解质因数，cnt=(a[1]^h[1])*(a[2]^h[2])*...*(a[n]^h[n]) 
			}
			int flag=0,sum=0,anss=0;
			for(int i=1;i<=n;i++){
				if(b[i]!=h[i]) flag=1; sum+=b[i]-h[i];
			} 
			if(cnt>1){
				print(0),putchar(32); continue; // cnt 不能被 n 整除 
			}
			if(flag==0){ 
				print(1),putchar(32); continue;
				//每个幂都相等，此时 cnt 就是 n 本身，仅在根节点出现一次 
			}
			// dp
			for(int i=1;i<=sum;i++){
				f[i]=1; //因为要做乘法，所以初始化为 1 
				for(int j=1;j<=n;j++){
					f[i]=(f[i]*C(b[j]-h[j]+i-1,i-1))%mod;
					// printf("%lld %lld %lld\n",b[j]-h[j]+i-1,i-1,C(b[j]-h[j]+i-1,i-1));
				}
				// printf("\n");
				for(int j=1;j<i;j++){
					f[i]=(f[i]-((C(i,j)*f[j])%mod)+mod)%mod;
					// printf("%lld %lld %lld\n",i,j,C(i,j));
				}
				anss=(anss+f[i])%mod; //统计答案 
				// printf("%lld %lld\n",f[i],anss);
			}
			print(anss),putchar(32);
		}
	} 
}

signed main(){
	// Fre_open();
	while(1){ //读入 
		xx=read(),yy=read();
		if(xx==0&&yy==0) break;
		a[++n]=xx,b[n]=yy; 
	}
	int sum=1,flag=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=b[i];j++){
			sum*=a[i]; if(sum>1000000) flag=1,j=114514; //这里相当于 break 
		}
		if(flag) break;
	}
	q=read(); //读入询问次数 
	if(flag==0) Bao_Li::Solve_1(sum); //subtask 1,2 
	else if(flag==1&&n==1) Sub_3::Solve_2(); //subtask 3 
	else Sub_4::Solve_3(); //subtask 4 
    return 0;
} 

这是通过记录，最大耗时点 $866$ 毫秒。

求管理给过审吧

---

update 2024.10.24

修改了部分错误，优化了一些语句表达。