自动搬运

查看原文

来自洛谷，原作者为

	xs_siqi galgame 元老级玩家

搬运于2025-08-24 22:48:22，当前版本为作者最后更新于2023-07-02 16:19:13，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

赛时解出了。思路好想，维护细节较多的换根 dp。这道题考验了对换根 dp 模型基本掌握。

正文：本题如何运用换根 dp

换根 dp 其实是有模板的。

我总结了一下，一般情况的换根 dp 就是的过程通常是两遍 dfs，并在写题的过程中思考以下问题：

• 两次 dfs 前先维护两次 dfs 需要的信息

• 第一遍维护第二次换根过程中需要维护的信息，以及以任意一个点为根（通常为了方便取 $1$ 号节点为根）如何得到原始 $f$ 值（即其原始方程）

• 第二遍换根的转移方程

• 两遍 dfs 后输出的值

我们尝试使用这个模板来解决这个问题。

这题为什么是换根 dp？

此题题意可以转化为：随意确定一个点为根节点，然后计算其他节点到根节点的长度和。于是可以用换根 dp 解决。

dfs 前：两遍 dfs 前维护什么？

首先观察边权是如何得出的：两个节点点权按顺序拼起来。如何将两数拼起来？令后一个节点为 $x$，那么它的位数便是它对 $10$ 取对数。所以我们得出第一个需要维护的就是一个数对 $10$ 取对数的值（当然，你也可以不维护，直接用系统自带函数一步得出也可以）。

回到“如何拼起来”的问题，令原有数为 $x$，要拼的数为 $y$，拼起来的代价是 $x\times 10^{num(y)}+y$。 $num$ 函数是该数的位数。举个例子，将 $5$ 与 $6$ 拼起来，$6$ 的位数是 $1$，所以是 $5\times 10+6=56$。由此可见，我们还需维护 $10$ 的次方倍。 由数据范围可知，我们只需要维护到 $10^9$ 即可。

总结：维护 $10$ 的次方倍与各个数位数。

第一遍 dfs：维护什么？原始方程是什么？

首先我们明晰这样一点：每个点到根节点的总长度，可以转化为每条边的边权乘由几个点走过这条边。即计算贡献。

这样转化有什么妙处？可以向父亲转移状态了。

我们看到我们转化后，需要记录有几个点经过一条边，显然就是这个点是多少点的祖先，也就是这个点的 $size$。于是我们得出第一次 dfs 需要维护每个点的 $size$ 信息。

然后考虑原始转移方程。令 $f_u$ 为 $u$ 节点的所有孩子到 $u$ 节点的总路径长度之和，那我们可以得到以下方程：

$f_u=f_v\times 10^{num(u)}+p_u\times size_v$

解释一下这个方程：$u$ 是 $v$ 的父节点，$p_u$ 指的是 $u$ 节点的权值，$p_u\times size_v$ 表示有 $size_v$ 个数经过这条边。

总结：维护 $size$ 信息，并使用上述方程求得其他点（包括根节点，此题中点到自己本身也有距离）到根节点的距离之和。

第二次 dfs：如何运用维护的信息？方程是什么？

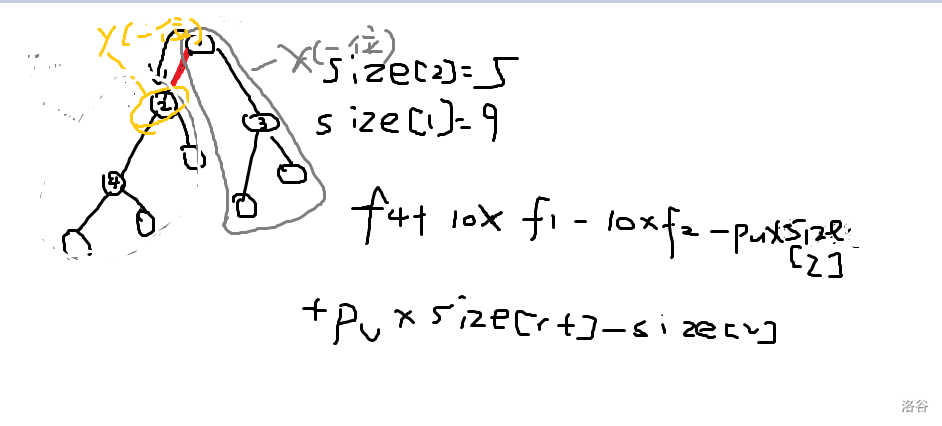
如何列方程？我们从最简单的情况入手。如图是 $1$ 节点向 $2$ 节点下移的过程。

• 首先考虑节点 $2$ 的子树部分。我们发现我们需要节点 $4$ 的 $f$ 值作为换根后的总值。这个值在第一次 dfs 已经求过了，直接调用 $f_4$ 即可。

• 然后考虑节点 $2$ 的非其子树部分。有人可能认为可以直接调用 $f_3$ 的值，这是不可行的。请注意，树不一定是二叉树，假如是菊花图的情况，可以把这个解法卡到 $n^2$。

• 于是很自然能想到这个思路：将根节点的 $f$ 值减去 $2$ 好点的 $f$ 值。如图（图中算式有误，请手动在 $10\times f_1$乘号后加一个左括号，第一行最右边加上右括号），考虑最简单的情况，令 $f_2$ 为一位数，$f_1$ 也为一位数，那么除了 $f_2$ 以外的 $f$ 值显然是 $f_1-10\times f_2$。

两边 $f$ 值问题已经解决。现在我们解决换根对于边的贡献问题。

• 首先，$1$ 节点下所有节点及它自己少了红边。所以应为 $size_2\times p_u$。

• 其次，除了 $2$ 节点子树以外所有节点都多了红边，所以应为 $p_v\times (size_{rt}-size_v)$。

那么整个方程过程就结束了。然后总结以下就是这个方程：

$f_v=f_v+10^{num(v)}\times(f_u-f_v\times 10^{num(u)}-p_u\times size_v)+(p_u\times (size_{rt}-size_v))$。

两次 dfs 后：答案是什么？

$f$ 值表示每个节点以下的点（包括自身）到其距离。那么显然就是 $f$ 数组中所有元素的和。

需要注意的细节

考虑到本题数据较大，所以要时时注意取模操作。还有例如刚刚的部分换根方程的处理：

$(f_u-f_v\times 10^{num(u)}-p_u\times size_v)$

若时时取模，这个地方可能会变成负数。所以我们可以直接加模数，不影响取模后结果，即变成：

$(f_u+mod\times 5-f_v\times 10^{num(u)}-p_u\times size_v)$

取模后结果是一致的。

附代码：

#include<bits/stdc++.h>
#define int unsigned long long
using namespace std;
const int maxn=2e6+5;
const int mod=998244353;
int n,p[maxn],wei[maxn],ship[15],ans,f[maxn];
int fir[maxn],nxt[maxn],son[maxn],tot,q,siz[maxn];
inline void add(int x,int y){son[++tot]=y;nxt[tot]=fir[x];fir[x]=tot;}
inline void dfs1(int u,int fa){
	siz[u]=1;f[u]=p[u];//点到其本身也有距离
	for(int i=fir[u];i;i=nxt[i]){
		int v=son[i];
		if(v==fa)continue;
		dfs1(v,u);
		siz[u]+=siz[v];//维护size
		f[u]+=f[v]*ship[wei[u]]%mod+p[u]*siz[v]%mod,f[u]%=mod;}}
inline void dfs2(int u,int fa){
	for(int i=fir[u];i;i=nxt[i]){
		int v=son[i];
		if(v==fa)continue;
		f[v]=f[v]+(ship[wei[v]]%mod*((f[u]+mod*5)-f[v]*ship[wei[u]]%mod-p[u]*siz[v]%mod)%mod+(p[v]*(siz[1]-siz[v]))%mod)%mod;//只是刚刚推出来的方程多加了几个%mod
		f[v]%=mod;
		ans+=f[v],ans%=mod;
		dfs2(v,u);}}
signed main(){
	scanf("%lld",&n);
	ship[0]=1;
	for(int i=1;i<=13;i++)ship[i]=ship[i-1]*10,ship[i]%=mod;//shi p，10的几次方，不是ship小船
	for(int num,i=1;i<=n;i++){
		scanf("%lld",&p[i]);num=p[i];
		if(num==0)wei[i]=1;//wei就是位数
		else while(num)num/=10,wei[i]++;}
	for(int x,i=1;i<n;i++)scanf("%lld",&x),add(i+1,x),add(x,i+1);
	dfs1(1,0);dfs2(1,0);
	printf("%lld\n",(ans+f[1])%mod);//因为我的dfs过程只求除了f1以外的总和
	return 0;} 

后文：本题对换根 dp 的启示

本题只是在边权形式上进行了创新，增加细节，换根 dp 过程本质是不变的。

所以只要熟练掌握换根dp的常见技巧过程，以及提高细节处理能力，相信换根 dp 就是常规题了。