自动搬运

查看原文

来自洛谷，原作者为

	___w **

搬运于2025-08-24 22:48:06，当前版本为作者最后更新于2023-06-13 13:54:54，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

P9409 『STA - R2』交朋友

题意简述

有 $t$ 天，共 $n$ 个小朋友构成一张无向图，有的小朋友有毛绒玩具，有以下几个要求：

• 有毛绒玩具的小朋友会选择一个在这一天和他坐在一起的且没有毛绒玩具的小朋友。
• 每个人至多只有一个毛绒玩具。

求初始时最多可以有多少小朋友有毛绒玩具，使得不存在小朋友送不出毛绒玩具。

题目分析

因为有毛绒玩具的小朋友要把毛绒玩具递给其他人，就像网络流中的每一个点能流则就流出去一般，所以考虑网络流。有 $t$ 天，每天的小朋友的状态各不相同，因为可能今天可以给这个人但每天就可能不可以给这个人，所以我们把所有的点分为 $t+1$ 层，每一层有 $n$ 个节点，表示哪一天的哪个小朋友。建立超级源点，连接第 $1$ 天的每个小朋友，容量为 $1$，表示每个小朋友可以拥有一个毛绒玩具。再建立超级汇点，从第 $t+1$ 天的小朋友连接到超级汇点，容量为 $1$，表示最后的毛绒玩具交上去，就可以得到最多可以有多少小朋友有毛绒玩具了。至于两个相邻的小朋友 $u,v$，只需要把今天的 $u$ 与明天的 $v$ 及今天的 $v$ 与明天的 $u$ 建条边，容量为 $1$。如下图所示，为样例 $2$ 的图。

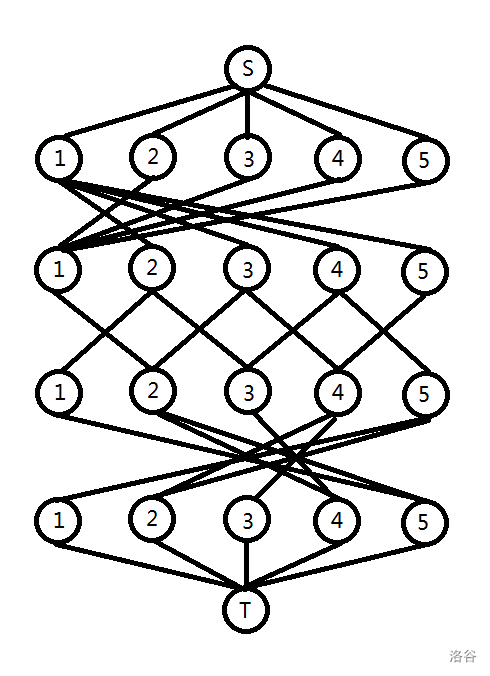
但是呢，题目还说到每个人至多只有一个毛绒玩具，所以考虑把每个小朋友拆成两个点，分为入点和出点，从入点连接到出点，容量为 $1$。这样就可以保证每个小朋友的每一天就最多只有一只毛绒玩具了。建完模型以后得出来的最大流即为答案，就可以套用网络流模板了，代码如下。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 7e6, M = 2e6, inf = 1e9;
struct edge {
	int to, next, w;
} e[M];
int T, n, m, s, t, ans, tot = 1, d[N], cur[N], head[N];
void add(int x, int y, int z) {
	e[++tot] = (edge){y, head[x], z}, head[x] = tot;
	e[++tot] = (edge){x, head[y], 0}, head[y] = tot;
}
bool bfs() {
	memset(d, 0, sizeof(d)), d[s] = 1;
	queue <int> q; q.push(s);
	while (!q.empty()) {
		int x = q.front(); q.pop();
		for (int i = head[x]; i; i = e[i].next)
			if (e[i].w && !d[e[i].to]) {
				q.push(e[i].to); d[e[i].to] = d[x]+1;
				if (e[i].to == t) return 1;
			}
	}
	return 0;
}
int dfs(int x, int flow) {
	if (x == t) return flow;
	int k, res = 0;
	for (int i = cur[x]; i && flow; i = e[i].next) {
		cur[x] = i; int y = e[i].to;
		if (e[i].w && d[y] == d[x]+1) {
			k = dfs(y, min(flow, e[i].w));
			if (!k) d[y] = 0;
			e[i].w -= k, e[i^1].w += k;
			res += k, flow -= k;
		}
	}
	return res;
}
int id(int i, int x, int d) { return i*n*2+x*2+d; }
int main() {
	cin >> T >> n;
	s = (T+1)*n*2+2, t = s+1;
	for (int k = 0; k <= T; ++k)
		for (int i = 1; i <= n; ++i)
			add(id(k, i, 0), id(k, i, 1), 1);//入点和出点 
	for (int i = 1; i <= n; ++i) add(s, id(0, i, 0), 1), add(id(T, i, 1), t, 1);//超级源点和超级汇点 
	for (int k = 0, u, v; k < T; ++k) {
		cin >> m;
		while (m--) {
			cin >> u >> v;
			add(id(k, u, 1), id(k+1, v, 0), 1);
			add(id(k, v, 1), id(k+1, u, 0), 1);
			//由于是无向图，所以要建两条边 
		}
	}
	while (bfs()) {
		memcpy(cur, head, sizeof(head));
		ans += dfs(s, inf);
	}
	cout << ans;
	return 0;
}