自动搬运

查看原文

来自洛谷，原作者为

	ix35 垒球

搬运于2025-08-24 22:47:58，当前版本为作者最后更新于2023-06-03 23:32:48，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

橙垒球

定义 $Suf(i)$ 表示（$w$ 的）以 $i$ 开头的后缀。

我们首先将字典序反转，那么最大后缀就变成了最小的不是其他后缀的前缀的后缀。

定义 1：若 $w$ 小于它的所有真后缀，则称 $w$ 是 Lyndon 串；若 $v$ 是 Lyndon 串且 $w=v^kv'$，其中 $v'$ 为 $v$ 的前缀，则称 $w$ 是近似 Lyndon 串；若 $v$ 是 Lyndon 串且 $w=v^k$，则称 $w$ 是 Necklace。

定义 2：定义一个后缀 $Suf(k)$ 是 Significant Suffix，当且仅当存在一个 $v$ 使得 $Suf(k)+v=\min_i(Suf(i)+v)$。

考虑 Duval 算法求最大后缀，不难发现 $w$ 的最大后缀就是 Duval 算法第一次运行完 $w$ 的末尾时对应的近似 Lyndon 串，同时它是 $w$ 的最长的 Significant Suffix。

设 $a_i=1,\ a_{i+1}=p>1$，于是：$w[1\ldots i]$ 是近似 Lyndon 串，$w[p\ldots i+1]$ 也是近似 Lyndon 串。

模拟 Duval 算法可知，$w[p\ldots i]$ 是 $w[1\ldots i]$ 的前缀（也可以根据 Significant Suffix 的结构发现），同时下一个字符 $w_{i-p+2}$ 必须大于 $w_{i+1}$（否则 $a_{i+1}$ 也等于 $1$ 了））。

由于我们现在希望字典序最小，所以最佳的选择就是让 $w_{i-p+2}$ 比 $w_{i+1}$ 恰好大 $1$，而后面的部分 $w[i-p+3\ldots i]$ 可以重复前面的模式 $w[1\ldots i-p+2]$ 进行循环。由于 $w[p\ldots i+1]$ 是近似 Lyndon 串，所以把它的最后一个字符增大 $1$ 得到一定就是 Lyndon 串，于是 $w[1\ldots i]$ 确实是一个 Lyndon 串的若干次方加上一个前缀，符合近似 Lyndon 串的要求。

大致结构如下（每种颜色是一个字符，$+1$ 表示比对应颜色字符恰好大 $1$ 的字符）：

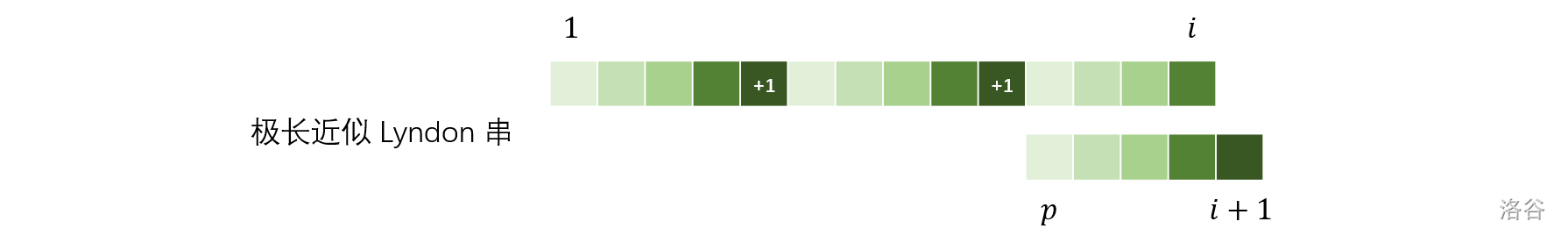
但是上面的只是一种情况，如果 $w[1\ldots p-1]$ 不能表示成若干个完整的循环，那么就会出问题：Duval 算法加入 $w_{i+1}$ 后会把前面的完整循环截断，但是并不会恰好截到 $p$ 这个位置。为了让它恰好截到 $p$ 这个位置，我们可以让 $w_{p-1}$ 增大 $1$，这样一来前缀 $w[1\ldots p-1]$ 自成一个 Lyndon 串，截断时自然会把它截去。

大致结构如下：

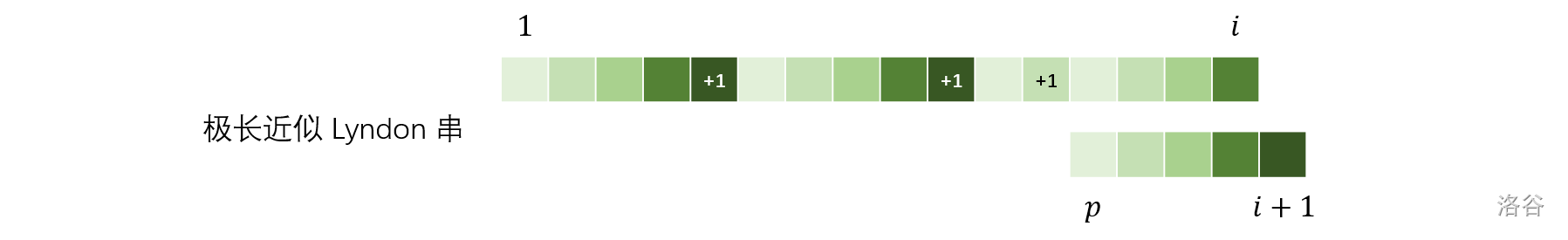
考虑何时会无解：如果 $w[1\ldots p-1]$ 比 $w[p\ldots i+1]$ 还要短，那么第一个循环都没办法完全填完，这时就会无解（这个结论有另外两种理解：一种是 Duval，由于截断后保留的是前一段 Lyndon 因子的前缀，所以截掉的长度一定大于一半；另一种是 Significant Suffix，$w[1,i]$ 和 $w[p,i]$ 都是 Significant Suffix，因此前者的长度大于后者的两倍）。

如果我们构造完了后缀 $Suf(p)$，就可以利用上面的方法得到 $w[1\ldots p-1]$，同时由于 $w[1\ldots p-1]$ 的前缀是 $w[p\ldots i+1]$，所以最小化 $w$ 就等价于最小化 $w[p\ldots |w|]$，优化目标一样，所以可以直接递归后缀 $Suf(p)$。当然，这和从后往前贪心是等价的。

时间复杂度为 $O(n)$。