自动搬运

查看原文

来自洛谷，原作者为

	ix35 垒球

搬运于2025-08-24 22:47:58，当前版本为作者最后更新于2023-06-03 23:33:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

白鹭兰

我们首先考虑，如何判断是否有 $k=1$，即是否存在一个点的排列，使得所有前缀和后缀的导出子图连通。将这个过程看成每次染黑一个点，时刻保证当前黑点和白点的导出子图都是连通的。

考虑图的圆方树，如果所有点双连通分量没有构成一条链，就说明存在一个割点 $x$ 使得删去它后图分成至少三个连通块，设其中三个连通块为 $C_1,C_2,C_3$，由于加入 $x$ 前黑白点导出子图都是连通的，所以 $C_1,C_2,C_3$ 至少有两个是纯白的（因为 $x$ 是白的），加入 $x$ 后这两个纯白的部分就一定不连通了，这说明一定不存在一个可行的方案。

后面我们会构造证明，只要点双连通分量排成一条链，就一定有 $k=1$ 的解。

下面考虑如何求最小的 $k$，使得存在一种方案每次染黑至多 $k$ 个点，任何时刻黑白点导出子图都连通。我们设第一个被染黑的点（第一批 $V_1$ 里任选一个）和最后一个（最后一批里任选一个）被染黑的点分别是 $x,y$，不妨设它们都是圆方树的叶子（否则可以调整），考虑路径 $x\to y$。

对于 $x\to y$ 上的某个圆点 $z$，事实上根据前面的讨论，$z$ 连同其不在 $x\to y$ 路径上的所有子树内的点都必须在同一次操作中被染黑，否则可以由和上面一样的方法导出矛盾。

同理，对于 $x\to y$ 上的某个方点 $u$，对于其每一个不在 $x\to y$ 路径上的儿子（圆点）$v$，$v$ 在 $x\to y$ 路径外侧的子树中的所有点必须在同一次操作中被染黑。

这样我们得到了若干个必须同时被染黑的集合，称为关键集合，它们的大小的最大值就是这一组 $(x,y)$ 对应的 $k$ 的最小值。下图展示了一个例子，每个红框中的部分是每个关键集合：

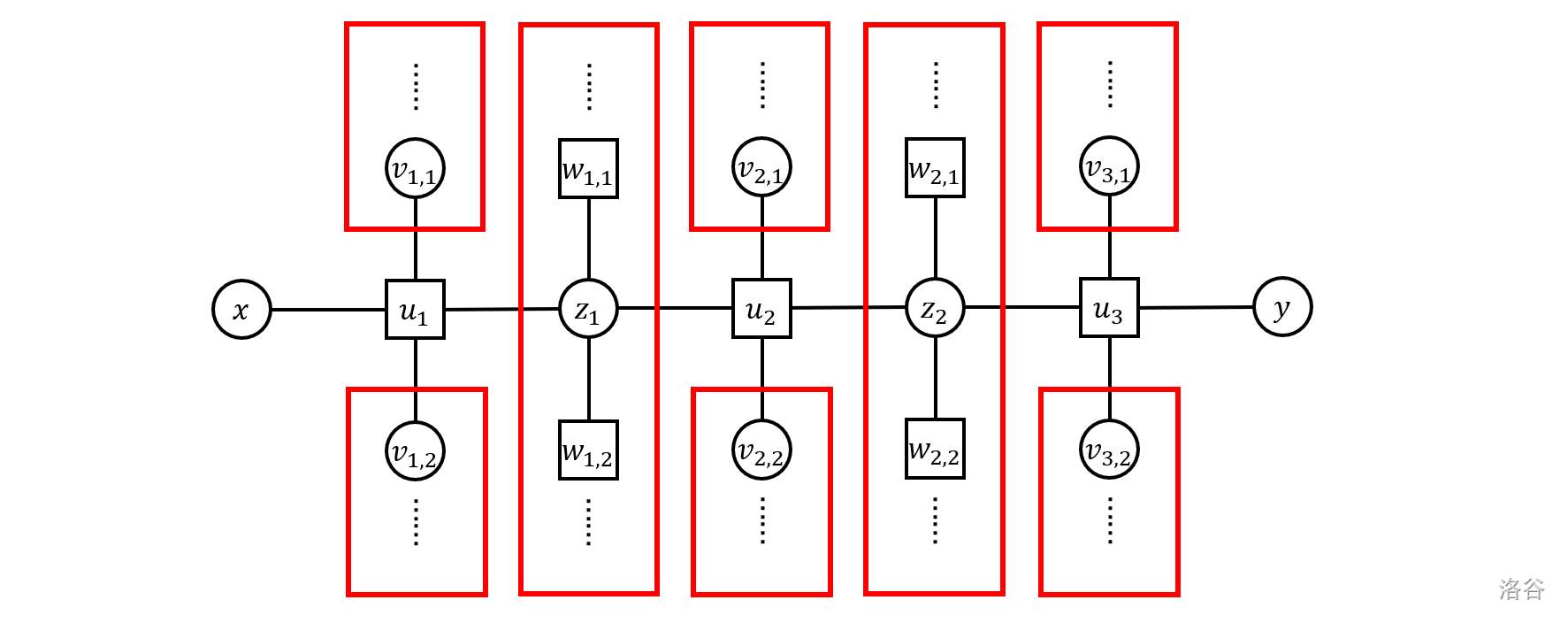
但是暴力枚举 $x,y$ 的复杂度太高，尝试分析一些性质。

设 $x,y$ 的 LCA 是 $z$，且分别属于 $z$ 的儿子 $x_0,y_0$ 的子树，$x_0$ 到 $x$ 的路径为 $x_0\to x_1\to \ldots\to x_s=x$，那么我们证明：存在一种最优的 $x$，使得这个路径上任意两个相邻点都满足 $x_{i+1}$ 是 $x_i$ 的最大子树（$i\ge 1$）。

这是因为，设 $x_i$ 的最大子树是 $x'$，其大小为 $S$，如果 $x_{i+1}\ne x'$，则在 $x_i$ 处计算的贡献（$x_i$ 所在的关键集合大小）至少为 $S$，然而如果将 $x_{i+1}$ 调整为 $x'$，则在 $x_i$ 处计算的贡献一定会变小，而 $x_{i+1}$ 子树内算的贡献一定不会超过 $S$（因为整个子树大小只有 $S$)，因此一定不会更劣。

于是我们可以用树形 DP 来计算答案。设 $sn(x)$ 表示 $x$ 的最大子树，记 $f(x)$ 表示 $x\to sn(x)\to sn^2(x)\to \ldots$ 这条路径上的贡献。对于某个点 $z$，设其大小最大和次大的子树分别是儿子 $x,y$ 的子树，那么用 $\max(f(x),f(y),g(z,x,y))$ 更新答案即可，其中 $g(z,x,y)$ 表示 $z$ 这里的贡献（同上不难证明选择最大和次大的子树 $x,y$ 是最优的）。

上面我们已经解决了本题的第一部分，即圆方树上的部分，下一部分是构造答案，即一个点双连通分量内部怎么构造一种固定第一个染黑的点为 $x$，最后一个染黑的点为 $y$ 的每次染黑一个点的方案。

以 $x$ 为根，考虑 Tarjan 算法，对于每个点 $u$ 求出 DFS 树子树内通过返祖边可到达的最浅祖先 $low(u)$。考虑剥叶子，对于一个叶子 $u$，它有两个邻居 $f(u),low(u)$，我们可以在这两个点中的任意一个被染黑后立刻染黑 $u$，染黑 $u$ 与否并不会对剩余部分的连通性产生影响，所以这一定是合法的。

于是我们就从下往上考虑，对于每个点 $x$ 用 vector 维护一个后继列表 $L_x$，每次删一个叶子 $u$，就在 $L_{f(u)}$ 和 $L_{low(u)}$ 中在末尾插入 $u$。然后，我们染黑根结点 $x$。每当染黑一个点 $u$ 时，就从前到后依次递归染黑 $L_u$ 中的所有元素，这个过程中每个结点被染黑的顺序就是我们要求的答案。

但是上面我们没有考虑到 $y$ 要最后一个染黑，为此我们对算法稍加修改：剥叶子剥到 $y$ 的时候就不剥了，这样 $x\to y$ 路径上的点都会被保留，然后我们按照 $x\to y$ 的顺序依次染黑这些点。我们断言染黑 $y$ 时 $L_y$ 中的点已经全是黑的了，从而 $y$ 就是最后一个被染黑的：这是因为如果染黑 $y$ 时 $L_y$ 中还有没被染黑的点，就说明有一个点的所有（$y$ 以下的）祖先和后代都没有连到 $y$ 的祖先的返祖边，这说明 $y$ 是一个割点。

时间复杂度为 $O(m)$。