自动搬运

查看原文

来自洛谷，原作者为

	yemuzhe 烟波里成灰 也去得完美

搬运于2025-08-24 22:47:52，当前版本为作者最后更新于2023-07-31 21:49:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

此题解篇幅太长，请谨慎观看！

题目大意

• 有一个大小为 $n$ 的牌堆 $A$，牌堆中的数均为 $1 \sim n / 2$，且每个数恰好出现 $2$ 次。

• 刚开始有两个空栈。可以进行 $op$ 次操作，有两种操作：

  1. 可以把牌堆顶上的数放入一个栈中，如果该栈最上方的两个数相同，则自动消去这两个数。

  2. 如果两个栈顶的数相同，则可以消去这两个数。

• 构造一种操作方案，使得所有数都被消去。

• $2 \le n \le 1500$ 且 $n$ 为偶数。

解题思路

这题可用区间 dp 解决。

容易发现，第一种操作的后半句没什么用，因为可以改写成第二种操作来实现。

于是我们把相同的两个数放入不同的栈中，也避免了第一种操作的自动消除。

考虑牌堆中的一段区间 $[l, r]$。内部可以消去的肯定要消去，剩下的是不能消去的数，且按原牌堆顺序排列。

如图：（图中一种颜色的球代表一个数）

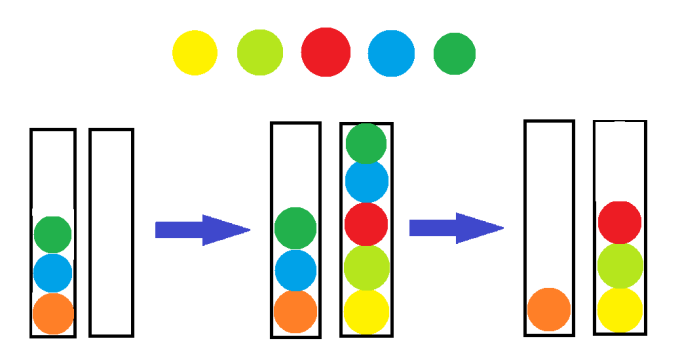
当然，也不一定像这样所有一起加入后再消除。

在 dp 时我们枚举 $[l, r]$ 内最后消去的数（可能一个或两个），然后分段处理。

我们把 $[1, l - 1]$ 中能和 $[l, r]$ 中的数配对的数称为「有用的数」。

这里有一条非常重要的性质：

「有用的数」一定都（要）堆在同一个栈的最顶部。

我们把这个栈称为「有用的栈」。如果没有「有用的数」则认为两个栈都是「有用的栈」。

这条性质的证明将会在「区间 dp」部分的末尾给出。请读者时刻牢记这一性质。

Part 1：预处理

在 dp 之前，我们需要预处理几个数组：$p, lx, ry, xl, ly, yr$。

• $p$ 数组

  $p _ i$ 记录的是值为 $A _ i$ 的另一个数的位置。可以用一个 $l$ 数组记录 $A _ i$ 上一次出现的位置处理。

  for (int i = 1; i <= n; i ++)
  {
      // 如果 A[i] 已经出现过，那么那么令 p[上一次出现的位置] = i 且 p[i] = 上一次出现的位置
      if (l[a[i]]) p[l[a[i]]] = i, p[i] = l[a[i]];
      l[a[i]] = i; // 用当前位置更新
  }
  

• $lx$ 数组

  $lx _ {l, r}$ 表示对于 $l \le i \le r$，最前面的满足 $p _ i > r$ 的 $i$。

  初始化 $lx _ {r + 1, r} = r + 1$（即无穷大），易得递推式 $lx _ {l, r} = \begin {cases} lx _ {l + 1, r} & (p _ l \le r) \\ \min \{lx _ {l + 1, r}, l\} & (p _ l > r) \end {cases}$。

  这个函数可以用来判断 $[l, r]$ 内的数是否可以全部消除（即 $lx _ {l, r}$ 是否大于 $r$）。

• $ry$ 数组

  $ry _ {l, r}$ 表示对于 $l \le i \le r$，最后面的满足 $p _ i < l$ 的 $i$。

  初始化 $ry _ {l, l - 1} = 0$（即负无穷大），易得递推式 $ry _ {l, r} = \begin {cases} lx _ {l, r - 1} & (p _ r \ge l) \\ \min \{lx _ {l, r - 1}, r\} & (p _ r < l) \end {cases}$。

  可以在 dp 时顺便处理，省去两维（就变成变量了）。

• $xl$ 数组

  $xl _ {l, r}$ 表示对于 $l \le i \le r$，最前面的 $p _ i$。

  初始化 $xl _ {l, l - 1} = l$，易得递推式 $xl _ {l, r} = \min \{xl _ {l, r - 1}, p _ r\}$。

  可以在 dp 时顺便处理，省去第一维（如果不是还要预处理 $yr$ 数组还可省去第二维）。

• $ly$ 数组

  $ly _ {l, r}$ 表示对于 $r < i \le n$，最前面的满足 $xl _ {l, r} < p _ i < l$ 的 $i$。

  考虑用树状数组实现。注意这里的树状数组的循环顺序有些不同，用来实现后缀查询。

  加入时只加 $p _ i < l$ 的。在 $p _ i$ 位置加入 $i$。

  查询时 $(xl _ {l, r}, n]$ 这一段区间的最小值，也可以查询 $[xl _ {l, r}, n]$。

  可以在 dp 时顺便处理，省去第一维。

  void modify (int p, int c) // 单点修改（其实是加入）
  {
      for (; p; p &= p - 1) tr[p] = min (tr[p], c);
      return ;
  }
  
  int ask (int p) // 区间（后缀）求最小值
  {
      int res = inf;
      for (; p <= n; p += p & -p) res = min (res, tr[p]);
      return res;
  }
  
  // int main ()
  
  for (int l = n; l; l --)
  {
      // ...
      memset (tr, 0x3f, sizeof tr);
  	for (int r = n; r >= l; r --)
      {
          ly[r] = ask (xl[r]); // 询问满足条件的最小 i
          if (p[r] < l) modify (p[r], r); // 加入当前 r
      }
      // ...
  }
  

• $yr$ 数组

  $yr _ {l, r}$ 表示对于 $l \le i \le r$，最后面的 $p _ i$。

  初始化 $yr _ {l, l - 1} = l$，易得递推式 $yr _ {l, r} = \max \{yr _ {l, r - 1}, p _ r\}$。

  可以在 dp 时顺便处理，省去两维（就变成变量了）。

这样我们就完成了所有的预处理。

Part 2：区间 dp

状态设计

记 $f _ {l, r}$ 为当一个栈是「有用的栈」时，能否删完 $[l, r]$ 内配对的部分并把剩下的堆在另一个栈。

同理记 $g _ {l, r}$ 为当一个栈是「有用的栈」时，能否删完 $[l, r]$ 内配对的部分并把剩下的堆在同一个栈。

考虑到可能没有剩余的，记 $both _ {i, j}$ 为当一个栈是「有用的栈」时，能否删完 $[l, r]$ 这部分。

容易发现 $both$ 其实是 $f$ 和 $g$ 共同的特殊情况。

注意「状态转移」部分中分界点的同 / 另一个栈是相对整个区间而言，而子区间的同 / 另一个栈是对子区间而言。

由于题目还要求具体方案，需要存三个数组 $pf, pg, pboth$，来记录转移的信息（具体见「状态转移」部分）。

根据「状态转移」部分可知，最终答案即 $both _ {1, n}$ 的过程仅与 $f, g, both$ 有关，故只设计设三种状态即可。

初始化

初始化 $f _ {i + 1, i} = g _ {i + 1, i} = both _ {i + 1, i} = 0$（$0 \le i \le n$）即可。

状态转移

• 第一种：$g \leftarrow f + f$

  概念

  

  如上图，我们选择最前面的满足 $p _ i > r$ 的 $i$ 即 $lx _ {l, r}$，然后把这个序列分成 $[l, i - 1]$、$i$ 和 $[i + 1, r]$ 三段。

  对于 $[l, i - 1]$ 这段，把它们放进另一个栈（右边）。

  对于 $i$，把它放进同一个栈（左边），它不会产生任何消除（和它配对的在 $r$ 后面）。

  对于 $[i + 1, r]$，把它们放进另一个栈（这时是左边），这时它们会把 $[l, i - 1]$ 这部分剩下的全部消掉。

  为什么这时候另一个栈是左边呢？因为左边的栈已经被 $i$ 堵住了，相当于是空栈（没用），但右边的栈很可能是「有用的栈」。

  这样我们就不会在另一个栈（右边）剩东西，从而实现了 $g$ 的转移。

  为什么 $i$ 一定是最后消除的呢？

  如果分界点为 $i$，那么 $[i + 1, r]$ 的剩余部分都会叠在 $i$ 上面（堵住了），而 $[l, i - 1]$ 没有剩余；

  如果分界点不为 $i$，那么 $i$ 就会剩在另一个栈无法消去，不符合 $g$ 的定义。

  读者不妨可以模拟一下上图的具体过程。

  前提

  首先得保证存在这么一个 $i$，也就是存在 $i$ 使得 $p _ i > r$，即 $lx _ {l, r} \le r$。

  其次要保证 $[i + 1, r]$ 与前面的 $[1, l - 1]$ 无关。

  也就是 $[l, r]$ 最后面的满足 $p _ j < l$ 的 $j$ 不在 $[i + 1, r]$ 中，即 $ry _ {l, r} \le i$（也可 $ry _ {l, r} < i$）。

  转移

  放入 $i$ 一定是合法的。所以只需判 $f _ {l, i - 1}$ 和 $f _ {i + 1, r}$ 的合法性即可。

  这时 $pg$ 数组不需记录信息，具体见「查找每个数放入的栈」。

  if (lx[l][r] <= r) // 第一种情况
  {
      now = lx[l][r];
      if (ry < now) g[l][r] = f[l][now - 1] & f[now + 1][r];
  }
  

• 第二种：$f \leftarrow g + f$

  概念

  

  如上图，我们选择最前面的满足 $p _ i > r$ 的 $i$ 即 $lx _ {l, r}$，然后把这个序列分成 $[l, i - 1]$、$i$ 和 $[i + 1, r]$ 三段。

  对于 $[l, i - 1]$ 这段，把它们放进同一个栈（左边）。

  对于 $i$，把它放进另一个栈（右边），它不会产生任何消除。

  对于 $[i + 1, r]$，把它们放进另一个栈（右边），这时它们会把 $[l, i - 1]$ 这部分剩下的全部消掉。

  这样我们就不会在同一个栈（左边）剩东西，从而实现了 $f$ 的转移。

  为什么 $i$ 一定是最后消除的呢？理由同第一种情况。

  读者不妨可以模拟一下上图的具体过程。

  前提

  首先得保证存在这么一个 $i$，也就是存在 $i$ 使得 $p _ i > r$，即 $lx _ {l, r} \le r$。

  其次必须满足两个条件之一：

  1. $[l, i - 1]$ 与前面的 $[1, l - 1]$ 无关，即 $xl _ {l, i - 1} = l$（也可 $xl _ {l, i} = l$）；

  2. 不存在 $(j, k)$（$l \le j < i < k \le r$）满足 $p _ j < p _ k <l$， 也就是不存在 $p _ k$（$i < k \le r$）满足 $xl _ {l, i - 1} < p _ k < l$，即 $ly _ {l, i - 1} > r$（也可 $ly _ {l, i} > r$）。

  这里简要说明一下第二个条件。

  如果存在 $(j, k)$ 满足 $p _ j < p _ k < l$，根据性质，$p _ j, p _ k$ 在同一个栈中且 $p _ k$ 在 $p _ j$ 上面，这样 $j$ 就无法和 $p _ j$ 消去（$p _ j$ 被 $p _ k$ 卡住了）。

  总而言之就是要满足 $[l, i - 1]$ 的「有用的数」都在同一个栈的最顶部。

  而区间 $[l, r]$ 本身就满足「有用的数」在同一个栈的最顶部，所以可能造成干扰的是 $[i + 1, r]$ 这一部分，而不用考虑后面的部分。

  转移

  放入 $i$ 一定是合法的。所以只需判 $g _ {l, i - 1}$ 和 $f _ {i + 1, r}$ 的合法性即可。

  这时 $pf$ 数组不需记录信息，具体见「查找每个数放入的栈」。

  if (lx[l][r] <= r) // 第二种情况
  {
      now = lx[l][r];
      if (xl[now] == l || r < ly[now])
      {
          f[l][r] = g[l][now - 1] & f[now + 1][r];
      }
  }
  

• 第三种：$both \leftarrow f + f + both$

  概念

  

  如上图，这种情况当前区间不会产生剩余。于是我们选择 $p _ i > i$ 的 $i$。

  然后把区间分成 $[l, i - 1]$、$i$、$[i + 1, p _ i - 1]$、$p _ i$ 和 $[p _ i + 1, r]$ 五段。

  对于 $[l, i - 1]$ 这段，把它们放入另一个栈（右边）。

  对于 $i$，把它放入同一个栈（左边），这时它不会产生任何消除。

  对于 $[i + 1, p _ i - 1]$ 这段，把它们放入另一个栈（这时是左边），这时它们会把 $[l, i - 1]$ 这部分剩下的全部消掉。

  为什么这时候另一个栈是左边呢？因为左边的栈已经被 $i$ 堵住了，相当于是空栈（没用），但右边的栈很可能是「有用的栈」。

  对于 $p _ i$，把它放入另一个栈（右边），它已经和 $i$ 配好对，等待 $i$ 上面的数被消除即可。

  对于 $[p _ i + 1, r]$ 这段，把它们全部消掉，这时它们会把 $[i + 1, p _ i - 1]$ 这部分剩下的全部消掉。

  最后消掉 $i$ 和 $p _ i$。这样我们就不会剩东西，从而实现了 $both$ 的转移。

  很显然，$i$ 和 $p _ i$ 是最后消去的。

  读者不妨可以模拟一下上图的具体过程。

  前提

  首先要保证没有剩余，即 $lx _ {l, r} > r$。

  然后枚举 $i$ 的时候，要保证 $[i + 1, r]$ 与前面的 $[1, l - 1]$ 无关（否则就会被 $i$ 堵住），即 $ry _ {l, r} \le i$（也可 $ry _ {l, r} < i$）。

  还有要保证 $[p _ i + 1, r]$ 与 $[l, i - 1]$ 无关（否则就会被 $p _ i$ 堵住），即 $yr _ {l, i - 1} < p _ i$（也可 $yr _ {l, i - 1} \le p _ i$）。

  转移

  放入 $i, p _ i$ 和消除 $i, p _ i$ 一定是合法的。

  所以只需判 $f _ {l, i - 1}$、$f _ {i + 1, p _ i - 1}$ 和 $both _ {p _ i + 1, r}$ 的合法性即可。

  这时 $pboth$ 数组需要记录 $i$，具体见「查找每个数放入的栈」。

  if (lx[l][r] > r) // 第三种情况
  {
      for (int i = l, yr = l; i <= r; i ++)
      {
          if (p[i] < yr) continue;
          if (ry < i)
          {
              tmp = f[l][i - 1] & f[i + 1][p[i] - 1] & both[p[i] + 1][r];
              if (both[l][r] = tmp) {pboth[l][r] = i; goto skip;}
          }
          yr = p[i];
      }
      skip:;
  }
  

• 第四种：$both \leftarrow g + f + both$

  概念

  

  如上图，这种情况当前区间不会产生剩余。于是我们选择 $p _ i > i$ 的 $i$。

  然后把区间分成 $[l, i - 1]$、$i$、$[i + 1, p _ i - 1]$、$p _ i$ 和 $[p _ i + 1, r]$ 五段。

  对于 $[l, i - 1]$ 这段，把它们放入同一个栈（左边）。

  对于 $i$，把它放入另一个栈（右边），这时它不会产生任何消除。

  对于 $[i + 1, p _ i - 1]$ 这段，把它们放入另一个栈（右边），这时它们会把 $[l, i - 1]$ 这部分剩下的全部消掉。

  对于 $p _ i$，把它放入同一个栈（左边），它已经和 $i$ 配好对，等待 $i$ 上面的数被消除即可。

  对于 $[p _ i + 1, r]$ 这段，把它们全部消掉，这时它们会把 $[i + 1, p _ i - 1]$ 这部分剩下的全部消掉。

  最后消掉 $i$ 和 $p _ i$。这样我们就不会剩东西，从而实现了 $both$ 的转移。

  很显然，$i$ 和 $p _ i$ 是最后消去的。

  读者不妨可以模拟一下上图的具体过程。

  前提

  首先要保证没有剩余，即 $lx _ {l, r} > r$。

  其次枚举 $i$ 的时候，类似第二种情况，必须满足两个条件之一：

  1. $[l, i - 1]$ 与前面的 $[1, l - 1]$ 无关，即 $xl _ {l, i - 1} = l$（也可 $xl _ {l, i} = l$）；

  2. 不存在 $(j, k)$（$l \le j < i < k \le r$）满足 $p _ j < p _ k <l$， 也就是不存在 $p _ k$（$i < k \le r$）满足 $xl _ {l, i - 1} < p _ k < l$，即 $ly _ {l, i - 1} > r$（也可 $ly _ {l, i} > r$）。

  理由同第二种情况。

  然后要保证 $[p _ i + 1, r]$ 与前面的 $[1, l - 1]$ 无关（否则就会被 $p _ i$ 堵住），即 $ry _ {l, r} \le p _ i$（也可 $ry _ {l, r} < p _ i$）。

  还有要保证 $[p _ i + 1, r]$ 与 $[l, i - 1]$ 无关（否则就会被 $p _ i$ 堵住），即 $yr _ {l, i - 1} < p _ i$（也可 $yr _ {l, i - 1} \le p _ i$）。

  转移

  放入 $i, p _ i$ 和消除 $i, p _ i$ 一定是合法的。

  所以只需判 $g _ {l, i - 1}$、$f _ {i + 1, p _ i - 1}$ 和 $both _ {p _ i + 1, r}$ 的合法性即可。

  这时 $pboth$ 数组需要记录 $p _ i$，具体见「查找每个数放入的栈」。

  if (lx[l][r] > r) // 第四种情况
  {
      for (int i = l, yr = l; i <= r; i ++)
      {
          if (p[i] < yr) continue;
          if ((xl[i] == l || r < ly[i]) && ry < p[i])
          {
              tmp = g[l][i - 1] & f[i + 1][p[i] - 1] & both[p[i] + 1][r];
              if (both[l][r] = tmp) {pboth[l][r] = p[i]; goto skip;}
          }
          yr = p[i];
      }
      skip:;
  }
  

• 第五种：$both \leftarrow g + both$

  概念

  

  如上图，我们选择 $p _ i$ 最小的 $i$ 即 $p _ {xl _ {l, r}}$，然后把这个序列分成 $[l, i - 1]$、$i$ 和 $[i + 1, r]$ 三段。

  对于 $[l, i - 1]$ 这段，把它们放进同一个栈（左边）。

  对于 $i$，把它放进另一个栈（右边），这时它不会产生任何消除。

  对于 $[i + 1, r]$，把它们全部消去，这时它们会把 $[l, i - 1]$ 这部分剩下的全部消掉。

  这样我们就不会剩东西，从而实现了 $both$ 的转移。

  很显然，$i$ 是最后消去的。那为什么一定是 $i$ 呢？

  因为根据性质 $p _ i < p _ j < l$ 的 $j$ 肯定比它先消去（否则就堵住了），对于 $p _ j \ge l$ 的 $j$ 肯定存在一种方式让 $j, p _ j$ 先消去。

  当然也可以不选择那种方式，但是这段区间就可以拆成两个 $both$ 的区间相加了。

  读者不妨可以模拟一下上图的具体过程。

  前提

  首先要保证没有剩余，即 $lx _ {l, r} > r$。

  其次要保证要存在这个 $i$，也就是存在 $p _ i < l$ 的 $i$，即 $xl _ {l, r} < l$（其实也可以判 $ry _ {l, r} \ge l$，上文的 $lx$ 同样可以换成判 $yr$）。

  然后类似第二种情况，必须满足两个条件之一：

  1. $[l, i - 1]$ 与前面的 $[1, l - 1]$ 无关，即 $xl _ {l, i - 1} = l$；

  2. 不存在 $(j, k)$（$l \le j < i < k \le r$）满足 $p _ j < p _ k <l$， 也就是不存在 $p _ k$（$i < k \le r$）满足 $xl _ {l, i - 1} < p _ k < l$，即 $ly _ {l, i - 1} > r$。

  理由同第二种情况。

  转移

  放入 $i$ 一定是合法的。所以只需判 $g _ {l, i - 1}$ 和 $both _ {i + 1, r}$ 的合法性即可。

  这时 $pboth$ 数组需要记录 $-i$，具体见「查找每个数放入的栈」。

  if (lx[l][r] > r) // 第五种情况
  {
      if (xl[r] < l)
      {
          now = p[xl[r]];
          if (xl[now - 1] == l || r < ly[now - 1])
          {
              tmp = g[l][now - 1] & both[now + 1][r];
              if (both[l][r] = tmp) pboth[l][r] = -now;
          }
      }
  }
  

容易发现只有这几种情况，分别转移即可。

对于第二、四、五种情况，其实如果预处理 $ly _ {i, i - 1}$，那么前提两个条件中的第一个条件可以略去。

因为当 $xl _ {l, i} = l$ 时，$ly _ {l, i}$ 一定等于无穷大，也就是满足 $ly _ {l, i} > r$。只是作者太懒了代码不想改 qwq。

目标状态

如果 $both _ {1, n} = 1$，则有解（输出 Cleared.）；否则无解（输出 No solution）。

关于 $both$ 数组的补充说明

很显然，当 $[l, r]$ 内没有剩余即 $lx _ {l, r} > r$ 时，$both$ 数组取 $f$ 和 $g$ 任意一个都行（相当于把空集堆在任意一个栈）。

因此我们转移时可以把 $both$ 都换成 $f$，转移后再把 $g \leftarrow f$ 就可以了。

记录上一个状态的数组 $pboth$ 也可换成 $pf$，转移后再把 $pg \leftarrow pf$ 即可。

关于性质的粗略证明

证明：

考虑用数学归纳法。命题对于 $[1, n]$ 显然成立（都没有「有用的数」）。

设命题对于 $[l, r]$ 成立，接下来证明命题对于由它分割的一个子区间 $[l ^ \prime, r ^ \prime]$ 依然成立。

对于第一种情况（$g = f + f$），$[l, r]$ 的「有用的数」都是 $[l, i - 1]$ 的，命题对于 $[l, i - 1]$ 显然成立；

而前提保证 $[i + 1, r]$ 的「有用的数」都在 $[l, i - 1]$ 中被堆在了另一个栈且只剩下「有用的数」，命题也成立。

对于第二种情况（$f = g + f$），根据我们在第二种情况时的讨论，命题对于 $[l, i - 1]$ 显然成立；

而 $[i + 1, r]$ 的「有用的数」要么就在之前「有用的栈」的最顶部，要么就在 $[l, i - 1]$ 剩下的当中，命题也成立。

因为前提保证了 $[l, i - 1]$ 只会剩下「有用的数」，所以「有用的数」仍在同一个栈的最顶部。

对于第三种情况（$both = f + f + both$），同第一种情况，命题对于 $[l, i - 1]$ 显然成立；

命题对于 $[i + 1, p _ i - 1]$ 同样成立，理由同第一种情况；

前提保证了 $[1, l - 1]$ 和 $[l, i - 1]$ 部分都没有 $[p _ i + 1, r]$ 的「有用的数」，所以「有用的数」只会在 $[i + 1, p _ i - 1]$ 当中，命题也成立。

因为前提保证了 $[p _ i + 1, r]$ 只会剩下「有用的数」，所以「有用的数」仍在同一个栈的最顶部。

对于第四种情况（$both = g + f + both$），同第二种情况，命题对于 $[l, i - 1]$ 显然成立；

命题对于 $[i + 1, p _ i - 1]$ 同样成立，理由同第二种情况；

对于 $[p _ i + 1, r]$ 这部分同第三种情况，命题也成立。

对于第五种情况（$both = g + both$），同第二种情况，命题对于 $[l, i - 1]$ 显然成立；

命题对于 $[i + 1, r]$ 同样成立，理由同第二种情况。

证毕。

Part 3：求具体方案

首先容易发现 $op = \frac 3 2 n$，因为每个数都被进行了一次加入操作，两个数一组被进行了一次消除操作。

查找每个数放入的栈

设 $gt _ i$ 为第 $i$ 个数应该放入的栈。$gt _ i = 0$ 表示放入栈 $1$，$gt _ i = 1$ 表示放入栈 $2$。

记 $pre _ {l, r, w} = \begin {cases} pf _ {l, r} & (w = 1) \\ pg _ {l, r} & (w = 0) \end {cases}$，可以有效简化步骤。

特别提醒：根据「关于 $both$ 数组的补充说明」，此时 $both$ 数组已并入 $f$ 和 $g$ 中， $pboth$ 数组已并入 $pf$ 和 $pg$ 中。

考虑递归查找。需要传入四个参数：$l, r, w, d$，表示当前递归到区间 $[l, r]$，是第 $w$ 种转移方式，同一个栈为栈 $d$。

这里 $w = 1$ 表示转移方式 $f$，$w = 0$ 表示转移方式 $g$；$d = 0$ 表示栈 $1$，$d = 1$ 表示栈 $2$。

查找的入口为区间 $[1, n]$，我们钦定 $w = d = 0$。

如果当前递归查找的区间为 $[l, r]$，是第 $w$ 种转移方式，同一个栈为栈 $d + 1$，分几种情况：

• 第一、二种情况

  判定

  如果满足 $lx _ {l, r} \le r$，那么说明是第一、二种情况。

  查找分界点放入的栈

  不管是第一种情况还是第二种情况，分界点都是 $lx _ {l, r}$。

  然而还要考虑 $w$ 的影响。发现 $f$ 的分界点被放入另一个栈，而 $g$ 的分界点被放入同一个栈。也就是说 $w = 1$ 时要反过来。

  总结规律可以得出 $gt _ {lx _ {l, r}} = w ~ \mathrm {xor} ~ d$。

  递归

  第一种情况是 $g = f + f$，第二种情况是 $f = g + f$。

  发现两种情况的共同点是都只有两个子区间，其中左边子区间的转移方式与当前区间相反，且右边子区间转移方式为 $f$。

  而左边子区间同一个栈与当前区间相同，右边子区间同一个栈如果 $w = 0$ 那么还要反过来。

  所以分别递归 $(l, lx _ {l, r} - 1, !w, d)$ 和 $(lx _ {l, r} + 1, r, 1, !w ~ \mathrm {xor} ~ d)$。

• 第三种情况

  判定

  如果满足 $lx _ {l, r} > r$ 且 $pre _ {l, r, w} > 0$ 且 $pre _ {l, r, w} < p _ {pre _ {l, r, w}}$，那么说明是第三种情况。

  查找分界点放入的栈

  靠左的分界点 $pre _ {l, r, w}$ 会被放入同一个栈，靠右的分界点 $p _ {pre _ {l, r, w}}$ 会被放入另一个栈。

  令 $gt _ {pre _ {l, r, w}} = d$，$gt _ {p _ {pre _ {l, r, w}}} = ~ !d$。

  递归

  三个子区间转移方式都为 $f$（这里我们把右边子区间的转移方式钦定为 $f$）。

  左边子区间同一个栈与当前区间相同，中间子区间同一个栈与当前区间相反，右边子区间同一个栈与当前区间相同。

  所以分别递归 $(l, pre _ {l, r, w} - 1, 1, d)$、$(pre _ {l, r, w} + 1, p _ {pre _ {l, r, w}} - 1, 1, !d)$ 和 $(p _ {pre _ {l, r, w}} + 1, r, 1, d)$。

• 第四种情况

  判定

  如果满足 $lx _ {l, r} > r$ 且 $pre _ {l, r, w} > 0$ 且 $pre _ {l, r, w} > p _ {pre _ {l, r, w}}$，那么说明是第四种情况。

  查找分界点放入的栈

  靠左的分界点 $p _ {pre _ {l, r, w}}$ 会被放入另一个栈，靠右的分界点 $pre _ {l, r, w}$ 会被放入同一个栈。

  令 $gt _ {p _ {pre _ {l, r, w}}} = ~ !d$，$gt _ {pre _ {l, r, w}} = d$。

  递归

  左边子区间转移方式为 $g$，其它子区间转移方式都为 $f$（这里我们把右边子区间的转移方式钦定为 $f$）。

  左边子区间同一个栈与当前区间相同，中间子区间同一个栈与当前区间相同，右边子区间同一个栈与当前区间相反。

  所以分别递归 $(l, p _ {pre _ {l, r, w}} - 1, 0, d)$、$(p _ {pre _ {l, r, w}} + 1, p _ {l, r, w} - 1, 1, d)$ 和 $(p _ {l, r, w} + 1, r, 1, !d)$。

• 第五种情况

  判定

  如果满足 $lx _ {l, r} > r$ 且 $pre _ {l, r, w} < 0$，那么说明是第五种情况。

  查找分界点放入的栈

  分界点 $-pre _ {l, r, w}$ 会被放入另一个栈。

  令 $gt _ {-pre _ {l, r, w}} = ~ !d$。

  递归

  左边子区间转移方式为 $g$，右边子区间转移方式我们钦定为 $f$。

  左边子区间和右边子区间同一个栈都与当前区间相同。

  所以分别递归 $(l, -pre _ {l, r, w} - 1, 0, d)$ 和 $(-pre _ {l, r, w} + 1, 1, d)$。

模拟具体操作

得出 $gt$ 数组后，我们从前往后遍历每一个数。设当前遍历到位置 $i$，数为 $A _ i$。

首先如果 $gt _ i = 0$，那么输出 1；否则输出 2。然后把 $A _ i$ 压入对应的栈中。

在栈顶数字相同的情况下，一直输出 0 并弹出两边栈顶。

---

于是我们就可以愉快地搞定一道黑题啦。下面附上 AC 代码：

AC Code

#include <cstdio>
#include <cstring>
#define inf 0x3f3f3f3f
#define N 1505
#define min(x,y) ((x)<(y)?(x):(y))
using namespace std;

int n, a[N], l[N], p[N], gt[N], pf[N][N], pg[N][N];
int lx[N][N], xl[N], ly[N], tr[N];
int top[2], st[2][N]; // 数组模拟栈
bool tmp, f[N][N], g[N][N];

int &pre (int i, int j, bool k) // 合并两个数组为一个函数
{
    return k ? pf[i][j] : pg[i][j];
}

// 这里的树状数组写法有些不同，实现的是单点修改，区间（后缀）询问

void modify (int p, int c) // 树状数组加入元素
{
    for (; p; p &= p - 1) tr[p] = min (tr[p], c);
    return ;
}

int ask (int p) // 树状数组询问
{
    int res = inf;
    for (; p <= n; p += p & -p) res = min (res, tr[p]);
    return res;
}

void dfs (int l, int r, bool w, bool d) // dfs 求具体方案
{
    if (l > r) return ;
    if (lx[l][r] <= r)
    {
        gt[lx[l][r]] = w ^ d;
        dfs (l, lx[l][r] - 1, !w, d);
        dfs (lx[l][r] + 1, r, 1, !w ^ d);
    }
    else
    {
        if (pre (l, r, w) > 0)
        {
            gt[pre (l, r, w)] = d;
            gt[p[pre (l, r, w)]] = !d;
            if (pre (l, r, w) < p[pre (l, r, w)])
            {
                dfs (l, pre (l, r, w) - 1, 1, d);
                dfs (pre (l, r, w) + 1, p[pre (l, r, w)] - 1, 1, !d);
                dfs (p[pre (l, r, w)] + 1, r, 1, d);
            }
            else
            {
                dfs (l, p[pre (l, r, w)] - 1, 0, d);
                dfs (p[pre (l, r, w)] + 1, pre (l, r, w) - 1, 1, d);
                dfs (pre (l, r, w) + 1, r, 1, !d);
            }
        }
        else
        {
            gt[-pre (l, r, w)] = !d;
            dfs (l, -pre (l, r, w) - 1, 0, d);
            dfs (-pre (l, r, w) + 1, r, 1, d);
        }
    }
    return ;
}

int main ()
{
    scanf ("%d", &n), f[1][0] = g[1][0] = 1; // 初始化
    for (int i = 1; i <= n; i ++)
    {
        scanf ("%d", &a[i]);
        if (l[a[i]]) p[l[a[i]]] = i, p[i] = l[a[i]]; // 预处理
        l[a[i]] = i, f[i + 1][i] = g[i + 1][i] = 1; // 初始化
    }
    for (int r = 1; r <= n; r ++)
    {
        lx[r + 1][r] = r + 1; // 初始化
        for (int l = r; l; l --) // 预处理
        {
            lx[l][r] = lx[l + 1][r];
            if (p[l] > r) lx[l][r] = l;
        }
    }
    for (int l = n, ry = 0; l; l --, ry = 0)
    {
        xl[l - 1] = l, memset (tr, 0x3f, sizeof tr); // 初始化
        for (int r = l; r <= n; r ++) // 预处理
        {
            xl[r] = min (xl[r - 1], p[r]);
        }
        for (int r = n; r >= l; r --) // 预处理
        {
            ly[r] = ask (xl[r]);
            if (p[r] < l) modify (p[r], r);
        }
        for (int r = l, now; r <= n; r ++) // 区间 dp
        {
            if (p[r] < l) ry = r; // 顺便预处理
            if (lx[l][r] <= r)
            {
                now = lx[l][r];
                if (ry < now) g[l][r] = f[l][now - 1] & f[now + 1][r]; // 第一种情况
                if (xl[now] == l || r < ly[now]) // 第二种情况
                {
                    f[l][r] = g[l][now - 1] & f[now + 1][r];
                }
            }
            else
            {
                for (int i = l, yr = l; i <= r; i ++)
                {
                    if (p[i] < yr) continue;
                    if (ry < i) // 第三种情况
                    {
                        tmp = f[l][i - 1] & f[i + 1][p[i] - 1] & f[p[i] + 1][r];
                        if (f[l][r] = tmp) {pf[l][r] = i; goto skip;}
                    }
                    if ((xl[i] == l || r < ly[i]) && ry < p[i]) // 第四种情况
                    {
                        tmp = g[l][i - 1] & f[i + 1][p[i] - 1] & f[p[i] + 1][r];
                        if (f[l][r] = tmp) {pf[l][r] = p[i]; goto skip;}
                    }
                    yr = p[i]; // 顺便预处理
                }
                if (xl[r] < l)
                {
                    now = p[xl[r]];
                    if (xl[now - 1] == l || r < ly[now - 1]) // 第五种情况
                    {
                        tmp = g[l][now - 1] & f[now + 1][r];
                        if (f[l][r] = tmp) pf[l][r] = -now;
                    }
                }
                skip:; g[l][r] = f[l][r], pg[l][r] = pf[l][r]; // 关于 Both 的处理
            }
        }
    }
    puts (f[1][n] ? "Cleared." : "No solution.");
    if (!f[1][n]) return 0;
    printf ("%d\n", n / 2 * 3), dfs (1, n, 0, 0);
    for (int i = 1; i <= n; i ++) // 模拟
    {
        putchar ('1' + gt[i]), st[gt[i]][++ top[gt[i]]] = a[i];
        while (top[0] && top[1] && st[0][top[0]] == st[1][top[1]])
        {
            putchar ('0'), top[0] --, top[1] --;
        }
    }
    return 0;
}

题解若有问题欢迎在评论区反馈。