自动搬运

查看原文

来自洛谷，原作者为

	__K2FeO4 Purple, Indigo, Lavender, Lilac, Grape, Ningyezi, Amethyst, Hyacinth, Mauve, Blurple

搬运于2025-08-24 22:47:20，当前版本为作者最后更新于2023-05-13 11:51:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

我花费了一周完成这道题。

这道题需要揣摩各种国际象棋棋子的性质。

在我的代码中，各个棋子有自己的编号。

编号	字母	英文	中文
$1$	P	pawn	兵
$2$	R	rook	车
$3$	N	knight	马
$4$	B	bishop	象
$5$	Q	queen	后
$6$	K	king	王

其实编号可以随便给。

scanf("%s",s+1);
scanf("%d %d %d %d",&a,&b,&c,&d);
for(int i=1;i<=6;i++){
	switch(s[i]){
		case 'P':v[1]=1;break;
		case 'R':v[2]=1;break;
		case 'N':v[3]=1;break;
		case 'B':v[4]=1;break;
		case 'Q':v[5]=1;break;
		case 'K':v[6]=1;break;
	}
}

Queen

皇后的功能繁多，拥有了除了马以外的所有功能。

由于其横、竖、斜通过的距离不限，如果两点在同一横、竖、斜线上，那么她一步就能到达。若 $a\ne b,c\ne d$，她可以从 $(a,b)$ 走到 $(c,b)$，再到 $(c,d)$。或者其他的一次性从与终点非共横竖斜到共横竖斜。于是最多两次就能到达。

若超级棋子中有马的功能，则先判是否能用马一次性到达。然而绝对不会有先跳马再走后比走两次后更优的情况。因此若不能一次性到达，则不用再在这个基础上判定后了。

if(v[5]){//q
	int ans=2;
	if(v[3]){//n
		for(int i=0;i<8;i++)
		if(a+dn[i][0]==c&&b+dn[i][1]==d){
			ans=1;break;
		}
	}
	if(a==c||b==d||a-c==b-d||a-c==d-b)ans=1;
	printf("%d\n",ans);
}

Rook

车和皇后类似，去掉斜向功能没有太大的障碍，仍然可以从 $(a,b)$ 走到 $(c,b)$，再到 $(c,d)$。

马照样要特判，除此之外，王也要特判。说白了，就是四个斜角要特判一下。

else if(v[2]){//r
	int ans=2;
	if(v[3]){//n
		for(int i=0;i<8;i++)
		if(a+dn[i][0]==c&&b+dn[i][1]==d){
			ans=1;break;
		}
	}
	if(v[6]){//k
		for(int i=1;i<8;i+=2)
		if(a+dk[i][0]==c&&b+dk[i][1]==d){
			ans=1;break;
		}
	}
	if(v[4]&&(a-c==b-d||a-c==d-b))ans=1;//b
	if(a==c||b==d)ans=1;
	printf("%d\n",ans);
}

Bishop

象就不一样了。它只能斜着走，在国际象棋棋盘中，一个象只能在同种颜色的格子中行走。表现在这道题中，$x+y$ 的奇偶性保持不变。

因此，若超级棋子功能只有象，且 $a+b$ 与 $c+d$ 的奇偶性不一致，则无解，输出 $-1$。否则，奇偶性一致，则与后、车类似，最多两步到达。

若功能不止是象，则剩下的功能马、王（这里指横竖）、兵，每走一步，可以改变所在格子的颜色。这一步之后，再判象要几次。特别注意不要漏掉马王兵的一步到达。

else if(v[4]){//b
	if((a^b^c^d)&1){//odd
		int ans=3;
		bool fg=true;
		if(v[3]){//n
			fg=false;
			for(int i=0;i<8;i++){
				int na=a+dn[i][0],nb=b+dn[i][1];
				if(na==c&&nb==d){
					ans=1;break;
				}
				else if(na-c==nb-d||na-c==d-nb){
					ans=min(ans,2);
				}
			}
		}
		if(v[6]){//k
			fg=false;
			for(int i=0;i<8;i+=2){
				int na=a+dk[i][0],nb=b+dk[i][1];
				if(na==c&&nb==d){
					ans=1;break;
				}
				else if(na-c==nb-d||na-c==d-nb){
					ans=min(ans,2);
				}
			}
		}
		if(v[1]){//p
			fg=false;
			if(a+1==c&&b==d)ans=1;
			else if(a+1-c==b-d||a+1-c==d-b)ans=min(ans,2);
		}
		if(fg)puts("-1");//no
		else printf("%d\n",ans);//yes
	}
	else{//even
		if(a-c==b-d||a-c==d-b)puts("1");
		else puts("2");
	}
}

Knight

马是这道题的重点。

有人说像这道题一样搜一遍就行了。然而，数据太大，喜提 TLE/MLE。

缩小数据，打个表试试？

20 20 20 1
11 10 11 10 11 10 11 10 11 10 11 10 11 12 11 12 13 12 13 14
10 9  10 9  10 9  10 9  10 9  10 11 10 11 12 11 12 13 12 13
9  10 9  10 9  10 9  10 9  10 9  10 11 10 11 12 11 12 13 12
8  9  8  9  8  9  8  9  8  9  10 9  10 11 10 11 12 11 12 13
9  8  9  8  9  8  9  8  9  8  9  10 9  10 11 10 11 12 11 12
8  7  8  7  8  7  8  7  8  9  8  9  10 9  10 11 10 11 12 11
7  8  7  8  7  8  7  8  7  8  9  8  9  10 9  10 11 10 11 12
6  7  6  7  6  7  6  7  8  7  8  9  8  9  10 9  10 11 10 11
7  6  7  6  7  6  7  6  7  8  7  8  9  8  9  10 9  10 11 10
6  5  6  5  6  5  6  7  6  7  8  7  8  9  8  9  10 9  10 11
5  6  5  6  5  6  5  6  7  6  7  8  7  8  9  8  9  10 9  10
4  5  4  5  4  5  6  5  6  7  6  7  8  7  8  9  8  9  10 11
5  4  5  4  5  4  5  6  5  6  7  6  7  8  7  8  9  10 9  10
4  3  4  3  4  5  4  5  6  5  6  7  6  7  8  9  8  9  10 11
3  4  3  4  3  4  5  4  5  6  5  6  7  8  7  8  9  10 9  10
2  3  2  3  4  3  4  5  4  5  6  7  6  7  8  9  8  9  10 11
3  2  3  2  3  4  3  4  5  6  5  6  7  8  7  8  9  10 9  10
2  1  4  3  2  3  4  5  4  5  6  7  6  7  8  9  8  9  10 11
3  4  1  2  3  4  3  4  5  6  5  6  7  8  7  8  9  10 9  10
0  3  2  3  2  3  4  5  4  5  6  7  6  7  8  9  8  9  10 11

其中我们要把最靠近左下角的 $4$ 改为 $2$，因为左边和下面本身是可以跳出去的。

我用 Python 编写了可视化程序，效果在此（那个 $4$ 已改为 $2$，输入数据已修改）

我们发现了两条明显的“山脊”。然后，进行分层。

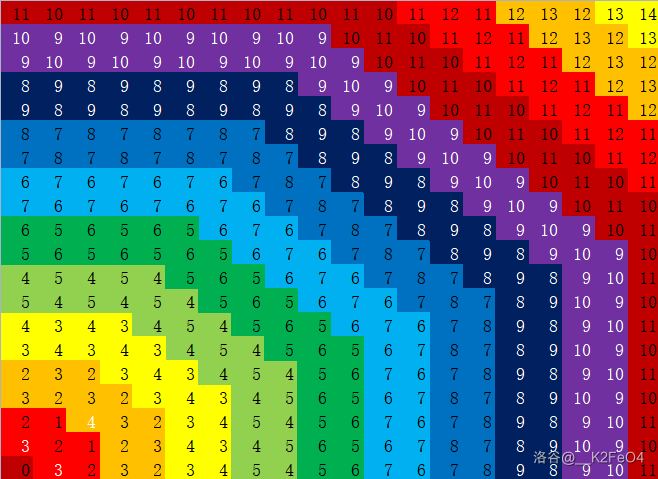
左下角三个特例已用白色标出，其余白色是为了能看清楚。

我们以左下角原始坐标为第 $0$ 层，则大红色、橙色、黄色依次为 $1,2,3$ 层。右上角出现循环是因为颜色不够用了。

不难发现，第 $i$ 层与原始坐标的切比雪夫距离不超过 $2i$，曼哈顿距离不超过 $3i$。

于是我们可以写出公式：

$gr=\max\left\{\left\lceil\dfrac{x}{2}\right\rceil,\left\lceil\dfrac{y}{2}\right\rceil,\left\lceil\dfrac{x+y}{3}\right\rceil\right\}$

我们定义 $x+y$ 为奇数的格叫白格，为偶数叫黑格。因为国际象棋棋盘中左下角的格是黑格。

并且，在奇数层中，黑格比白格步数多一；在偶数层中，白格比黑格步数多一。

于是在程序中异或就能算出来。

int knight(int x,int y){
	int ans;
	if((x==0&&y==1)||(x==1&&y==0))ans=3;
	else if(x==2&&y==2)ans=4;
	else{
		int gr=max(max((x+1)/2,(y+1)/2),(x+y+2)/3);
		ans=((gr^x^y)&1)+gr;
	}
	return ans;
}

那么有兵和王怎么办？我们注意到，在非特殊的三格中，有些格左下角的步数比它少 $2$。因此，在马的一系列操作后，王可以一步到达。

兵和王，走两步及以上一定不优。因为它们可以转换成最多一次兵、王与另外几次马的情形。兵唯一的作用是到 $(2,2)$ 格走一步，且背道而驰也是不优的。至于王在这种情形中，就能向竖直方向靠近一步。

既然刚才的函数内部复杂度是 $O(1)$ 的，在兵与王能到达的格子进行枚举也不成问题。

else if(v[3]){//n
	int ans=knight(abs(a-c),abs(b-d));
	if(v[1])ans=min(ans,1+knight(abs(a-c+1),abs(b-d)));
	if(v[6]){
		for(int i=0;i<8;i++)
		ans=min(ans,1+knight(abs(a-c+dk[i][0]),abs(b-d+dk[i][1])));
	}
	printf("%d\n",ans);
}

King

这就很简单了。先走斜线，等到与终点横纵任一坐标一致时，改横竖方向。本质上是切比雪夫距离。

else if(v[6])printf("%d\n",max(abs(a-c),abs(b-d)));//k

Pawn

这更简单了。只要判起点是否与终点在同一纵轴上且在终点下面即可。

else if(a<c&&b==d)printf("%d\n",c-a);//p
else puts("-1");

---

最后，上完整代码！为了反作弊我改了一个地方。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=444422;
const int dn[8][2]={1,2,2,1,-1,2,2,-1,1,-2,-2,1,-1,-2,-2,-1};
const int dk[8][2]={1,0,1,1,0,1,-1,1,-1,0,-1,-1,0,-1,1,-1};
int q,a,b,c,d;
char s[8];
bool v[8];//1=Pawn,2=Rook,3=kNight,4=Bishop,5=Queen,6=King
int knight(int x,int y){
	int ans;
	if((x==0&&y==1)||(x==1&&y==0))ans=3;
	else if(x==2&&y==2)ans=4;
	else{
		int gr=max(max((x+1)/2,(y+1)/2),(x+y+2)/3);
		ans=((gr^x^y)&1)+gr;
	}
	return ans;
}
int mian(){
	scanf("%d",&q);
	while(q--){
		memset(s,0,sizeof(s));
		memset(v,0,sizeof(v));
		scanf("%s",s+1);
		scanf("%d %d %d %d",&a,&b,&c,&d);
		for(int i=1;i<=6;i++){
			switch(s[i]){
				case 'P':v[1]=1;break;
				case 'R':v[2]=1;break;
				case 'N':v[3]=1;break;
				case 'B':v[4]=1;break;
				case 'Q':v[5]=1;break;
				case 'K':v[6]=1;break;
			}
		}
		//for(int i=1;i<=6;i++)printf("%d",v[i]);
		if(v[5]){//q
			int ans=2;
			if(v[3]){//n
				for(int i=0;i<8;i++)
				if(a+dn[i][0]==c&&b+dn[i][1]==d){
					ans=1;break;
				}
			}
			if(a==c||b==d||a-c==b-d||a-c==d-b)ans=1;
			printf("%d\n",ans);
		}
		else if(v[2]){//r
			int ans=2;
			if(v[3]){//n
				for(int i=0;i<8;i++)
				if(a+dn[i][0]==c&&b+dn[i][1]==d){
					ans=1;break;
				}
			}
			if(v[6]){//k
				for(int i=1;i<8;i+=2)
				if(a+dk[i][0]==c&&b+dk[i][1]==d){
					ans=1;break;
				}
			}
			if(v[4]&&(a-c==b-d||a-c==d-b))ans=1;//b
			if(a==c||b==d)ans=1;
			printf("%d\n",ans);
		}
		else if(v[4]){//b
			if((a^b^c^d)&1){//odd
				int ans=3;
				bool fg=true;
				if(v[3]){//n
					fg=false;
					for(int i=0;i<8;i++){
						int na=a+dn[i][0],nb=b+dn[i][1];
						if(na==c&&nb==d){
							ans=1;break;
						}
						else if(na-c==nb-d||na-c==d-nb){
							ans=min(ans,2);
						}
					}
				}
				if(v[6]){//k
					fg=false;
					for(int i=0;i<8;i+=2){
						int na=a+dk[i][0],nb=b+dk[i][1];
						if(na==c&&nb==d){
							ans=1;break;
						}
						else if(na-c==nb-d||na-c==d-nb){
							ans=min(ans,2);
						}
					}
				}
				if(v[1]){//p
					fg=false;
					if(a+1==c&&b==d)ans=1;
					else if(a+1-c==b-d||a+1-c==d-b)ans=min(ans,2);
				}
				if(fg)puts("-1");//no
				else printf("%d\n",ans);//yes
			}
			else{//even
				if(a-c==b-d||a-c==d-b)puts("1");
				else puts("2");
			}
		}
		else if(v[3]){//n
			//int x=abs(a-c),y=abs(b-d);
			int ans=knight(abs(a-c),abs(b-d));
			if(v[1])ans=min(ans,1+knight(abs(a-c+1),abs(b-d)));
			if(v[6]){
				for(int i=0;i<8;i++)
				ans=min(ans,1+knight(abs(a-c+dk[i][0]),abs(b-d+dk[i][1])));
			}//ans=min(min(min(ans,1+knight(x-1,y)),
			//1+min(knight(x,y-1),knight(x-1,y-1))),1+knight(x-1,y+1));
			printf("%d\n",ans);
		}
		else if(v[6])printf("%d\n",max(abs(a-c),abs(b-d)));//k
		else if(a<c&&b==d)printf("%d\n",c-a);//p
		else puts("-1");
	}
	
	return 0;
}

完结散花！