自动搬运

查看原文

来自洛谷，原作者为

	y_kx_b 清新题目今何在 ～ Lunatic Probrems Everywhere

搬运于2025-08-24 22:47:12，当前版本为作者最后更新于2023-02-03 17:59:53，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

呜呜，本来想友情在题面里提醒一下 B2（k=2 version）> C1 的，结果我不能修改团队题目/ng

$\textbf{Sub }{\sf1}\textbf:$ 以根节点为一端点的链。

因为只有一个叶子节点，所以答案为 $0$ （因为所有边都在根到叶子节点的路径内，两个边集均为空）。

$\textbf{Sub }{\sf6}\textbf:$ 链。

如果根节点不为链的端点，显然根节点答案为左右两条链的重量的最小值。非根节点转化为 $\text{Sub }{\sf1}$，答案为 $0$。

$\textbf{Sub }{\sf5}\textbf:$ $k=1$ 正解

一个简单 dfs 就结束了，这不需要讲吧（）。

好吧考虑到这题的位置还是讲讲吧，我们 dfs 这棵树，儿子就按照一个方向搜，当搜到叶子节点的时候统计这条链带来的贡献，最后所有贡献取最小值输出即可。

另外一个链式前向星的细节，读入顺序是从左往右，可前向星加边后遍历是反着的。这可能作为一个坑点，虽然这题没关系因为从左往右还是从右到左都一样。

代码中的 w1 代表链左边边集的边权和，w2 代表链上的边权和，(wsum - w2 - w1) 就是右边的边权和啦。

int wsum = 0/*读入完成后 wsum = 整棵树的边权总和*/, w1 = 0;
int ans = 0x7f7f7f7f;
void dfs(int u, int w2) {
	if(head[u] == -1) {
		ans = min(ans, abs((wsum - w2 - w1) - w1));
		return;//其实这里写不写都无所谓，因为叶子节点肯定进不了下面这个循环（）
	}
	for(int i = head[u]; ~i; i = ne[i]) {
		int &v = to[i];
		dfs(v, w2 + w[i]);
		w1 += w[i];
	}
}

$m_i\leqslant10^4$，所以不用开 long long。

$\textbf{Sub }{\sf4}\textbf:$ 菊花图。

容易发现问题可以转化为序列上的问题。

有一个长度为 $n-1$ 的序列 $m$，计算 $\min\limits_{k=1}^{n-1}{\left\vert\sum\limits_{i=1}^{k-1}m_i-\sum\limits_{i=k+1}^{n-1}m_i\right\vert}$。

因为 $m_i>0$，所以这个柿子（绝对值内部）肯定是单调的。所以预处理后直接二分就行。

后来发现非根节点没有儿子，答案一定为 $0$，因此只需要计算根节点的答案，直接 $O(n)$ 枚举 $k$ 这个 Sub 就做完了，很遗憾没有太对正解起到启发作用/kk

$\textbf{Sub }{\sf7}\textbf:$ $k=2$ 正解

其实就是上面这个 $\sout{O(\log n)\text{ Sub}{\sf4}}$。

我们发现，每当选择的叶子节点越来越靠右，右边的边权和减去左边的边权和一定越来越小（单调递减）。那么对于每个点的子树的询问，我们就可以直接二分，单次询问复杂度 $O(\log n)$。这里对于每个点都有询问，$q=n$，总复杂度为 $O(n\log n)$。

看个具体的例子吧。注意这里我们假设 $2$ 为根。

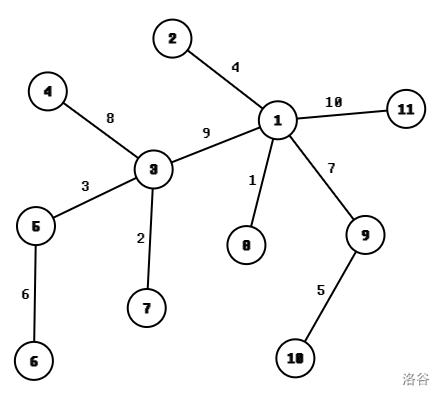
我们首先按照 $\text{Sub }{\sf5}$ 的 dfs 预处理出每个叶子节点相对根的的 w1 和 w2 以及每个点子树内包含的叶子节点的范围（即 dfs 序）。比如这里，w1[9]=9+8+3+6+2+1，w1[3]=0，w2[7]=4+9+2。那么我们就可以用前缀和思想，把相对于根节点的 w 变成相对于某个给出的根的 w，比如 $3$ 子树内的 $7$ 的 w1 = w1[7]-w1[3]=8+3+6，w2 同理。

然后就可以二分啦。

std 写的很丑，仅供思路参考用 qwq

代码中 ww1[i] 表示节点 $i$ 的 w1，w1[i] 表示第 $i$ 个叶子节点的 w1；w2同理。wsum 为一个点子树内所有的边权总和。

int k;
int to[N], ne[N], w[N], head[N], idx1 = 0;
void add(int u, int v, int W) {
	to[idx1] = v, w[idx1] = W, ne[idx1] = head[u], head[u] = idx1++;
}

int wsum[N], ww1[N], ww2[N];
int w1[N], w2[N], idx2 = 0;
pii dfn[N];//左闭右开
int W1 = 0;
void dfs0(int u, int W2) {
	dfn[u].x = idx2;
	ww1[u] = W1, ww2[u] = W2;//ww1必须前序遍历记录。
	if(head[u] == -1)
		w1[/*u*/idx2] = W1, w2[idx2++] = W2;
	for(int i = head[u]; ~i; i = ne[i]) {
		int &v = to[i];
		dfs0(v, W2 + w[i]);
		wsum[u] += w[i] + wsum[v], W1 += w[i];
	}
	dfn[u].y = idx2;
}
int f(int u, int x) {
	//     ( wsum   -        w2        -        w1        * 2);
	return (wsum[u] - (w2[x] - ww2[u]) - (w1[x] - ww1[u]) * 2);
}
bool major(int T = 1) {
	// memset(head, -1, sizeof head);// will TLE for T = 4e3
	int n = read();
	idx1 = idx2 = 0; W1 = 0;
	for(int i = 1; i <= n; i++) head[i] = -1, wsum[i] = 0;
	for(int i = 1; i <= n; i++) {
		int q = read();
        while(q--) {
			int v = read(), y = read();
			add(i, v, y);
		}
	}
	dfs0(1, 0);
	for(int u = 1; u <= n; u++) {
		int l = dfn[u].x, r = dfn[u].y - 1;
		while(l + 1 < r) {//五点七边二分法 yyds！
			int mid = l + r >> 1;
			if(f(u, mid) >= 0) l = mid; else r = mid;
		}
		// if(l == r) ans = abs(f(u, l)); else 
        // 本来要特判叶子节点，但是直接进入下面的语句也是对的（）。
		int ans = min(abs(f(u, l)), abs(f(u, r)));
		if(k == 2)
			printf("%d%c", ans, " \n"[u == n]);
		else //if(u == 1) 
			return printf("%d\n", ans);
	}
	return 0;
}

完结撒花！

彩蛋：题目中有一句白色的 $\sout{\text{不要问我为什么重量的字母是 }m\text。}$ ，不过好像梅友仁真正地问（）因为本来这场比赛就没给彩蛋供钱（

upd1 at 23.2.7：造数据时一直在想 $T$ 大了可能就放 $O(n^2)$ 过去了，结果忘了卡全局 memset（雾）。

upd2 at 23.4.28：唔，听说可以树形 dp？那是什么神仙做法，不懂。至少我尝试过然后没做出来/ng

upd3 at 24/12/06：原来之前一直把五点七边二分法（二分查找为什么总是写错？）的 up 主记成了 3b1b，磕头谢罪）