自动搬运

查看原文

来自洛谷，原作者为

	Jeefy 要记得生活中有个生，不要只是活着

搬运于2025-08-24 22:47:02，当前版本为作者最后更新于2023-06-02 14:06:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

[ROI 2018] Innophone

看了半天网上仅有的一篇题解……才堪堪写出来。

不过在LOJ上看提交，全是 KTT，看得我瑟瑟发抖~~（不会~~。

题意翻译

在平面上有一些点，你需要在这个平面上任意确定一个点（不要求是给定的点），定义其贡献为 横坐标 $\times$ 其右侧的点 $+$ 纵坐标 $\times$ 其左上方的点：

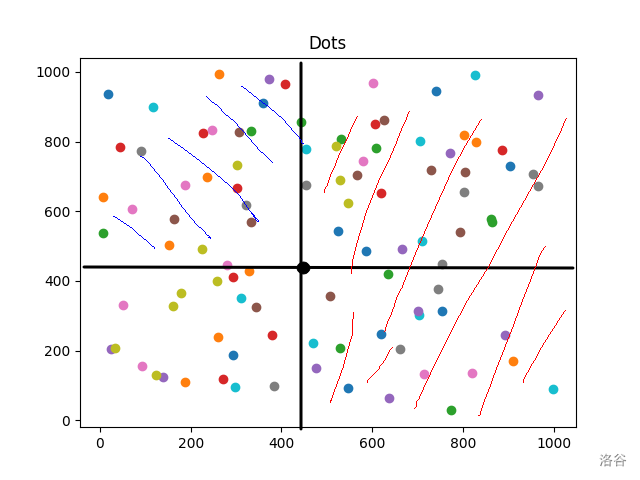
红色部分是右侧的点，蓝色部分是左上方的点。

具体边界参考题目！

我们需要求最大的贡献值。

解题

其实不难发现，目标点的横坐标一定是图中某一个点的横坐标，否则我们可以在固定纵坐标的情况下将点向右移，使得贡献变大。

所以问题简化为如何求蓝色部分的最大贡献？

我们先考虑横坐标固定的情况。

设 $f(i)$ 表示左侧部分纵坐标大于 $i$ 的点的个数。那么我们需要求的是

我原本猜测这可能会是一个单峰函数，但是模拟了一组数据：

发现似乎并不单峰……似乎每一次只能暴力求解？

所以我们继续考虑每次加入一个点对于这个函数的影响。

不难发现，其实每一次是把一部分的后缀 $i \times f(i)$ 变为 $(i + 1) \times f(i)$。

而对于后缀的 $+1$，或许可以想到分块打标记~~（逃~~。

而考虑每一个块打了标记之后，我们需要求的其实是 $(i + tag) \times f(i)$ 的值。

考虑设 $b = (i + tag) \times f(i)$，可以转化为 $i \times f(i) = -tag \times f(i) + b$。

在这个式子中最大化 $b$，这是我们思考到斜率优化问题。

具体来说，也就是在每一块中维护一个上凸包，又由于 $tag$ 是递增的……依据斜率维护一个双端队列即可。

然而加入一个点的过程呢？我们直接把它所在的块暴力重构即可。

于是我们可以得到更新后的左侧答案 cans，更新总答案即可。

复杂度分析

这里我尝试使用核算法 (accounting method) 进行分析。

其实代码中有我用英文写的分析……主要是没有配置输入法……

考虑每一次加入一个点，会重构一个块，花费了 $\sqrt n$，而重构凸包，花费是 $2 \times \sqrt n$，其中有一半是提前为凸包中的元素支付的。这使得在一个块中标记的花费为 $0$。也就是说总的复杂度为 $O(n \sqrt n)$。

这么看着复杂度确实不够优秀，所以这需要代码常数优秀才可。

我犯病有 deque 做双端队列……导致开了 O2 才能过。

不过考虑到用 deque 对于边界条件的明示作用更大，所以我还是贴上这个写法。

代码

#include <iostream>
#include <algorithm>
#include <deque>
#include <cmath>

using namespace std;
const int N = 2e5;
typedef long long lint;

// BLO stands for block length, n is the points' count
int BLO, n;

struct P {
	int x, y;
	bool operator < (const P &p) {
		return x < p.x;
	}
} p[N];

int apps[N << 2], apc = 0;
void discrete() {
	static auto gt = greater<int>();
	
	for (int i = 1; i <= n; ++i) {
		apps[i] = p[i].y;
	}
	
	sort(apps + 1, apps + 1 + n, gt);
	int *ae = unique(apps + 1, apps + 1 + n);
	
	for (int i = 1; i <= n; ++i) {
		p[i].y = lower_bound(apps + 1, ae, p[i].y, gt) - apps;
	}
	
	apc = ae - apps - 1;
	BLO = sqrt(apc);
}

void read() {
	cin >> n;
	for (int x, y, i = 1; i <= n; ++i) {
		cin >> x >> y;
		p[i] = {x, y};
	}
	
	sort(p + 1, p + 1 + n);
}

// save the sum of one point
int s[N];
class BLOCK {
private:
	int l, r, tag;
	deque<int> Q; // for using slope optimize
public:
	void set(int l, int r) {
		this->l = l, this->r = r;
	}

	// rebuild this block.
	// with many points that can build a convex tull
	// which can help use maintain the max value.
	inline lint build() {
		lint ans = 0;

		// we calc every point of the BLOCK, to get the answer for whole block after rebuilding.
		for (int i = l; i <= r; ++i) {
			ans = max(ans, 1ll * (s[i] += tag) * apps[i]);
		} tag = 0;

		Q.clear();
		int siz = 0;
		for (int i = r; i >= l; --i) {
#define Y(i) (1ll * apps[i] * (s[i] + tag))
#define X(i) (1ll * apps[i])
			// build reversely, for using the convex hull to right.
			// now add point (X(i), Y(i)), We should make sure slope(i) >= slope(Q[last])
			// Consider Q[siz -1] as j, Q[siz - 2] as k
			// So we need 
			// ( Y(i) - Y(j) ) / ( X(i) - X(j) ) >= ( Y(j) - Y(k) ) / ( X(j) - X(k) )
			// as the followed line
			while (siz > 1 && ( Y(i) - Y(Q[siz -1]) ) * ( X(Q[siz - 1]) - X(Q[siz - 2]) ) >= ( Y(Q[siz - 1]) - Y(Q[siz - 2]) ) * ( X(i) - X(Q[siz - 1]) ))
				Q.pop_back(), --siz;
			Q.push_back(i), ++siz;
		}
		return ans;
	}

	lint add() {
		++tag;
		while (Q.size() > 1 && Y(Q[0]) <= Y(Q[1]))
			Q.pop_front();
		return Y(Q[0]);
	}
} blocks[700];

lint cans = 0;
// now we consider why the complexity is correct?
// we using accounting method to analyze it.
// First, every time we rebuild a block, we cost sqrt(n) to build
// and we build a deque, which at most have sqrt(n) items
// This cost 2*sqrt(n) (half prepayed for adding tag).
// so when we are adding tag, we cost nothing.
// Second, when querying, we use O(1) however.
// In total, we have n times add, which makes complexity to O(n \sqrt n)
inline void add(int y) {
	int b = y / BLO;
	int r = min((b + 1) * BLO, apc + 1); // without r

	// update one block's s and need rebuild!!
	for (int i = y; i < r; ++i) {
		++s[i];
	}

	cans = max(cans, blocks[b].build());
	for (int i = b + 1, ie = apc / BLO; i <= ie; ++i) {
		cans = max(cans, blocks[i].add());
	}
}

int main() {
	cin.tie(0)->sync_with_stdio(false);

	read();
	discrete();
	for (int i = 0, l = 0, r = BLO - 1; l <= apc; ++i, l += BLO, r += BLO) {
		blocks[i].set(max(l, 1), min(r, apc));
		blocks[i].build();
	}

	lint res = 0;
	for (int i = 1; i <= n + 1; ++i) {
		res = max(res, 1ll * (n - i + 1) * p[i].x + cans); // update ans for (n + 1) times !!!
		if (i <= n) add(p[i].y);
	}

	cout << res << '\n';
	return 0;
}

后记

正如我在开头所说，可以使用 KTT 解决这道题。而且复杂度非常优秀，是 $O(n \log^2 n)$,并且跑不满。

思路却也与此相似。可以发现，其实每一次操作我们是在 $i \times f(i)$ 的基础上加后缀加上一个 $f(i)$ 函数。或者这正也是为什么 KTT 可以做这道题的原因。单纯口胡……