自动搬运

查看原文

来自洛谷，原作者为

	cff_0102 & aqua_qaq | 团子群 185800038 | 如果我死了说明我 AFO 了

搬运于2025-08-24 22:46:55，当前版本为作者最后更新于2023-04-27 00:19:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先，我们定义一种行，叫 cff 行。第一行和最后一行总是 cff 行，而对于任何一行，如果它有一个或两个座位被占用，它也是 cff 行。

如果行 $r_1$ 和 $r_2$ 之间没有其他 cff 行，则它们定义了 cff 区间 $[r_1,r_2]$。cff 区间是闭区间，也就是说一个 cff 行可能属于两个 cff 区间，即这些区间不是互相独立的。在每个 cff 区间中，最多有四个占据的座位，也就是 $(r_1,1),(r_1,2),(r_2,1)$ 或 $(r_2,2)$（因为它们之间没有其他 cff 行）。而要是新的乘客要在这个区间选座位，只有下面八个中的其一是最好的选择：

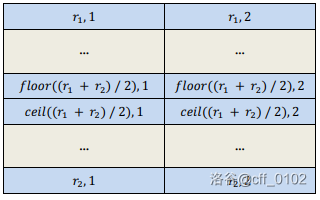
每次乘客进入，判断这八个最好的那个就行了。

当一个人进来时，应该选择哪个 cff 区间呢？应该选择具有最大距离（按上述方法计算而来）的那个 cff 区间，如果有多个这样的 cff 区间，那么应该选择最靠近入口的最佳座位所在的 cff 区间。因此，可以维护一个按照这些标准进行排序的优先队列来保存 cff 区间。

当一个人进入或离开时，我们可能需要更新某些 cff 区间：更新一个 cff 区间，或将一个 cff 区间分成两个 cff 区间，或将两个 cff 区间连接成一个 cff 区间。在所有这些情况下，我们需要从优先队列中删掉一个（或两个）cff 区间并插入一个（或两个）新的 cff 区间。

为了维护 cff 行，我们只需要几个数组：对于每一行，我们记录谁坐在那里，如果这一行是 cff 行，我们还需要记下前一个和后一个 cff 行，以及它属于哪些区间。这些信息足以找到所有 cff 区间，并成功地更新它们。程序只要在一位乘客进入的时候像上面那样判断和输出就可以了。

以下是官方题解代码：

// CEOI 2013 - Task: Tram - Solution
// Author: Luka Kalinovcic

#include <cstdio>
#include <map>
#include <set>
#include <vector>

using namespace std;

typedef long long llint;

llint const oo = 1000000000000000000LL;

struct Point {
  int r, c;
  Point() : r(0), c(0) {}
  Point(int r, int c) : r(r), c(c) {}
};

llint Dist(Point const& A, Point const& B) {
  llint dr = A.r - B.r;
  llint dc = A.c - B.c;
  return dr * dr + dc * dc;
}

struct Candidate {
  Point point;
  llint dist;
};

bool operator<(Candidate const& A, Candidate const& B) {
  if (A.dist != B.dist) return A.dist > B.dist;
  if (A.point.r != B.point.r) return A.point.r < B.point.r;
  return A.point.c < B.point.c;
}

struct Segment;

struct Row {
  int r;
  bool c1_occupied;
  bool c2_occupied;
  Segment *up, *down;

  Row(int r)
      : r(r), c1_occupied(false), c2_occupied(false),
        up(NULL), down(NULL) {}
};

struct Segment {
  Row* row1, *row2;
  Candidate best_seat;

  Segment(Row* row1, Row* row2)
      : row1(row1),
        row2(row2) {
    ResetBestSeat();
    row1->down = this;
    row2->up = this;
  }

  void ResetBestSeat() {
    best_seat.point = Point(row1->r, 1);
    best_seat.dist = 0;
  }

  void FindBestSeat() {
    ResetBestSeat();
    vector<Point> occupied;
    int r1 = row1->r;
    int r2 = row2->r;
    if (row1->c1_occupied) occupied.push_back(Point(r1, 1));
    if (row1->c2_occupied) occupied.push_back(Point(r1, 2));
    if (row2->c1_occupied) occupied.push_back(Point(r2, 1));
    if (row2->c2_occupied) occupied.push_back(Point(r2, 2));
    vector<Point> candidates;
    candidates.push_back(Point(r1, 1));
    candidates.push_back(Point(r1, 2));
    candidates.push_back(Point((r1 + r2) / 2, 1));
    candidates.push_back(Point((r1 + r2) / 2, 2));
    candidates.push_back(Point((r1 + r2 + 1) / 2, 1));
    candidates.push_back(Point((r1 + r2 + 1) / 2, 2));
    candidates.push_back(Point(r2, 1));
    candidates.push_back(Point(r2, 2));
    for (int i = 0; i < (int)candidates.size(); ++i) {
      Candidate seat;
      seat.point = candidates[i];
      seat.dist = oo;
      for (int j = 0; j < (int)occupied.size(); ++j) {
        llint dist = Dist(candidates[i], occupied[j]);
        if (dist < seat.dist) seat.dist = dist;
      }
      if (seat < best_seat) best_seat = seat;
    }
  }
};

struct BestSeatCmp {
  bool operator()(Segment* seg1, Segment* seg2) {
    if (seg1->best_seat < seg2->best_seat) return true;
    if (seg2->best_seat < seg1->best_seat) return false;
    return seg1->row1->r < seg2->row1->r;
  }
};

map<int, Row*> rows;

set<Segment*, BestSeatCmp> segments;

void UpdateSegment(Segment* seg) {
  if (!seg) return;
  segments.erase(seg);
  seg->FindBestSeat();
  segments.insert(seg);
}

void DeleteSegment(Segment* seg) {
  if (!seg) return;
  segments.erase(seg);
  delete seg;
}

int cff_0102[542457];

int main() {
  int N, M;
  scanf("%d%d", &N, &M);
  rows[1] = new Row(1);
  rows[N] = new Row(N);
  segments.insert(new Segment(rows[1], rows[N]));
  UpdateSegment(rows[1]->down);

  vector<Point> points(M);
  for (int i = 0; i < M; ++i) {
    char op;
    scanf(" %c", &op);
    if (op == 'E') {
      Segment* seg = *segments.begin();
      points[i] = seg->best_seat.point;
      int r = points[i].r;
      int c = points[i].c;
      printf("%d %d\n", r, c);
      Row* row;
      if (rows.count(r)) {
        row = rows[r];
      } else {
        Row* row1 = seg->row1;
        Row* row2 = seg->row2;
        DeleteSegment(seg);
        row = new Row(r);
        rows[r] = row;
        segments.insert(new Segment(row1, row));
        segments.insert(new Segment(row, row2));
      }
      if (c == 1) {
        row->c1_occupied = true;
      } else {
        row->c2_occupied = true;
      }
      UpdateSegment(row->up);
      UpdateSegment(row->down);
    } else {
      int x;
      scanf("%d", &x); --x;
      int r = points[x].r;
      int c = points[x].c;
      Row* row = rows[r];
      if (c == 1) {
        row->c1_occupied = false;
      } else {
        row->c2_occupied = false;
      }
      if (r != 1 && r != N && !row->c1_occupied && !row->c2_occupied) {
        Row* row1 = row->up->row1;
        Row* row2 = row->down->row2;
        DeleteSegment(row->up);
        DeleteSegment(row->down);
        rows.erase(r);
        delete row;
        segments.insert(new Segment(row1, row2));
        UpdateSegment(row1->down);
      } else {
        UpdateSegment(row->up);
        UpdateSegment(row->down);
      }
    }
  }
  return 0;
}

官方题解中使用了 set 来搞优先队列。另外，官方代码中的 oo 表示无限（$\infty$）。很轻松地 A 了这题。