自动搬运

查看原文

来自洛谷，原作者为

	phigos **

搬运于2025-08-24 22:46:50，当前版本为作者最后更新于2023-08-29 10:44:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题意简化

给出 $n$ 个 $len\leq600$，仅由 $L$ 和 $P$ 构成的字符串，将 $L$ 看做左括号，$P$ 看做右括号。

求任意两个串 $a$ 和 $b$ 收尾相接后，本质不同的合法括号序列的个数。

思路

设左括号价值为 $1$，右括号价值为 $-1$，那么一个序列合法的充要条件是：

1. 任意前缀的价值和非负

2. 总价值为 $0$

3. 任意后缀的价值和非正

考虑将 $a$ 与 $b$ 拼接后的序列的一个子序列分成前缀和后缀，使得前缀在 $a$ 中，后缀在 $b$ 中，那么就可以分别在 $a$ 和 $b$ 中求出价值为 $k$ 和 $-k$ 的子序列的方案数。

dp

对于 $a$ 串，设 $front_{a,j,k,0/1/2}$ 表示 $a$ 串中，考虑前 $j$ 位，价值和为 $k$，且以左括号 $/$ 右括号 $/$ 空串结尾的方案数。

对于 $b$ 串，设 $back_{b,j,k,0/1/2}$ 表示 $b$ 中，考虑后 $len-j+1$ 位，价值和为 $-k$，且以左括号 $/$ 右括号 $/$ 空串开头的方案数。

初始化

显然，初始为空串，只有一种情况，即：

$$front_{a,0,0,2}=1$$ $$back_{b,0,0,2}=1$$

考虑如何转移

若当前位置 $j$ 为 $'('$：

$$front_{a,j,k,0}\gets front_{a,j-1,k-1,0/1/2}$$ $$back_{b,j,k,0}\gets back_{b,j+1,k+1,0/1/2}$$

若当前位置 $j$ 为 $')'$：

$$front_{a,j,k,1}\gets front_{a,j-1,k+1,0/1/2}$$ $$back_{b,j,k,1}\gets back_{b,j+1,k-1,0/1/2}$$

去重

但如果直接将 $front$ 和 $back$ 乘起来统计答案会重复。

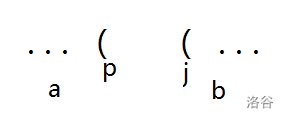
如图，选择 $a$ 中 $p$ 左侧加上 $b$ 以 $j$ 开头的情况，会和选择 $a$ 中以 $p$ 结尾加上 $b$ 中 $j$ 右侧的情况重复。

因此还需要一个数组 $g_{a,j,k,0/1,0/1}$ 表示 $a$ 串中，考虑前 $j$ 位，价值和为 $k$，$j$ 右侧是否有左括号，是否有右括号的方案数。

设 $l/r$ 为 $j$ 右侧剩余的左or右括号数，就有：

$j$ 位置为左括号：

$$g_{a,j,k,l>0,r>0}\gets g_{a,j-1,k,l>0,r>0}+front_{a,j-1,k-1,0/1/2}-front_{a,j-1,k,0} $$

$j$ 位置为右括号：

$$g_{a,j,k,l>0,r>0}\gets g_{a,j-1,k,l>0,r>0}+front_{a,j-1,k+1,0/1/2}-front_{a,j-1,k,1} $$

像这样，只要 $a$ 串后面没有 $b$ 串开头的括号，就不会出现上面的重复情况。

统计答案

设答案为 $ans$。

若 $b$ 串以左括号开头，那么 $a$ 的末尾不能有左括号； 若 $b$ 串以右括号开头，那么 $a$ 的末尾不能有右括号； 若 $b$ 串为空串，那么 $a$ 没有限制。

$$ans\gets (g_{a,n,k,0,0}+g_{a,n,k,0,1})\times back_{b,1,k,0} $$$$ans\gets (g_{a,n,k,0,0}+g_{a,n,k,1,0})\times back_{b,1,k,1} $$$$ans\gets (g_{a,n,k,0,0}+g_{a,n,k,0,1}+g_{a,n,k,1,0}+g_{a,n,k,1,1})\times back_{b,1,k,2} $$

空间优化

不难发现，三个 $dp$ 数组都要开到 $n^3$，喜提MLE。

但是，对于 $j$ 这一维，我们每次转移都只用到了前一位的结果，并且统计答案只用到 $j=n$，因此可以通过调整循环的方向压掉 $j$ 这一维。

时间复杂度为 $O(n^3)$，可以通过本题。

记得取模！！！

代码

#include<bits/stdc++.h>
#define int long long
#define inf (1ll<<60)
using namespace std;
const int N=605,mod=1e9+7;
int n,front[N][N][3],back[N][N][3],g[N][N][2][2];
char s[N];
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>(s+1);
		int num=strlen(s+1);
		int l=0,r=0;
		for(int j=1;j<=num;j++) s[j]=='L'?l++:r++;//j右侧左/右括号的个数
		front[i][0][2]=1;
		back[i][0][2]=1;
		g[i][0][(bool)l][(bool)r]=1;
		for(int j=1;j<=num;j++){//正序处理前缀
			if(s[j]=='L'){l--;
				for(int k=600;k>=1;k--){
					(g[i][k][(bool)l][(bool)r]+=front[i][k-1][0]+front[i][k-1][1]+front[i][k-1][2]-front[i][k][0]+mod)%=mod;
					(front[i][k][0]=front[i][k-1][0]+front[i][k-1][1]+front[i][k-1][2])%=mod;
				}
			}else{r--;
				for(int k=0;k<600;k++){
					(g[i][k][(bool)l][(bool)r]+=front[i][k+1][0]+front[i][k+1][1]+front[i][k+1][2]-front[i][k][1]+mod)%=mod;
					(front[i][k][1]=front[i][k+1][0]+front[i][k+1][1]+front[i][k+1][2])%=mod;
				}
			}
		}
		for(int j=num;j>=1;j--){//倒序处理后缀
			if(s[j]=='L')
				for(int k=0;k<600;k++)
					(back[i][k][0]=back[i][k+1][0]+back[i][k+1][1]+back[i][k+1][2])%=mod;
			else
				for(int k=600;k>=1;k--)
					(back[i][k][1]=back[i][k-1][0]+back[i][k-1][1]+back[i][k-1][2])%=mod;
		}
	}
	for(int i=1;i<=n;i++){//枚举a串
		for(int j=1;j<=n;j++){//枚举b串
			int ans=mod-1;
			for(int k=0;k<=600;k++){
				(ans+=(g[i][k][0][0]+g[i][k][0][1])*back[j][k][0]%mod)%=mod;
				(ans+=(g[i][k][0][0]+g[i][k][1][0])*back[j][k][1]%mod)%=mod;
				(ans+=(g[i][k][0][0]+g[i][k][0][1]+g[i][k][1][0]+g[i][k][1][1])*back[j][k][2]%mod)%=mod;
			}
			cout<<ans<<' ';
		}
		putchar('\n');
	}
	return 0;
}