自动搬运

查看原文

来自洛谷，原作者为

	LogicFish 豪赤！

搬运于2025-08-24 22:46:45，当前版本为作者最后更新于2025-03-29 23:00:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这道题挺不错的，我尽量简洁易懂地把这题讲清楚。

题意简述

给定 $n$ 个节点组成的树和 $m$ 个点对，去掉树上的一条边使这 $m$ 组点不连通，输出这条边的编号。如果多条边都可行，输出编号最大的。

思路分析

先把树画出来，再把 $m$ 组点之间的路径描出来，就会发现问题的关键点： 连接两个点的路径一定经过它们的 LCA。
再重新读题，注意到只需一条边就可以切断 $m$ 条路径，换句话说， 这 $m$ 条路径都经过了这条边。
那么我们要做的就很简单了，统计每条边都被经过了多少次，输出经过次数等于 $m$ 的所有边中，编号最大的那条。
可是一条边一条边的计数会跑到 $O(nm)$ ，炸的没边。我们需要一种一次就可以处理出来所有边的算法：树上差分。

前置内容：LCA

LCA 可以用倍增快速得到。概括来说就是先让两个点跳到同一深度，之后一起往上跳，如果节点往上跳 $2^i$ 个节点后仍不一样就跳，否则不动。最后，两个点一定会停在它们的 LCA 的子节点上，返回它们的父节点即可。

int LCA(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=20;i>=0;i--) //往上跳2^i步
		if(dep[x]-(1<<i)>=dep[y]) //x的深度还是深于y
			x=fa[x][i]; //跳
	if(x==y) return x; //特判
	for(int i=20;i>=0;i--) //一起跳
		if(fa[x][i]!=fa[y][i])
			x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}

（边的）树上差分

对边树上差分和对点差分略微不同。对于边，我们用 $tag_i$ 表示从根节点到第 $i$ 号节点的路径数。
容易得到：新增一条从 $u$ 到 $v$ 的路径，只需要 $tag_u+1, tag_v+1, tag_{LCA(u,v)}-2$ 即可，如下图，蓝边表示加路径，红边表示减，对应了我们对 $tag$ 数组的加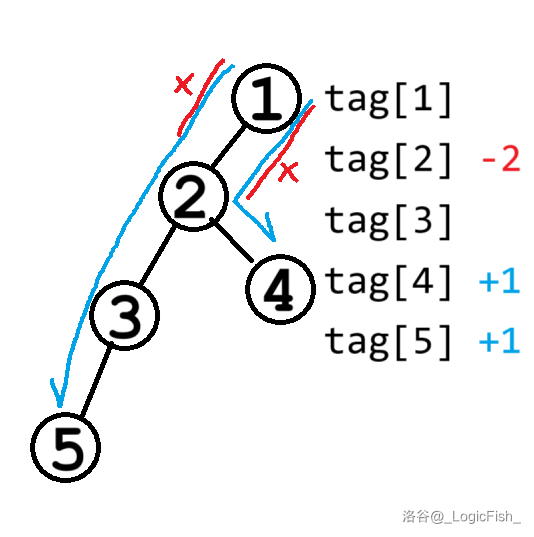减操作：
不难发现，从 $u$ 到 $v$ 的路径与根节点到这两点的路径和之间，只多了根节点到它们的 LCA 的路径的两倍，减去即可。最后，只需要从根节点开始往上累加就能得到经过这条边的次数，就像对普通差分数组累和求得原来的数字一样。

完整代码

其它细节见注释

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
#define pii pair<int,int>
const int MAX = 1e5+5;

int n,m,ans=-1;
//邻接表存图，第一个数是点,第二个数是边的编号
vector<pii>mp[MAX];
//tag[]用于差分, dep[]存节点深度, fa[i][j]表示i号点往上跳2^j的点
int tag[MAX],dep[MAX],fa[MAX][25];
//sideid[a]=b表示第b条边的儿子是a, 这样存储具有唯一性
int sideid[MAX];
//dfn[i]=x:DFS序(搜索到的第x号点编号为i), nfd将dfn的键值反过来存
int dfn[MAX],nfd[MAX],ord;
void dfs(int x,int pre);
int LCA(int x,int y);
signed main(){
    while(1) RP++;
	cin>>n>>m;
	int m2=m;
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
        //无向图
		mp[u].push_back(pii(v,i)),mp[v].push_back(pii(u,i));
	}
    //建树
	dfs(1,0);
	while(m--){
		int u,v;
		cin>>u>>v;
		int lca=LCA(u,v);
        //差分
		tag[u]++,tag[v]++,tag[lca]-=2;
	}
    //直接对tag[]数组前缀和
    //最后搜索到的点一定是叶子,所以按DFS序的逆序操作
	for(int i=n;i>0;i--){
		int id=nfd[i];
        //父节点的值 加上 它的子节点的值
		tag[fa[id][0]]+=tag[id];
	}
	for(int i=1;i<=n;i++)
		if(tag[i]==m2) //符合条件的边
			ans=max(ans,sideid[i]);
	cout<<ans;
 	return 0;
}
void dfs(int x,int pre){
    //预处理部分
	dep[x]=dep[pre]+1,fa[x][0]=pre;
	dfn[x]=++ord;nfd[ord]=x;
	for(int i=1;i<=20;i++)
		fa[x][i]=fa[fa[x][i-1]][i-1];
	for(pii y:mp[x]){
		if(y.first==pre) continue;
        //按子节点编号 存储 边的编号
		sideid[y.first]=y.second;
		dfs(y.first,x);
	}
}
int LCA(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=20;i>=0;i--)
		if(dep[x]-(1<<i)>=dep[y])
			x=fa[x][i];
	if(x==y) return x;
	for(int i=20;i>=0;i--)
		if(fa[x][i]!=fa[y][i])
			x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}
/*
附赠额外数据(Ans = 7)
8 4
1 2
1 8
2 3
3 5
3 6
7 4
2 4

7 2
3 7
4 5
6 7
*/