自动搬运

查看原文

来自洛谷，原作者为

	AFewSuns 弱省弱校蒟蒻，tcl，zbl

搬运于2025-08-24 22:46:14，当前版本为作者最后更新于2023-04-07 12:40:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

很套路的一道题。

题目大意

给定长为 $n$ 的序列 $a$，$a_i$ 互不相同。你要将其重排成 $f_1,f_2,\dots,f_n$，需要满足 $|f_1-f_2|+|f_2-f_3|+\dots+|f_{n-1}-f_n| \leq L$，求满足条件的重排方案数，对 $10^9+7$ 取模。

$1 \leq n \leq 100,1 \leq L,a_i \leq 1000$

题目分析

首先把重排后的序列 $f$ 拍到平面上，横坐标为下标，纵坐标为 $f_i$，如下图：

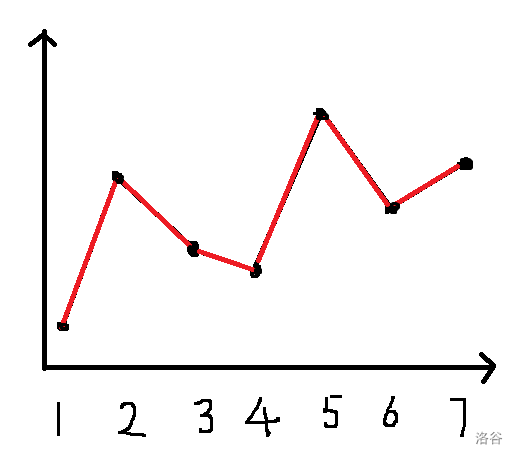
那么所要求的就是红线的（纵坐标差）长度和。容易想到从上往下扫，然后动态计算目前的折线长度和：

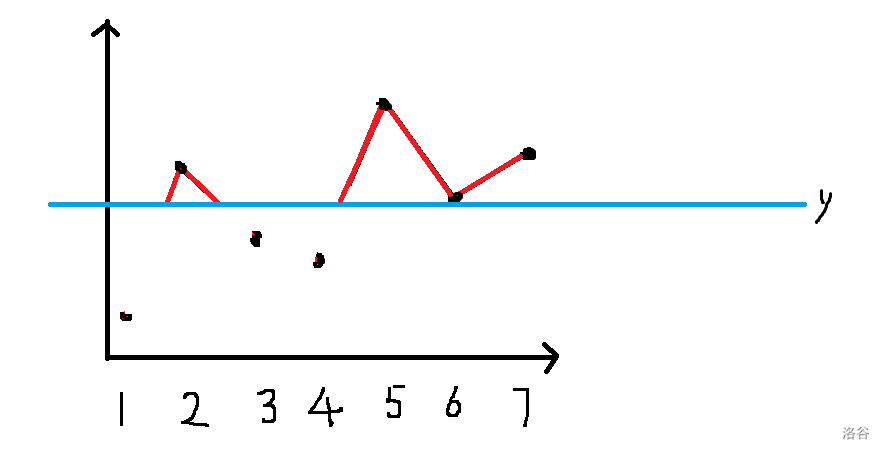
每次从大到小加入 $a_i$，那么新增加的折线就有 $2 \times$ 目前连续段数个（下图绿色部分）：

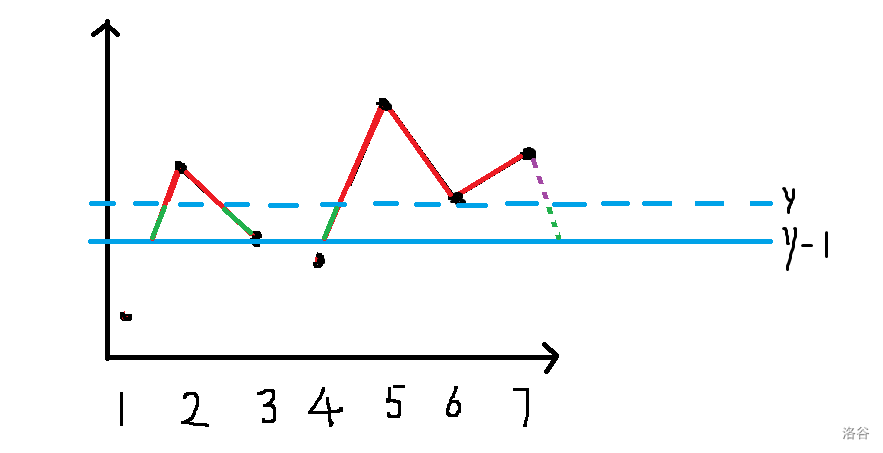
不过注意到当最后一个数已经插入时，后面不能再算贡献（绿色紫色虚线部分），同理，第一个数已经插入时前面不能再算贡献。于是设 $dp_{i,j,0/1,0/1}$ 表示目前已经有 $i$ 个连续段，答案为 $j$，第一个数/最后一个数有没有被加进去，答案就是 $dp_{1,\leq L,1,1}$。

转移的话大致有三种：

• 这个数新开了一个段，段数 $+1$。
• 这个数合并了两段，段数 $-1$。
• 这个数延续了其中一段，段数不变。

时间复杂度 $\mathcal O(n^2L)$，足以通过。

代码

#include<bits/stdc++.h>
#define mod 1000000007
#define ll long long
#define fr(i,x,y) for(register ll i=(x);i<=(y);i++)
using namespace std;
ll n,lim,a[110],f[110][1010][2][2],g[110][1010][2][2],ans=0;
inline void inc(ll &x,ll y){
	((x+=y)>=mod)?(x-=mod):0;
}
int main(){
	scanf("%lld %lld",&n,&lim);
	fr(i,1,n) scanf("%lld",&a[i]);
	sort(a+1,a+n+1);
	reverse(a+1,a+n+1);//从大到小排序 
	fr(p,0,1) fr(q,0,1) f[1][0][p][q]=1;
	fr(i,2,n){
		fr(j,1,i-1) fr(k,0,lim) fr(p,0,1) fr(q,0,1) g[j][k][p][q]=f[j][k][p][q];
		fr(j,1,i-1) fr(k,0,lim) fr(p,0,1) fr(q,0,1) f[j][k][p][q]=0;
		fr(j,1,i-1){
			fr(k,0,lim){
				fr(p,0,1){
					fr(q,0,1){
						if(!g[j][k][p][q]) continue;
						ll kk=k+(2*j-p-q)*(a[i-1]-a[i]);
						if(kk>lim) continue;
						//新开一个段 
						if(j>1) inc(f[j+1][kk][p][q],(j-1)*g[j][k][p][q]%mod);//在中间开段 
						if(!p){//在最左边开段 
							inc(f[j+1][kk][0][q],g[j][k][p][q]);
							inc(f[j+1][kk][1][q],g[j][k][p][q]);
						}
						if(!q){//在最右边开段 
							inc(f[j+1][kk][p][0],g[j][k][p][q]);
							inc(f[j+1][kk][p][1],g[j][k][p][q]);
						}
						//延续一段 
						if(j>1) inc(f[j][kk][p][q],2*(j-1)*g[j][k][p][q]%mod);
						if(!p){
							inc(f[j][kk][0][q],g[j][k][p][q]);
							inc(f[j][kk][1][q],g[j][k][p][q]);
						}
						if(!q){
							inc(f[j][kk][p][0],g[j][k][p][q]);
							inc(f[j][kk][p][1],g[j][k][p][q]);
						}
						//合并两段 
						if(j>1) inc(f[j-1][kk][p][q],(j-1)*g[j][k][p][q]%mod);
					}
				}
			}
		}
	}
	fr(i,0,lim) ans=(ans+f[1][i][1][1])%mod;
	printf("%lld",ans);
}