1 条题解
-
0
自动搬运
来自洛谷,原作者为

buzhidao
逃避者不配拥有未来. || 不蓝勾不改个签搬运于
2025-08-24 22:46:01,当前版本为作者最后更新于2023-06-28 15:45:13,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题目分析
其实贪心不会超时,就是不能通过,详见这里。
这道题可以根据 的填写顺序,列成一张表。图可能有点丑。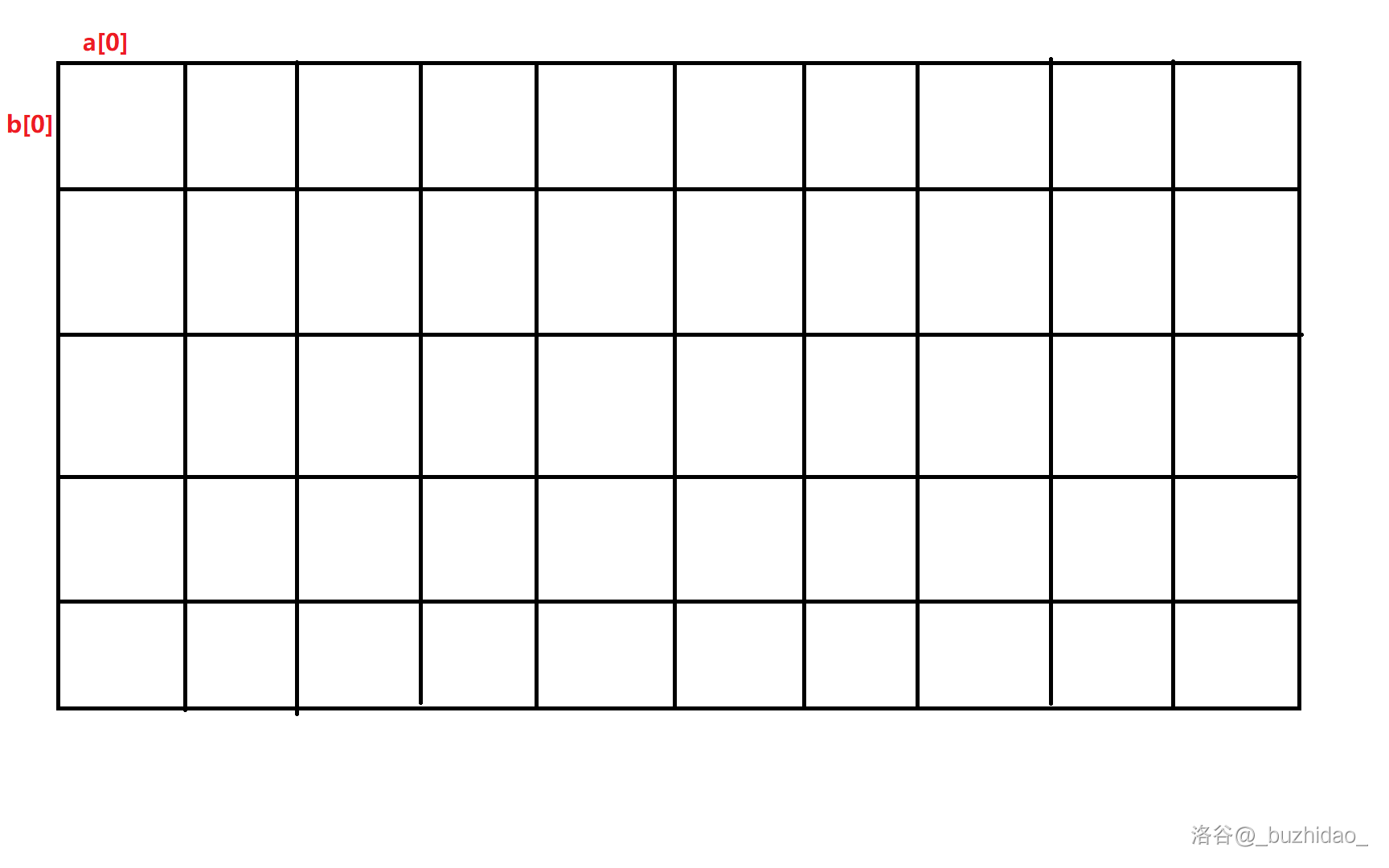 显然,我们要从左上角移动到右下角,把 全部填写完。
显然,我们要从左上角移动到右下角,把 全部填写完。
我们只能向下或向右走。如果把所有路径都尝试一遍,就成了递归,必然超时。所以我们需要——
动态规划
大小:,最大占用 空间,小于题目限制。
表示 数组填写 个数, 数组填写 个数, 数组当前的最大值。
表示 数组填写 个数, 数组填写 个数, 数组当前的最大值。例如:
,已知 。目标:填充全部。可结合表格分析。
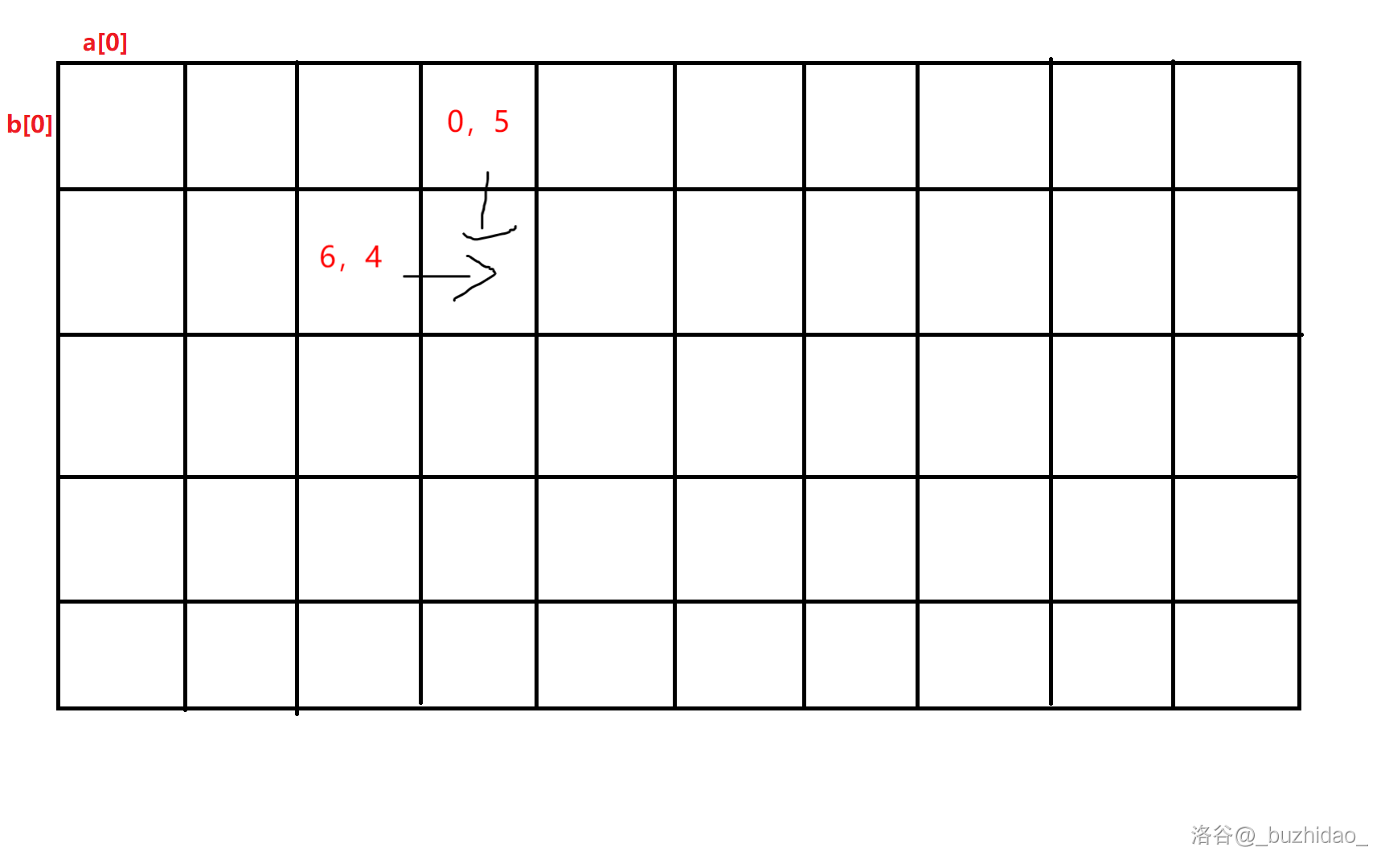
- 路径 :从 开始填写:因为 ,所以 。
- 路径 :从 开始填写:因为 ,所以 。
综上,因为要取最小值,所以得到答案 。
递推公式
初始化为 。
当 :
- 当 :,否则 。
- 当 :,否则 。
当 :
- 当 :,否则 。
- 当 :,否则 。
AC代码
#include<bits/stdc++.h> using namespace std; int dp[5005][5005][2]; int n,m,a[5005],b[5005]; const int inf=1e9; int main(){ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);//IO优化 cin>>n;for(int i=1;i<=n;++i) cin>>a[i]; cin>>m;for(int i=1;i<=m;++i) cin>>b[i]; for(int i=0;i<=n;++i){ for(int j=0;j<=m;++j){ if(i==0&&j==0) continue;//这种情况不存在 dp[i][j][0]=inf; //为防止代码过长,加以适当简化 if(i){ dp[i][j][0]=min(dp[i][j][0],dp[i-1][j][0]+1+(bool)(a[i]==a[i-1])); dp[i][j][0]=min(dp[i][j][0],dp[i-1][j][1]+1+(bool)(a[i]==b[j])); } dp[i][j][1]=inf; if(j){ dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][1]+1+(bool)(b[j]==b[j-1])); dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][0]+1+(bool)(b[j]==a[i])); } } } cout<<min(dp[n][m][0],dp[n][m][1]);//输出最优方案 return 0; }
- 1
信息
- ID
- 8393
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 3
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
