1 条题解
-
0
自动搬运
来自洛谷,原作者为
tiger2005
Failure, as usual.搬运于
2025-08-24 22:45:45,当前版本为作者最后更新于2023-03-08 01:09:22,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
不得不说,这道题目扔到一个 4.5 小时的 ACM 竞赛里面确实有些丧尽天良了.jpg
0x00 题意
你需要模拟一系列非常复杂的空中战争系统,具体请仔细阅读原题信息。
0x01 向量
这道题目的状态绕不开三维向量,故我们需要实现一个基础的三维向量类,以及一些基础的数学函数:
const double PI = -acos(-1.0); const double EPS = 1e-9; bool isZero (double x) { return abs(x) < EPS; } double clamp (double x) { return max(-1.0, min(x, 1.0)); } struct Vec3 { double x, y, z; Vec3 (double x, double y, double z) :x(x), y(y), z(z) {} Vec3 () { x = y = z = 0; } double Dot (Vec3 v) { return x * v.x + y * v.y + z * v.z; } Vec3 Cross (Vec3 v) { return Vec3( y * v.z - z * v.y, z * v.x - x * v.z, x * v.y - y * v.x ); } double Length () { return sqrt(x * x + y * y + z * z); } Vec3 operator - () { return Vec3 (-x, -y, -z); } Vec3 operator + (Vec3 v) { return Vec3 ( x + v.x, y + v.y, z + v.z ); } Vec3 operator * (double len) { return Vec3 (x * len, y * len, z * len); } Vec3 operator / (double len) { return *this * (1 / len); } Vec3 Norm () { return (*this) / (*this).Length(); } Vec3 operator - (Vec3 v) { return *this + (-v); } double Angle (Vec3 v) { return acos(clamp(Dot(v))); } bool _isZero () { return isZero(Length()); } void init () { scanf(" %lf %lf %lf", &x, &y, &z); } };注意在将点乘结果套入
acos()函数前,需要先clamp()一下,防止结果小于 -1 导致返回nan。这道题涉及到点到线段的距离,以及三维向量到面的映射。前者可以通过分类讨论解决,后者只需要通过点乘计算出在单位向量的分向量,故有:
double minLength (Vec3 a, Vec3 b, Vec3 c) { Vec3 ca = a - c, cb = b - c, ab = b - a; if (ca.Dot(ab) > 0) return ca.Length(); if (ab.Dot(cb) < 0) return cb.Length(); return ca.Cross(cb).Length() / ab.Length(); } pair<double, double> Alpha (Vec3 x, Vec3 y, Vec3 p) { return make_pair(x.Dot(p), y.Dot(p)); }0x02 无人机
先定义类:
struct Plane { Vec3 p, d, u, l; int id, from; bool crashed; int target; double tu, td, gm, v, lx, hy; Vec3 strategy; };考虑计算将飞机移动到一个位置时的代价。根据题目条件,显然可以得到:一个合法移动应该是所有到达同等位置的移动中最快的,故不会停停走走,而是连续进行操作到达目的地。代价需要分三部分计算:
- 滚动:考虑到在滚动后 需要垂直于 和 形成的面上,故先计算出这个面的法向量(只需要一次叉乘),判断是否需要翻转后计算和 的夹角即可。此处需要特判 和 平行的情况,在这个情况下可以不滚动。
- 俯仰:直接计算 和 的夹角即可。
- 直线移动:直接计算位置距离即可。
那么我们可以写出估价和移动代码:
double planeMoveCost (Plane &p, Vec3 delta) { Vec3 dir = delta.Norm(); Vec3 L = p.d.Cross(dir); if (L._isZero()) L = p.l; else { L = L.Norm(); if (L.Dot(p.l) < 0) L = - L; } double SpinTo = L.Angle(p.l); double RotateTo = p.d.Angle(dir); return SpinTo / p.gm + RotateTo / (p.u.Dot(dir) >= 0 ? p.tu : p.td) + delta.Length() / p.v; } void planeMoveTo (Plane &p, Vec3 delta) { if (delta._isZero()) { swap(p.u, p.d); p.u = - p.u; return; } p.p = p.p + delta; Vec3 dir = delta.Norm(); Vec3 L = p.d.Cross(dir); if (L._isZero()) L = p.l; else { L = L.Norm(); if (L.Dot(p.l) < 0) L = - L; } p.d = dir; p.l = L; p.u = p.d.Cross(p.l); }0x03 导弹
依然先定义类:
struct Missle { Vec3 p, d; double tr, v, ds, dp, bs; bool activated; bool explosive; bool used; bool lost; int target; int tz; int id; Vec3 strategy; };导弹的代价计算相对简单,偏航角度就是两个飞行方向的夹角,长度也很好算,故有:
double missleMoveCost (Missle& m, Vec3 delta) { Vec3 dir = delta.Norm(); double SpinTo = m.d.Angle(dir); return SpinTo / m.tr + delta.Length() / m.v; } void missleMoveTo (Missle &m, Vec3 delta) { m.p = m.p + delta; Vec3 dir = delta.Norm(); m.d = dir; -- m.tz; }0x04 策略
无人机需要在时刻开始时确定目标。根据题目的分布条件,我们可以编写一些辅助函数,从而快速实现。
其中,判定视野直接利用题目公式点乘判断即可,判断雷达也可以利用前面实现的
Alpha()函数计算。我们可以通过“需不需要换 -> 有没有雷达区内的 -> 有没有视野内的”的顺序枚举并判断。bool inView (Plane &p, Plane &q) { return p.d.Dot(q.p - p.p) > EPS; } bool detective (Plane &p, Plane &q) { if (! inView(p, q)) return false; pair<double, double> loc = Alpha(p.l, p.u, q.p - p.p); return abs(loc.first) <= p.lx + EPS && abs(loc.second) <= p.hy + EPS; } void planeChoose (Plane &p) { if (p.target != 0 && !planes[p.target].crashed && inView(p, planes[p.target])) return; p.target = 0; double q1 = 1e18; int id = -1; for (int i = 1; i <= 2 * N; i ++) { if (i == p.id || planes[i].crashed || planes[i].from == p.from) continue; if (detective (p, planes[i])) { double val = (p.p - planes[i].p).Length(); if (q1 - val > EPS) { q1 = val; id = i; } } } if (id != -1) { p.target = id; return; } q1 = 1e18, id = -1; for (int i = 1; i <= 2 * N; i ++) { if (i == p.id || planes[i].crashed || planes[i].from == p.from) continue; if (inView (p, planes[i])) { pair<double, double> loc = Alpha(p.l, p.u, planes[i].p - p.p); double val = min(abs(loc.first - p.lx), abs(loc.first + p.lx)) + min(abs(loc.second - p.hy), abs(loc.second + p.hy)); if (q1 - val > EPS) { q1 = val; id = i; } } } if (id != -1) { p.target = id; return; } }随后就是策略选择。考虑到每个时刻前后无人机只会出现在整点处,而 范围并不大,故可以直接枚举附近的整点,判断代价后借助题目提供的流程翻译成对应代码就好了。相信来到这一步,你对题目设计的专业名词已经很熟悉了!
代码中
Vec(0, 0, 0)代表眼镜蛇机动标识,因为一个合法的机动必然需要移动。void planeStrategy (Plane &p) { if (!p.target) p.strategy = Vec3 (0, 0, 0); else { Plane q = planes[p.target]; int P = floor(p.v); Vec3 cur; double q1 = 1e18, q2 = 1e18; vector<pair<Vec3, Plane> > vs; for (int i = - P; i <= P; i ++) for (int j = - P; j <= P; j ++) for (int k = - P; k <= P; k ++) if ((i != 0 || j != 0 || k != 0) && (cur = Vec3(i, j, k)).Length() <= p.v) { Plane np = p; double l = (p.p + cur - q.p).Length(); if (planeMoveCost(np, cur) <= 1.0 + EPS) { planeMoveTo(np, cur); if (inView(np, q)) { if (q1 - l > EPS) vs.clear(), q1 = l; if (isZero(q1 - l)) vs.emplace_back(cur, np); } } } q1 = 1e18; int id = -1; bool det = false; for (int i = 0; i < (int)vs.size(); i ++) { Plane np = vs[i].second; pair<double, double> loc = Alpha(np.l, np.u, q.p - np.p); if (detective(np, q)) { det = true; double val = sqrt(loc.first * loc.first + loc.second * loc.second); if (q1 - val > EPS) q1 = val, id = i; } else if (! det) { double val = min(abs(loc.first - np.lx), abs(loc.first + np.lx)) + min(abs(loc.second - np.hy), abs(loc.second + np.hy)); if (q2 - val > EPS) q2 = val, id = i; } } if (id != -1) p.strategy = vs[id].first; else { Vec3 exp = p.d * p.v; Vec3 str = Vec3(0, 0, 0); for (int i = - P; i <= P; i ++) for (int j = - P; j <= P; j ++) for (int k = - P; k <= P; k ++) if ((i != 0 || j != 0 || k != 0) && (cur = Vec3(i, j, k)).Length() <= p.v) { if (planeMoveCost(p, cur) <= 1.0 + EPS) { double val = (exp - cur).Length(); if (q1 - val > EPS) q1 = val, str = cur; } } p.strategy = str; } } }导弹也需要实现策略。在实现锁定角相关的辅助函数后,这部分代码也不难写出,也不难发现和无人机策略代码类似。
double missleAngle (Missle &m, Plane &p) { Vec3 v = (p.p - m.p).Norm(); return v.Angle(m.d); } bool missleDetective (Missle &m, Plane &p) { if (p.crashed) return false; if (m.d.Dot(p.p - m.p) <= 0) return false; return missleAngle(m, p) <= m.bs; } void missleStrategy (Missle &m) { int P = floor(m.v); Vec3 cur; double q1 = 1e18; if (m.target) { if (!m.lost) { Plane q = planes[m.target]; planeMoveTo(q, q.strategy); vector<pair<Vec3, Missle> > vs; for (int i = - P; i <= P; i ++) for (int j = - P; j <= P; j ++) for (int k = - P; k <= P; k ++) if ((i != 0 || j != 0 || k != 0) && (cur = Vec3(i, j, k)).Length() <= m.v) { Missle nm = m; double l = (m.p + cur - q.p).Length(); if (missleMoveCost(nm, cur) <= 1.0 + EPS) { missleMoveTo(nm, cur); if (isZero(l) || missleDetective(nm, q)) { if (q1 - l > EPS) q1 = l, vs.clear(); if (isZero(q1 - l)) vs.emplace_back(cur, nm); } } } if (isZero(q1)) { m.strategy = vs[0].first; return; } q1 = 1e18; int id = -1; for (int i = 0; i < (int)vs.size(); i ++) { double val = missleAngle(vs[i].second, q); if (q1 - val > EPS) q1 = val, id = i; } if (id != -1) { m.strategy = vs[id].first; return; } } } Vec3 exp = m.d * m.v; Vec3 str = Vec3(0, 0, 0); for (int i = - P; i <= P; i ++) for (int j = - P; j <= P; j ++) for (int k = - P; k <= P; k ++) if ((i != 0 || j != 0 || k != 0) && (cur = Vec3(i, j, k)).Length() <= m.v) { if (missleMoveCost(m, cur) <= 1.0 + EPS) { double val = (exp - cur).Length(); if (q1 - val > EPS) q1 = val, str = cur; } } m.strategy = str; }0x05 发射导弹
无人机在空闲情况下会朝着敌方发射导弹。这一部分其实相当容易实现,只需要新增一个空闲数组即可。
void launchMissle (Plane &p) { if (p.target != 0 && detective(p, planes[p.target]) && !idle[p.id]) { Vec3 _p = planes[p.target].p; Missle m = missleOpts[p.id]; m.p = p.p; m.d = (_p - p.p).Norm(); m.target = p.target; missles.push_back(m); idle[p.id] = true; } }0x06 事件整理
最后根据题目提供时刻事件表,将所有的步骤变成对应的代码,我们就得到了主函数:
vector<int> killList[210]; void generateKillMessage (vector<pair<int, int> > kills) { for (int i = 1; i <= 2 * N; i ++) killList[i].clear(); for (auto l: kills) killList[l.second].push_back(l.first); for (int i = 1; i <= 2 * N; i ++) if (killList[i].size() != 0) { printf("%d %d ", i, (int)killList[i].size()); sort(killList[i].begin(), killList[i].end()); for (auto x: killList[i]) printf("%d ", x); printf("\n"); } } int main() { scanf("%d %d", &N, &T); for (int i = 1; i <= 2 * N; i ++) { planes[i].p.init(); planes[i].d.init(); planes[i].u.init(); planes[i].l = planes[i].u.Cross(planes[i].d); scanf(" %lf %lf %lf %lf %lf %lf", &planes[i].tu, &planes[i].td, &planes[i].gm, &planes[i].v, &planes[i].lx, &planes[i].hy); scanf(" %lf %lf %lf %lf %lf %d", &missleOpts[i].tr, &missleOpts[i].v, &missleOpts[i].ds, &missleOpts[i].dp, &missleOpts[i].bs, &missleOpts[i].tz); planes[i].id = missleOpts[i].id = i; planes[i].from = i <= N; ++ missleOpts[i].tz; } while (T --) { vector<pair<int, int> > kills1(0); vector<pair<int, int> > kills2(0); vector<vector<int> > group(0); int ANS1 = 0, ANS2 = 0; // 所有无人机选定目标,并确定当前时刻内的飞行策略 for (int i = 1; i <= 2 * N; i ++) { if (planes[i].crashed) continue; planeChoose(planes[i]); planeStrategy(planes[i]); } // 所有能发射导弹的无人机发射导弹 for (int i = 1; i <= 2 * N; i ++) { if (planes[i].crashed) continue; launchMissle(planes[i]); } // 所有导弹确定飞行策略并位移,该过程中部分无人机可能被摧毁 for (auto &m: missles) { missleStrategy(m); Vec3 f = m.p, t = m.p + m.strategy; missleMoveTo(m, m.strategy); if (!m.activated) { for (int i = 1; i <= 2 * N; i ++) { if (!planes[i].crashed && (planes[i].p - m.p)._isZero()) { kills1.emplace_back(m.id, i); m.explosive = true; } } } else { for (int i = 1; i <= 2 * N; i ++) { if (!planes[i].crashed && minLength(f, t, planes[i].p) <= m.dp) { kills1.emplace_back(m.id, i); m.explosive = true; } } } } for (auto l: kills1) { if (! planes[l.second].crashed) { planes[l.second].crashed = true; ++ ANS1; } } // 所有可空爆的导弹爆炸并消失 for (auto &m: missles) { if (m.explosive && !m.used) { m.used = true; idle[m.id] = false; } } // 所有无人机按 1. 中确定的飞行策略位移,该过程中部分无人机可能被摧毁 for (int i = 1; i <= 2 * N; i ++) { if (planes[i].crashed) continue; Vec3 f = planes[i].p, t = planes[i].p + planes[i].strategy; planeMoveTo(planes[i], planes[i].strategy); for (auto &m: missles) { if (m.activated && !m.used && minLength(f, t, m.p) <= m.dp) { kills2.emplace_back(m.id, i); m.explosive = true; } else if (!m.activated && !m.used && (m.p - planes[i].p)._isZero()) { kills2.emplace_back(m.id, i); m.explosive = true; } } } for (auto l: kills2) { if (! planes[l.second].crashed) { planes[l.second].crashed = true; ++ ANS2; } } // 所有可空爆的导弹爆炸并消失 for (auto &m: missles) { if (m.explosive && !m.used) { m.used = true; idle[m.id] = false; } } // 所有位置相同的无人机发生碰撞并坠毁 for (int i = 1; i <= 2 * N; i ++) { if (planes[i].crashed) continue; vector<int> v(0); v.push_back(i); for (int j = i + 1; j <= 2 * N; j ++) { if (!planes[j].crashed && (planes[j].p - planes[i].p)._isZero()) v.push_back(j); } if (v.size() > 1) { group.push_back(v); for (auto p: v) planes[p].crashed = true; } } // 所有超过制导时长和脱锁且已激活的导弹消失 for (auto &m: missles) { if (!m.used) { if (!missleDetective(m, planes[m.target])) m.lost = true; if (m.tz == 0 || (m.activated && m.lost)) { m.used = true; idle[m.id] = false; } } } // 所有可激活的导弹被激活 vector<Missle> nms; for (auto &m: missles) { if (!m.used) { if (planes[m.id].crashed || (m.p - planes[m.id].p).Length() > m.ds) m.activated = true; nms.push_back(m); } } missles = nms; printf("%d %d %d\n", ANS1, ANS2, (int)group.size()); generateKillMessage(kills1); generateKillMessage(kills2); for (auto v: group) { printf("%d ", (int)v.size()); for (auto x: v) printf("%d ", x); printf("\n"); } } return 0; }整合后得到最终代码:这里。
0x07 结束了……?
当然没有。这道题目设立了相当多的坑点,稍有不慎就会误入歧途。
- 题目中的制导时长 代表 导弹可以操作进行 最多 次 控制,而不是 次。如果你在每一次控制后将寿命减去 1,千万要主意这点。
- 请注意代码中 的使用!如果你在一些地方缺失了浮点数判断,那么就可能导致目标计算错误而导致偏航!
- 导弹事件的触发机制比较复杂,请不要默认一些操作的条件。
- 这道题目设计了多个函数对一个函数的复用。请注意复用时被调用函数内部变量是否符合预期。
0xff 趣闻
- 这份代码我花了一个晚上(3 小时)写完,又花了一个晚上(4 小时)调试完毕。至于为什么,我相信大家也都知道了。
- 这份代码后半部分调试运用到了官方数据集的正确代码和数据。std 可读性比我的代码差得多了!
- 我在官方数据集下找到了三份 std,随后扔到了 Lemonlime 一起测试,于是:
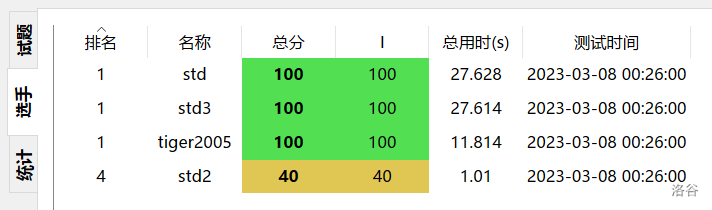
- 1
信息
- ID
- 8472
- 时间
- 5000ms
- 内存
- 1024MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
