自动搬运

查看原文

来自洛谷，原作者为

	周子衡 Shadow is the light!

搬运于2025-08-24 22:45:08，当前版本为作者最后更新于2023-01-17 15:20:34，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

退役！

我们先来猜测无解的条件。注意到在一组合法解中，对固定的某个社团，相邻的 $3$ 个人中最多有 $2$ 个来自该社团。因而每个社团的大小都不应该超过总人数的 $\dfrac{2}{3}$，反之无解。

下面我们来说明上面给出的就是有解的等价条件，并给出一种构造解的算法。

首先需要注意的是，如果每个社团大小都不超过 $2$，那么任意排列都是合法的。接下来我们将讨论至少有一个社团人数不小于 $3$ 的情形。

考虑归纳构造。由于猜测的最佳比例是 $\dfrac{2}{3}$，考虑一次取 $3$ 个人，对剩下的 $n-3$ 个人构造一组解出来。我们不妨规定取出的 $3$ 个人一定要是圆上连续的一段。注意到在存在一个社团大小为 $\dfrac{2}{3}n$ 的极端情况下，构造是非常固定的：

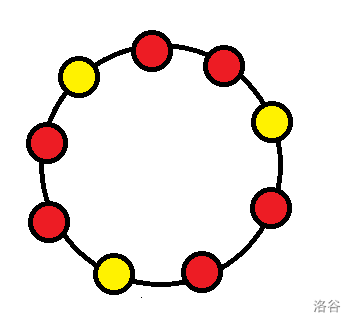
此时任意连续三个人中都有两个来自 大社团，一个不来自 大社团。故我们构造的时候作如下规定：

• 设当前 $n$ 个人中人数最多的社团为 $C$，那么我们选取的 $3$ 人中两人来自 $C$，一人不来自 $C$。

（另外可以注意到，存在一个大社团人数达到 $\dfrac{2}{3}n$ 时，上面图片中的构造一定是正确的。这也是猜测可能成立的迹象之一。）

在继续往下推进之前，我们首先需要保证：剩下 $n-3$ 个人中，不存在占比 $\dfrac{2}{3}$ 的人有相同的社团。注意到由于 $C$ 少了整整 $2$ 个人，那么在剩下的人中 $C$ 的占比必然不超过 $\dfrac{2}{3}$；而对于一个不同于 $C$ 的社团 $D$，注意到原本 $D$ 的人数不超过 $\dfrac{n}{2}$，故我们需要保证 $\dfrac{n}{2}\leq \dfrac{2}{3}(n-3)$ 恒成立，这需要

$$n\geq 12$$

我们稍稍改进一下这个结果。注意到这实际上浪费了“一人不来自 $C$“这里的操作空间，我们让这个人来自剩下的社团中人数最多的那个（记为 $D$），那么 $D$ 的人数不超过 $\dfrac{n}{2}-1$，我们需要保证 $\dfrac{n}{2}-1\leq \dfrac{2}{3}(n-3)$，这只需要 $n\geq 6$ 就够了。而对于 $C,D$ 以外的任意社团 $E$，$E$ 的人数显然不超过 $\dfrac{n}{3}$，我们需要保证 $\dfrac{n}{3}\leq \dfrac{2}{3}(n-3)$，这同样只需要 $n\geq 6$ 即可。而即便不借助计算机，也很容易验证 $n < 6$ 时我们的猜想一定是正确的。故我们可以只在 $n\geq 6$ 的时候采用归纳的方法，$n < 6$ 时直接暴力枚举即可。

（当然，如果只推出 $n\geq 12$，也很容易在计算机的帮助下逐一验证 $n=3\sim 11$ 的情形，因而上面的推导不是必要的。）

---

下面我们将进入本文的重头戏：对取出的 $3$ 个人，证明一定可以将他们插到剩下 $n-3$ 个人的圆中的某个连续段，而不破坏排列的合法性。

注意到取出的三个人中有两个来自同一社团 $C$。观察到

观察 1 如果剩下 $n-3$ 人的排列中存在连续两个人来自 $C$，则可将 $3$ 人合法地插到这两个 $C$ 之间。

证明 如下图，把 $3$ 人中不在 $C$ 的那个人放在中间。注意到新出现的 可疑段 中，任何连续三个人中都有两个红色，那么如果同色必须同红色（否则两个红色的人又同在另一个社团里，这是非法的）。而显然没有三个连续的人都是红色的。（这里需要注意，由于原排列合法，因而两个 $C$ 外侧的两个人都不可能在社团 $C$。）

（这里 可疑段 指不能从原 $n-3$ 人的排列合法而直接推出合法的连续 $3$ 人，也就是至少包含 $1$ 个新人的连续段。）

---

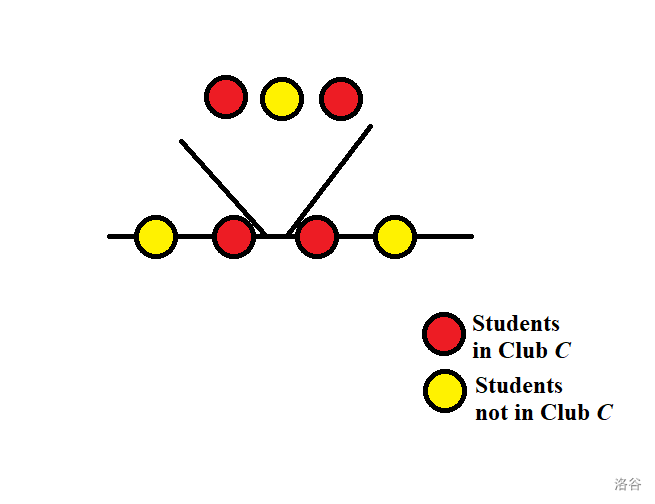
实际上，上面的证明中并没有用到 $C$ 的任何性质。我们完全可以换成一个别的社团。换言之

观察 2 如果 $3$ 人中有两个人同在某社团 $D$，而另外 $n-3$ 人的排列中存在两个相邻的人都在社团 $D$，那么可以将 $3$ 人合法地插进两个 $D$ 中间。

---

如果上面的做法还找不到合法解怎么办呢？我们对 $3$ 人之间的关系作一分类讨论。下面设 $P_0,P_1$ 是 $3$ 人中来自 $C$ 的两人，$P_2$ 是剩下的一人。

情况 A：$P_0,P_1$ 都不与 $P_2$ 有公共社团

由于 $C$ 是原本人数最多的社团，那么 $|C|\geq 3$，则剩下 $n-3$ 人中还有一人 $X$ 属于 $C$。我们在圆上找到他，设原本在他身后的两个人依次是 $Y,Z$，在他身前的人是 $W$。在他身后依次排列 $P_0,P_2,P_1$。分析所有可疑段，跨过 $P_2$ 的显然是合法的；由于 $X$ 两侧的人都不在 $C$ 中，则 $(W,X,P_0)$ 一定合法；唯一需要担心的是 $(P_1,Y,Z)$。但如果它不合法，说明三人在同一社团中，则 $P_0$ 不在这个社团中（否则 $P_0,P_1$ 就共同出现在两个社团中了）；我们把三个人的顺序变成 $P_1,P_2,P_0$ 即可。

情况 B：$P_0,P_1$ 中恰有一个人与 $P_2$ 有公共社团

不妨设 $P_0,P_2$ 共同在社团 $D$ 中。此时 $CD$ 地位是对称的。我们把环上所有在 $C,D$ 中至少一个的人涂成蓝色。（由于 $P_0$ 同时在 $CD$ 中，环上不可能有人同时在 $CD$ 中。）如果存在相邻的两个人一蓝一白，不妨设蓝色的人在社团 $C$ 中，仿照情况 A 的讨论知以下两种方案必有一种合法：

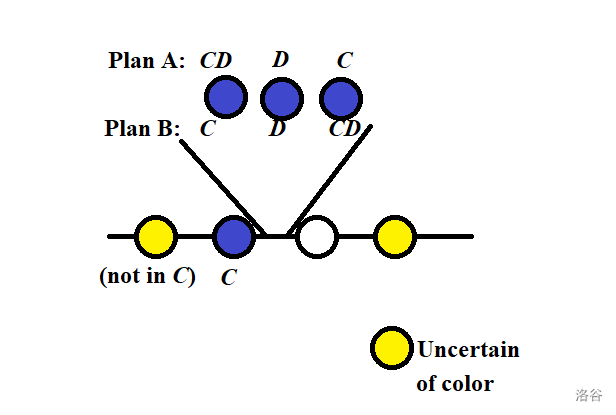
否则，环上的所有人颜色相同。而显见环上至少有一个蓝色，故环上全是蓝色。故环上一定是 $CDCD\cdots$ 间隔排列。下面的方案显然合法：

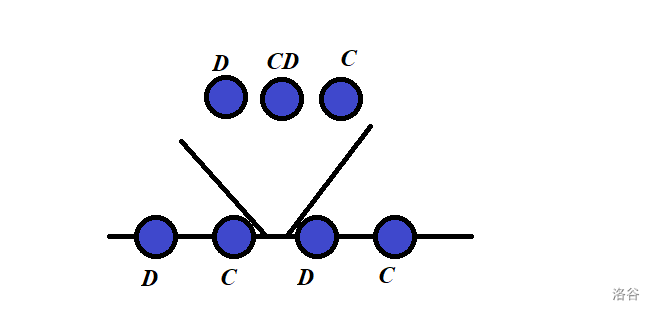
情况 C：$P_0,P_1$ 都与 $P_2$ 有公共社团

与情况 B 非常类似。不妨设 $P_0$ 参加社团 $CD$，$P_1$ 参加社团 $CE$，$P_2$ 参加社团 $CE$。同样把环上至少参加了 $CDE$ 一个社团的人涂成蓝色，并分类讨论是否存在 蓝-白 段。这里的讨论交给读者自行完成。

---

综上，我们证明了结论的正确性，并给出了一种实际的构造方法。

关于实现细节

哭哭……

上面的东西如果朴素实现的话时间复杂度 / 常数可能无法通过。但我们其实可以完全不理会证明的细节！我们只需要每次按上面的证明选人，然后暴力枚举这 $3$ 个人插在哪两个人之间以及他们的排列顺序如何；上面的证明保证了一定能找到解。

选人的时候如果用堆维护最大值的话会多一个 $\log$，但其实完全可以不用：用一个桶存下当前所有社团大小就可以了。时间复杂度可以做到 $O(n^2)$（这里认为 $m=O(n^2)$）。可以通过此题。