自动搬运

查看原文

来自洛谷，原作者为

	feecle6418 **

搬运于2025-08-24 22:45:08，当前版本为作者最后更新于2023-02-14 13:15:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这题要是想到“考虑右下边界”，就很容易了。可惜，想到这一点是很不容易也不”套路“的，至少我没想到。

然而，我们仍然能套路地，不需要任何思维火花地，解决本题。这也是本题解讲述的重点。

读完题，最让人迷惑的就是 $q$ 是 $p$ 的因数这个条件。所以，本题肯定要在这个条件上做文章。

接下来，我们考虑一些老生常谈的”思维技巧“，看能否套到这题上来。

• 主动强化题目条件，尝试增加条件让题目存在一个做法，尽管增加的条件可能相比原题太强了。要在 $n^2$ 个格子中找到一个作为答案，是很难的；但要是强制这个格子要么在上边界上要么在左边界上，则直接用线段树维护每行的格子数，线段树上二分即可（虽然维护的是行，但是对列二分也是容易的，因为列数随行数单调变化）。

  进一步，要是我们知道答案格的上边界所在行或是左边界所在列，也容易用线段树上二分找出答案。

  自然地，我们可以猜测：一定存在一种合法的答案，使得答案格要么在上边界上要么在左边界上。但可惜，这个猜想是错的，随便画个格子就可以举出反例。但这给了我们一点提示：我们能否将找寻答案的过程，完全放在一个固定的边界上进行呢？

• 从特殊情况考虑。诚然，本题中很难一眼看出什么有趣的特殊情况，不妨枚举所有”可能比较边界“的情况。因为上面提到要从 $q$ 是 $p$ 的因数入手，所以可以考虑一些较为特殊的因数。

  • 对于 $q=1,2,3$ 或者其它较小的正整数，似乎并不能给我们带来启示。
  • 对于 $q=p$，是平凡的。
  • 对于 $q=p/2$……似乎不是很平凡！

  这时就可以手搓一些小数据来找找性质了，如果不行的话再多试几个思维技巧。但是，要是你恰好刚刚已经想到了”主动强化题目条件“这个技巧，就不难发现或者猜测一个关键性质：如果 $q=p/2$，则可以强制答案格要么在上边界上要么在左边界上。读者可以感受一下这个猜测是很自然的：对于 $p$ 除了自身外最大的因数，要是以它为边界长度的生成格都只在内部，那这个题看起来就不怎么可做了。

• 从证明过程推出新的性质。我们来尝试着证明一下上面的猜想。事实上，证明是非常容易的。

  考虑一个楼梯，从下往上找到最上面一行 $i$，满足以这一行左端为生成格的子楼梯的边界长度 $\le p/2$。如果它恰好是 $p/2$，则证毕。否则它 $<p/2$，则其上一行左端为生成格的子楼梯边界长度 $>p/2$。考虑把 $(i,1)$ 生成的楼梯向右拓展（如下图红色线，编号为 1，的虚线部分），使得其长度达到恰好 $p/2$。注意，因为 $(i-1,1)$ 生成的楼梯边界长度至少为 $p/2+1$，所以这个位置向上一格一定在原楼梯内。假设这个拓展到的位置为 $(i,j)$，则 $(1,j)$ 一定合法（图中橙线，标号为 2），这是因为红线（包括虚线）和橙线的总长度是 $p$。

  

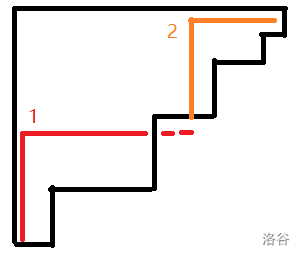
  这样，我们证明了上述性质。但是注意，全程用到的关于”$q=p/2$“的性质只有 $q+q=p$ 这一条！这意味着我们的讨论完全可以证明更宽泛的结论：

  • 最终结论：如果 $x+y=p$，则要么存在边界长度为 $x$ 的在左边界上的生成格，要么存在边界长度为 $y$ 的在上边界上的生成格。

综上，我们通过运用”思维技巧“，在每一步思考都有迹可循、没有让人大呼妙而摸不着头脑的步骤的前提下，发现了一个非常有趣的结论。

有了最终结论，本题就很容易了。设 $u=p/q$，则运用结论可以设计一个二分算法：我们每次要么找到一个边界长度为 $\lceil u/2\rceil\cdot q$ 的子楼梯，要么找到一个边界长度为 $\lfloor u/2\rfloor\cdot q$ 的子楼梯，递归 $O(\log V)$ 层后就找到了边界长度为 $q$ 的子楼梯。

上述过程都只需要维护每行的格子数和线段树上二分，而线段树的所有操作都是严格的，所以直接就可以可持久化。如果事先离散化，时间复杂度为 $O(m\log m\log V)$。