自动搬运

查看原文

来自洛谷，原作者为

	Infter 加训加训加训加训加训加训 ｜ 来自深渊的锐利 ｜ intp-a，不是很喜欢整天聊天但欢迎贴贴！

搬运于2025-08-24 22:44:50，当前版本为作者最后更新于2025-01-17 21:34:38，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

LibreOJ-3614 Luogu-P9040

很好的题。

---

先不考虑区间，先想 $l=1,r=n$ 的情况。

考虑 dp，$f_i$ 表示考虑 $[l,r]$ 的答案。

则容易得到：

$$f_i=\max\left\{f_{i-1}, f_{i-k}+s_i-s_{i-k}\right\},f_0=0 $$

其中 $s$ 为 $a$ 的前缀和。

这个转移本身是 $\Theta(n)$ 的。

遇见这种区间查询 DP 的通常都是动态 DP，但是由于下标跨了 $k$，矩阵的大小为 $\Theta(k)$，所以进行如此操作的时间复杂度为 $\Theta(k^3\log n)$，表现很差。

本题难点在此。

我们看到这个 DP 式子非常工整，灵光一现，唉我给她塞图上。

我们从 $u$ 向 $v$ 连长度为 $w$ 的边表示 $f_v$ 的转移方程式里有一项为 $f_u + w$。

突破口出现了！

原题所求的 $[l,r]$ 的答案就是 $l-1$ 到 $r$ 的最长路！（注意此处由于 $l$ 也要参与运算，所以起点为 $l-1$）

---

但是新的问题到来了，怎么给这样一个图求两点最短路呢？

显然不能 Johnson，这样比暴力还慢。

显然是要利用这个图的结构。

我们经过一顿梳理发现她长这样。

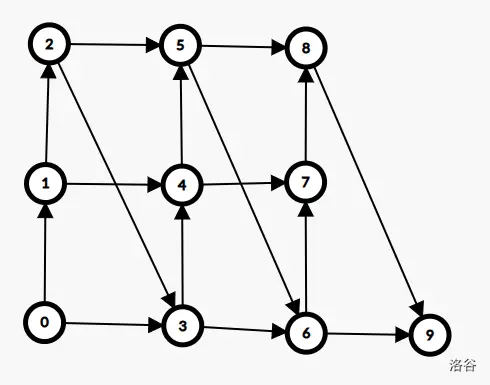
规规整整的跟个矩形一样。

知道网格求最短路的同学瞬间就懂了。

---

接下来是个很经典的 trick。

对于一类网格图，我们若要求若干点对间的最短或长路则采用以下算法：

我们考虑把询问离线下来分治。

每次分治面向原网格中的一个子网格。

为了方便我们设她是 $r\times c$ 的。

$1^\circ$ 若 $r>c$，我们按照中间行把她切成两半，对于中间行上每个点 $p$ 算出其对子矩阵里所有点的最短或长路。（若是 DAG 则可直接 DP），然后枚举所有被这个中间行分开的点对 $u,v$，将 $u$ 到 $v$ 的最短或长路经过 $p$ 松弛。（因为 $u$ 到 $v$ 的最短或长路一定经过 $p$）

$2^\circ$ 不然则按照中间列切，同样枚举中间列上的点来计算。

每次把切完的两个小网格分治下去，要把两端点都在。

每次分治 $O(n\sqrt n)$。

$$T(n)=O(n\sqrt n) + 2T(\cfrac{n}{2})$$

由主定理，总复杂度 $O(n\sqrt n)$。

---

回到这道题。

我们发现还有一些从最顶上指到底下的边，他们可以通过这条边而不需通过中间行。

对于这种情况我们可以额外枚举第一行的每个点，因为经过斜边一定要经过第一行的点。

但是有可能在同一侧的节点的最长路穿下去再慢慢爬上来的情况。

这种情况我们也要给在同一侧的点对统计答案，但是由于只有一次不影响复杂度。

#include <bits/stdc++.h>
using namespace std;

#define int long long
#define endl '\n'
#define debug(x) cerr << #x << " = " << x << endl
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define per(i, a, b) for (int i = (a); i >= (b); i--)
#define gn(u, v) for (int v : G.G[u])
#define pb emplace_back
#define mp make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define pii pair<int, int>
#define vi vector<int>
#define vpii vector<pii>
#define vvi vector<vi>
#define no cout << "NO" << endl
#define yes cout << "YES" << endl
#define all(x) x.begin(), x.end()
#define rall(x) x.rbegin(), x.rend()
#define tomin(x, y) ((x) = min((x), (y)))
#define tomax(x, y) ((x) = max((x), (y)))
#define ck(mask, i) (((mask) >> (i)) & 1)
#define pq priority_queue
#define FLG (cerr << "Alive!" << endl);

constexpr int MAXN = 6e5 + 5;
constexpr int INF = 0x3f3f3f3f3f3f3f3f;
int n, k, q;
int a[MAXN];
vector<vpii> G;
vector<vpii> H;

struct Query {
    int u, v, ans;
};
vector<Query> query;

vi num[MAXN];
int x[MAXN], y[MAXN];
int dis[2][MAXN];

void get(int start, const vector<vpii>& G, const vector<vpii>& H, int lx, int rx, int ly, int ry, bool typ) {
    queue<int> q;
    q.push(start);
    dis[typ][start] = -1;
    vi vis;
    vis.pb(start);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (auto [v, w] : G[u]) {
            // cerr << "!" << v << endl;
            if (x[v] < lx || x[v] > rx || y[v] < ly || y[v] > ry)
                continue;
            if (dis[typ][v] != -1) {
                dis[typ][v] = -1;
                q.push(v);
                vis.pb(v);
            }
        }
    }

    rep (i, lx, rx) {
        rep (j, ly, ry) {
            dis[typ][num[i][j]] = -INF;
        }
    }

    if (typ)
        sort(all(vis), greater<>());
    else
        sort(all(vis));
    dis[typ][start] = 0;
    for (int u : vis) {
        if (u == start)
            continue;
        dis[typ][u] = -INF;
        for (auto [v, w] : H[u]) {
            if (x[v] < lx || x[v] > rx || y[v] < ly || y[v] > ry)
                continue;
            // cerr << v << " " << w << endl;
            tomax(dis[typ][u], dis[typ][v] + w);
        }
        // cerr << "dis from " << start << " to " << u << " with type " << typ << " is " << dis[typ][u] << endl;
    }
}

void solve(int lx, int rx, int ly, int ry, vector<Query>& q) {
    if (lx > rx || ly > ry || q.empty())
        return;
    rep (i, lx, rx) {
        rep (j, ly, ry) {
            dis[false][num[i][j]] = dis[true][num[i][j]] = 0;
        }
    }
    if (rx - lx <= ry - ly) {
        int mid = ly + ry >> 1;

        vector<Query> l, r, now;
        for (auto [u, v, ans] : q) {
            if (y[u] < mid && y[v] < mid) {
                l.pb(Query{u, v, ans});
            } else if (y[u] > mid && y[v] > mid) {
                r.pb(Query{u, v, ans});
            } else {
                now.pb(Query{u, v, ans});
            }
        }

        rep (tmp, lx, rx) {
            int cur = num[tmp][mid];
            get(cur, G, H, lx, rx, ly, ry, false);
            get(cur, H, G, lx, rx, ly, ry, true);
            for (auto& [u, v, ans] : now) {
                // if (u == 170 && v == 200) {
                //     cerr << lx << " " << rx << " " << ly << " " << ry << endl;
                //     cerr << dis[0][u] + dis[1][v] << " " << dis[1][u] + dis[0][v] << endl;
                // }
                tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
                // cerr << dis[0][u] << " " << dis[1][u] << " " << dis[0][v] << " " << dis[1][v] << endl;
            }
            for (auto& [u, v, ans] : l) {
                // if (u == 170 && v == 200) {
                //     cerr << lx << " " << rx << " " << ly << " " << ry << endl;
                //     cerr << dis[0][u] + dis[1][v] << " " << dis[1][u] + dis[0][v] << endl;
                // }
                tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
                // cerr << dis[0][u] << " " << dis[1][u] << " " << dis[0][v] << " " << dis[1][v] << endl;
            }
            for (auto& [u, v, ans] : r) {
                // if (u == 170 && v == 200) {
                //     cerr << lx << " " << rx << " " << ly << " " << ry << endl;
                //     cerr << dis[0][u] + dis[1][v] << " " << dis[1][u] + dis[0][v] << endl;
                // }
                tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
                // cerr << dis[0][u] << " " << dis[1][u] << " " << dis[0][v] << " " << dis[1][v] << endl;
            }
        }

        solve(lx, rx, ly, mid - 1, l);
        solve(lx, rx, mid + 1, ry, r);

        int i = 0, j = 0, cnt = 0;
        for (auto& [u, v, ans] : q) {
            if (y[u] < mid && y[v] < mid) {
                ans = l[i++].ans;
            } else if (y[u] > mid && y[v] > mid) {
                ans = r[j++].ans;
            } else {
                ans = now[cnt++].ans;
            }
        }
    } else {
        int mid = lx + rx >> 1;

        vector<Query> l, r, now;
        for (auto [u, v, ans] : q) {
            if (x[u] < mid && x[v] < mid) {
                l.pb(Query{u, v, ans});
            } else if (x[u] > mid && x[v] > mid) {
                r.pb(Query{u, v, ans});
            } else {
                now.pb(Query{u, v, ans});
            }
        }

        rep (tmp, ly, ry) {
            int cur = num[mid][tmp];
            get(cur, G, H, lx, rx, ly, ry, false);
            get(cur, H, G, lx, rx, ly, ry, true);
            for (auto& [u, v, ans] : now) {
                tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
            }
            for (auto& [u, v, ans] : l) {
                tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
            }
            for (auto& [u, v, ans] : r) {
                tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
            }
        }

        // if (lx == 1 && rx == k) {
            rep (tmp, ly, ry) {
                int cur = num[lx][tmp];
                get(cur, G, H, lx, rx, ly, ry, false);
                get(cur, H, G, lx, rx, ly, ry, true);
                for (auto& [u, v, ans] : now) {
                    tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
                }
                for (auto& [u, v, ans] : l) {
                    tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
                }
                for (auto& [u, v, ans] : r) {
                    tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));
                }
            }
        // }

        solve(lx, mid - 1, ly, ry, l);
        solve(mid + 1, rx, ly, ry, r);

        int i = 0, j = 0, cnt = 0;
        for (auto& [u, v, ans] : q) {
            if (x[u] < mid && x[v] < mid) {
                ans = l[i++].ans;
            } else if (x[u] > mid && x[v] > mid) {
                ans = r[j++].ans;
            } else {
                ans = now[cnt++].ans;
            }
        }
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n >> k >> q;
    int tmp = (n / k + 1) * k - 1;
    rep (i, 1, n)
        cin >> a[i];
    rep (i, 1, tmp)
        a[i] += a[i - 1];
    
    G.resize(tmp + 1);
    H.resize(tmp + 1);
    rep (i, 1, tmp) {
        G[i - 1].pb(mp(i, 0));
        H[i].pb(mp(i - 1, 0));
        if (i >= k)
            G[i - k].pb(mp(i, a[i] - a[i - k])),
            H[i].pb(mp(i - k, a[i] - a[i - k]));
    }
    query.resize(q);
    rep (i, 0, q - 1) {
        cin >> query[i].u >> query[i].v;
        query[i].u--;
        query[i].ans = 0;
    }

    rep (i, 1, k) {
        num[i].resize(n / k + 2);
    }
    rep (i, 0, (n / k + 1) * k - 1) {
        num[i % k + 1][i / k + 1] = i;
        x[i] = i % k + 1;
        y[i] = i / k + 1;
    }
    // rep (i, 0, n) {
    //     for (auto [v, w] : G[i]) {
    //         cerr << i << " " << v << " " << w << endl;
    //     }
    // }

    solve(1, k, 1, n / k + 1, query);
    // cerr << x[170] << " " << y[170] << " " << x[200] << " " << y[200] << endl;

    rep (i, 0, q - 1)
        cout << query[i].ans << endl;

    return 0;
}