自动搬运

查看原文

来自洛谷，原作者为

	Ecrade_ 算法竞赛打 APIO，就像，只能度过一个相对失败的人生。

搬运于2025-08-24 22:44:40，当前版本为作者最后更新于2023-01-31 06:10:59，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题意：

• 给定一棵有 $n$ 个结点的树，$1$ 为根结点，初始时每个结点均为白色。
• 你可以改变任意一个结点的颜色（即白变黑，黑变白），称为一次操作。
• 当某个结点子树内的所有结点均为黑色且其余结点均为白色时，标记这个结点。
• 求使每个结点均被标记过且最终均为白色的最少操作次数。
• $2\le n\le 2\cdot10^5$。

---

下文中 “ 清空状态 ” 表示每个结点均为白色的状态，记 $sz_u$ 表示结点 $u$ 的子树大小，$fa_u$ 表示结点 $u$ 的父结点，$son_u$ 表示结点 $u$ 的子结点所组成的集合，$\text{lca}(u,v)$ 表示结点 $u,v$ 的最近公共祖先。

假如当前结点 $u$ 满足了可被标记的状态，那么我们下一步可以干什么？容易发现只有如下三种决策：

1. 进行 $2\cdot sz_u$ 次操作直接变为清空状态；
2. 进行 $2\cdot (sz_{fa_u}-sz_u)$ 次操作去标记 $fa_u$；
3. 进行 $2\cdot (sz_u-sz_v)$ 次操作去标记 $v$，其中 $v\in son_u$。

所以，存在某个结点可被标记的状态才是我们应当去关注的状态，且如何达成该状态的中间过程完全可以略去。

考虑将操作分段。具体地，对于每段操作，初始时以及经过这段操作之后均为清空状态，但中途不允许出现清空状态。可以发现，每段操作相互独立，那么我们接下来着重考察一段操作的性质。

根据定义，中途不允许出现清空状态，所以操作过程中仅能出现上文中的后两种决策，也就是依次标记一条树上路径的所有结点。注意，这条路径是任意的，它可以不是简单路径，也就是说，这条路径可以重复经过同一个结点任意多次。但是由于其任意性，这种路径的贡献很难直接计算出来，而且覆盖结点所形成的集合也难以描述。进而我们考虑，能否对路径加一些限制，使其变得不那么 “ 任意 ” ？

答案是可以的。选取两个叶子结点 $u,v$（$u,v$ 可以相同），再选取 $\text{lca}(u,v)$ 或其某个祖先结点 $w$，则我们可以将所有路径的形态都归为一类：依次标记 $u\to w$ 简单路径上的所有结点，再依次标记 $w\to v$ 简单路径上的所有结点。换句话来说，我们总是先进行若干次第二种决策，再进行若干次第三种决策。 不难通过计算得到，这样需要的操作次数恰好为 $2\cdot sz_w$。

对路径形态给出一个不怎么严谨的证明，大家意会下即可。假如出现了如下图所示的情形（一条黑边上可能有多个结点）：

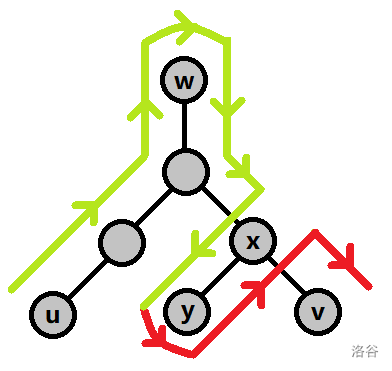
这种情况下需要的操作次数为 $2\cdot (sz_w+sz_x)-sz_y$。而我们完全可以如下图所示将其分为两条满足条件的路径：

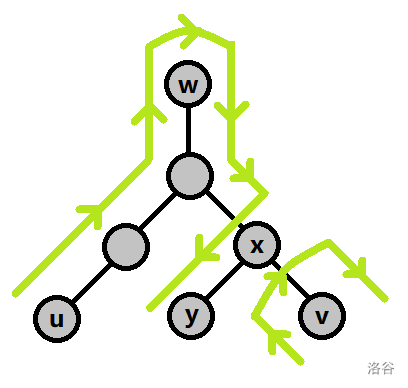
假设 $x$ 的在 $x$ 到 $v$ 路径上的子结点为 $z$，那么这种情况下需要的操作次数为 $2\cdot (sz_w+sz_z)<2\cdot (sz_w+sz_x-sz_y)<2\cdot (sz_w+sz_x)-sz_y$，严格优于原先的路径。

那么题目可以转化为：用若干条如上形态的路径覆盖所有结点，每条路径所需的操作次数为，路径上深度最小的结点的子树大小的两倍。

很自然地考虑使用树形 DP 求解。令 $f_{u,0}$ 表示覆盖结点 $u$ 子树内所有结点所需的最少操作次数，$f_{u,1}$ 表示有且仅有一条从结点 $u$ 到其子树内某个叶结点的链，其上的所有结点均未被覆盖，而结点 $u$ 子树内其余结点均被覆盖所需的最少操作次数。

转移方程为：

$$\begin{cases}f_{u,0}=\min\left(2\cdot (sz_u-\max\limits_{v\in son_u}\left\{sz_v\right\})+\sum\limits_{v\in son_u}{f_{v,0}},\ 2\cdot sz_u+\min\limits_{v_1,v_2\in son_u,v_1\neq v_2}\left\{f_{v_1,1}+f_{v_2,1}+\sum\limits_{v\in son_u,v\neq v_1,v\neq v_2}{f_{v,0}}\right\}\right)\\f_{u,1}=\min\limits_{v\in son_u}\left\{f_{v,1}+\sum\limits_{v'\in son_u,v'\neq v}{f_{v',0}}\right\}\end{cases} $$

$f_{u,1}$ 的转移方程比较好理解，就是 $u$ 与某个子结点 $v$ 中未被覆盖的链合并成一条新的未被覆盖的链，其余子结点的子树均被完全覆盖。

$f_{u,0}$ 的转移需分为两种情况考虑，第一种情况是假设 $u$ 的所有子结点的子树均被完全覆盖，那么我们就需要选择 $u$ 的某个子结点 $v$，将 $v$ 中覆盖 $v$ 的路径拉长一截来覆盖 $u$，原本路径上深度最小的结点为 $v$，而现在路径上深度最小的结点变为了 $u$，那么这条路径的操作次数也就相应地增加了 $2\cdot (sz_u-sz_v)$；第二种情况是将 $u$ 与其某两个子结点 $v_1,v_2$ 中的两条未被覆盖的链合并成一条操作次数为 $2\cdot sz_u$ 的路径，其余子结点的子树均被完全覆盖。

实现时记录 $f_{v,0}$ 的和、$f_{v,1}-f_{v,0}$ 的最小值及次小值、以及 $sz_v$ 的最大值即可。

至此，我们便用 $O(n)$ 的时间复杂度解决了本题。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,x,tot,hd[200009],sz[200009],f[200009][2];
struct st{ll x,y;}eg[400009];
void addedge(ll u,ll v){eg[++ tot] = (st){v,hd[u]},hd[u] = tot;}
inline ll read(){
	ll s = 0,w = 1;
	char ch = getchar();
	while (ch > '9' || ch < '0'){ if (ch == '-') w = -1; ch = getchar();}
	while (ch <= '9' && ch >= '0') s = (s << 1) + (s << 3) + (ch ^ 48),ch = getchar();
	return s * w;
}
void dfs(ll u,ll fa){
	sz[u] = 1;
	ll sum = 0,mx = 0,mn = 1e18,mn2 = 1e18;
	for (ll i = hd[u];i;i = eg[i].y){
		ll v = eg[i].x;
		if (v == fa) continue;
		dfs(v,u),sum += f[v][0],mx = max(mx,sz[v]),sz[u] += sz[v];
		ll qwq = f[v][1] - f[v][0];
		if (qwq <= mn) mn2 = mn,mn = qwq;
		else mn2 = min(mn2,qwq);
	}
	if (sz[u] == 1){f[u][0] = 2; return;}
	f[u][0] = 2 * sz[u] + sum,f[u][1] = sum + mn;
	if (mn2 < 1e18) f[u][0] += mn + mn2;
	f[u][0] = min(f[u][0],sum + 2 * (sz[u] - mx));
}
int main(){
	n = read();
	for (ll i = 2;i <= n;i += 1) x = read(),addedge(x,i),addedge(i,x);
	dfs(1,0),printf("%lld",f[1][0]);
	return 0;
}