自动搬运

查看原文

来自洛谷，原作者为

	泥土笨笨 《算法竞赛实战笔记》作者

搬运于2025-08-24 22:44:34，当前版本为作者最后更新于2023-02-10 22:03:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

此题细节非常多，比赛的时候给我错的死去活来的，还好数据不强。应该也是因为不好造数据吧。

关于其他题解的错误

看了一下其他题解，感觉有一些地方可以商榷。没有兴趣的同学可以跳过这一部分。

针对 @zac2010 的题解中的代码，给出一组 hack 数据。

1
DFB
FDD

这组数据答案应该是 $3$，首先把 F 变成 B，原始字符串变成 DBB。第二步把 D 变成 F，原始字符串变成 FBB，第三步把 B 变成 D，得到答案。由此可见答案为 $3$，但是题解中的代码跑出来答案是 $4$。

针对 @Demeanor_Roy 题解中的思路：

若借助字符串中不存在的点或者已经变换完成的联通块中入度为 $0$ 的点，答案增加 $1$。

这里其实有问题，不能借助已经完成的连通块中入度 $0$ 的点进行变换，因为这个点已经变换成了它想要的字符。如果还借助它，就会导致一个点要变成两种不同的字符。

解题思路

首先判断无解的情况，显然第一种无解是一个字母要变换成两个或者两个以上不同的字母。这个相信大家可以轻松实现。

第二种无解的情况是，t 字符串中出现了所有的字母，但是 s 字符串和 t 字符串不相同。原因一会儿会详细解释，读者有兴趣可以在这里先思考一下。

在没有第一种无解情况的情况下，我们把这个问题转换成一个图论问题。对于 $s$ 中某个字母 $s_i$ 要变成 $t$ 中另一个字母 $t_i$，就从 $s_i$ 到 $t_i$ 之间连一条有向边。这样我们得到一张最多 $52$ 个点的有向图。重边和自环都不建边。对于这种每个点最多有一条出边的图，大概会分为三种情况：链，带有入度的环，纯环。如图：

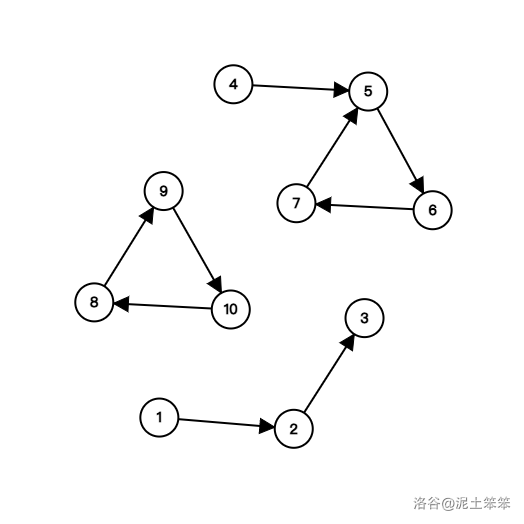
第一种情况，图中 $1$ 到 $2$，$2$ 到 $3$ 这种链。链是很好处理的，答案的数量等于边的条数。

第二种情况，带有入度的链，比如图上 $4$ 到 $7$ 这四个点。虽然环不能直接操作，但是可以在环有入度的位置，把环断开。先把 $7$ 变成 $4$，再把 $6$ 变成 $7$，再把 $5$ 变成 $6$，再把 $4$ 变成 $5$。这样也可以处理，答案的数量等于边的条数。

第三种情况，纯环，图中 $8$ 到 $10$ 这三个点。这三个点如果要解开，需要额外借一个点进来，花 $4$ 步才能处理。所以如果存在这样的纯环，每个纯环的答案等于边的条数加 $1$。

经过刚才的分析，我们发现答案等于边的条数加上纯环的个数。不过这里还有一个特殊情况，刚才说到纯环需要借一个点来拆环，这个点必须是没有在 $t$ 里面出现过的，否则有别的字符要变成它，又要从环里拆一个点变成它，一会儿从它变回环里的点的时候，就会出现一对多的情况。

这时候我们可以解释前文提到的第二种无解情况了。如果所有字符都在 $t$ 中出现过，除非 $s$ 和 $t$ 完全相等，否则无解。

首先因为每个字符只能变换成一种字符，而不会变换成两种以上的字符。（否则在前面情况一已经判掉了）那么 $s$ 中字符的种类数一定大于等于 $t$ 中字符的种类数。而 $t$ 中已经有所有的字母了，那么 $s$ 中一定有所有的字母。既然如此，也就不会出现 $s$ 中某两种字符变成 $t$ 中相同字符的情况。也就是说，$s$ 中字符和 $t$ 中字符构成一对一的映射关系。那么要么就是每个字母变成自己，要么就是形成一个纯环。但是只要出现纯环就解不开，因为已经没有别的点可以借用了。所以必须 $s$ 和 $t$ 完全相等才行。

思路清楚，代码实现就很简单啦。

#include <iostream>
#include <cstring>
#include <set>
#include <queue>

using namespace std;
typedef long long ll;
const ll MAXN = 1e5 + 5;
const ll MOD = 1e9 + 7;

int T, n, to[300];//to表示i要变成什么
int in[300];//每个字符的入度
int vis[300];//vis数组记录每个字母是否已经能成功变化到它想去的字母
char s[MAXN], t[MAXN];

//从入度为0的点出发，把能到的点都标记vis
void topo() {
    queue<int> q;
    for (int i = 'A'; i <= 'Z'; ++i) {
        if (in[i] == 0) {
            q.push(i);
        }
    }
    for (int i = 'a'; i <= 'z'; ++i) {
        if (in[i] == 0) {
            q.push(i);
        }
    }
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        vis[u] = 1;
        int v = to[u];
        if (vis[v] == 0) {
            in[v] = 0;//只要能从不在环上的点走过来，强制进队
            q.push(v);
        }
    }
}

//把从u出发同一个环上的点都标记一遍
void dfs(int u) {
    vis[u] = 1;
    int v = to[u];
    if (vis[v] == 0) dfs(v);
}

int main() {
    cin >> T;
    while (T--) {
        set<char> b;//集合记录所有在s中出现过的字母
        memset(to, 0, sizeof to);
        memset(in, 0, sizeof in);
        memset(vis, 0, sizeof vis);
        cin >> s >> t;
        n = ::strlen(s);
        //第一种无解的情况，一个字符要变成两种以上不同字符，肯定不行
        int good = 1;
        for (int i = 0; i < n; ++i) {
            if (to[s[i]] == 0 || to[s[i]] == t[i]) {
                to[s[i]] = t[i];
            } else {
                good = 0;
            }
            b.insert(t[i]);
        }
        if (!good) {
            cout << -1 << endl;
            continue;
        }
        //第二种无解的情况，如果所有字母都在t中出现过，那么s和t必须相等才行。
        if (b.size() == 52) {
            if (strcmp(s, t) == 0) {
                cout << 0 << endl;
            } else {
                cout << -1 << endl;
            }
            continue;
        }
        //把每个原始字母向结果字母连边，建一张有向图，自环不管
        memset(to, 0, sizeof to);
        int ans = 0;//统计边的条数，其实就是需要的变化的数量
        for (int i = 0; i < n; ++i) {
            if (to[s[i]] == 0 && s[i] != t[i]) {
                to[s[i]] = t[i];
                in[t[i]]++;
                ans++;
            }
        }
        topo();
        //此时一定有解，对于现在还没标记的点，一定是在一个纯环里面，此时对于每个环答案加1
        for (int i = 'a'; i <= 'z'; ++i) {
            if (vis[i] == 0) {
                ans++;
                dfs(i);
            }
        }
        for (int i = 'A'; i <= 'Z'; ++i) {
            if (vis[i] == 0) {
                ans++;
                dfs(i);
            }
        }
        cout << ans << endl;
    }
    return 0;
}