[北大集训 2021] 经典游戏

0
15011418730 LV 7 @ 2025-8-24 22:44:25
自动搬运

查看原文

来自洛谷，原作者为

Licykoc
红雨漂泊泛起了回忆怎么潜

搬运于2025-08-24 22:44:25，当前版本为作者最后更新于2023-06-08 22:32:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

先考虑没有特殊能力的情况。容易发现点 $u$ 的 SG 值为 $u$ 到 $u$ 子树内的最大距离，设其为 $f_u$ 。那么整个游戏的 SG 值就是 $\bigoplus _u{[a_u \bmod 2=1]f_u}$ ，设其为 $S$ 。

进而得出，额外放置一枚棋子后先手仍然必胜的充要条件是 $\max\{f_u\} \lt S$ 。若不满足，则一定存在某个 $f_u = S$ ，那么只要在点 $u$ 放置一枚棋子 $S$ 就变成 $0$ 了，先手必败。

于是，原问题转化为：

给定一颗树，每个点有黑白两种颜色， $u$ 点权值 $f_u$ 为 $u$ 到 $u$ 子树内的最大距离，记 $S$ 为所有黑点权值异或和。每次操作给定 $x,y$ ，先翻转点 $x$ 的颜色，再询问有多少个点满足：与点 $y$ 相邻（包括点 $y$ ）且以该点为根时 $\max\{f_u\} \lt S$ 。

这里给出一种与其他两篇题解不同的维护方法。

基本思路是对每个点都维护以它为根时的 $\max\{f_u\}$ 和 $S$ ，记为 $mx_u$ 和 $S_u$ 。

首先一遍树形 dp 算出初始时的 $mx_u$ 和 $S_u$ ，实现时注意 $mx_u$ 事实上就等于 $u$ 到 $u$ 子树内的最大距离。

考虑修改，假设现在翻转点 $u$ ，设 $mx_u$ 经过 $(u,v)$ 这条边，切断 $(u,v)$ （并不是真的切断，只是为了方便理解）。对于与 $u$ 连通的点 $x$ ，翻转点 $u$ 对 $S_x$ 的贡献就是异或上 $mx_u$ 。而对于与点 $v$ 连通的点 $y$ ，贡献则是异或上 $u$ 到与 $u$ 连通的点的最大距离。因为树的形态不变，所以这个可以在之前树形 dp 时预处理出来。将树以 dfs 序拍平，则上述操作可以归纳为区间异或，数据结构可以轻松维护。

再来看查询，假设查询点 $u$ 。先把 $u$ 点父亲和点 $u$ 暴力判掉，接下来考虑点 $u$ 的儿子。这相当于查询：
$\sum_{v\in son_u}[mx_v \lt S_v]$
$mx_v$ 显然始终不会变，但是 $S_v$ 是在动态改变的。所以我们的目标上将 $S_v$ 以某个不变量或者易于维护的量来替代掉。观察之前的修改操作，可以将 $S_v$ 改写为 $S'_v \oplus P_v$ ，其中 $S'_v$ 表示初始时的 $S_v$ ， $P_v$ 则表示 $S_v$ 应异或上的值。发现 $S'_v$ 始终不变。但是 $P_v$ 却会改变，似乎毫无进展？

并不是，若对原树进行长剖，那么在修改的时候点 $v$ 要么是点 $u$ 的长儿子要么是 $u$ 点父亲，只有 $O(1)$ 种可能！这意味这点 $u$ 除去长儿子那棵子树，其他子树内的点 $x$ 应异或的值都相同，也就是那些 $P_x$ 均等于 $x$ 父亲的 $P$ 值！同理，对于 $u$ 点父亲那部分，也同样遵循上述规则。

那么查询时先暴力判断点 $u$ 的长儿子，剩余部分的查询即为：
$$\sum_{v\in son_u \setminus \{hson_u\}}[mx_v \lt S'_v \oplus P_u] $$
因为剩余部分均为轻儿子，那么 $mx_v$ 都等于 $mx_u+1$ ，所以查询即为：
$$\sum_{v\in son_u \setminus \{hson_u\}}[mx_u+1 \lt S'_v \oplus P_u] $$
其中 $mx_u, S'_v$ 均为不变量， $P_u$ 仅跟 $u$ 点有关，使用 trie 树轻松维护。

这就做完了？并没有，上面的分析是有漏洞的，考虑这样一张图：

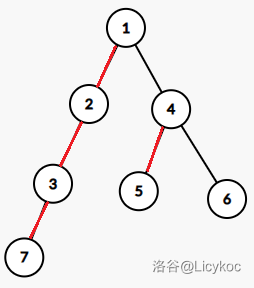
红边为重边，当前修改点 $4$ ，那么会切断 $(4, 1)$ 这条边，根据上面的分析， $P_4$ 应等于 $P_1$ ，但实际上却并不相等（ $P_4=4, P_1=1$ ）。但是这种错误只会发生在点 $4$ 这一个点上，所以我们将它暴力修改成正确的即可。

总时空复杂度： $O((n+q)\log n)$ 。

参考实现：
```
#include <bits/stdc++.h>

constexpr int N = 2e7;

class trie {
private:
  int ch[2][N], tot = 0, siz[N];
  std::vector<int> root;

  void modify(int &u, int x, int dep, int v) {
    if (u == 0) {
      u = ++tot;
    }

    siz[u] += v;

    if (dep < 0) {
      return;
    }

    int p = x >> dep & 1;
    modify(ch[p][u], x, dep - 1, v);
  }

  int query(int u, int v, int x, int dep) {
    if (u == 0) {
      return 0;
    }

    if (dep < 0) {
      return siz[u];
    }

    int pv = v >> dep & 1, px = x >> dep & 1;
    return query(ch[px ^ pv][u], v, x, dep - 1) + (px == 0 ? siz[ch[pv ^ 1][u]] : 0);
  }

public:
  trie(int n) : root(n + 1) {}

  void insert(int i, int x) {
    modify(root[i], x, 30, 1);
  }

  void erase(int i, int x) {
    modify(root[i], x, 30, -1);
  }

  int query(int i, int v, int x) {
    return query(root[i], v, x, 30);
  }
};

template<typename T>
class fenwick {
private:
  int n;
  std::vector<T> tr;

public:
  fenwick() = default;
  fenwick(int N) : n(N + 5), tr(N + 6, 0) {}

  void add(int x, T y) {
    ++x;
    for (int i = x; i <= n; i += i & -i) {
      tr[i] ^= y;
    }
  }

  void add(int l, int r, int x) {
    if (l > r) {
      return;
    }

    add(l, x);
    add(r + 1, x);
  }
  
  T qry(int x) {
    ++x;
    T res = 0;
    for (int i = x; i > 0; i -= i & -i) {
      res ^= tr[i];
    }
    return res;
  }
};

signed main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(nullptr);

  int n, m;
  std::cin >> n >> n >> m;

  std::vector<std::vector<int>> adj(n + 1);

  for (int i = 1; i < n; ++i) {
    int x, y;
    std::cin >> x >> y;
    adj[x].emplace_back(y);
    adj[y].emplace_back(x);
  }

  std::vector<int> a(n + 1);

  for (int i = 1; i <= n; ++i) {
    std::cin >> a[i];
    a[i] &= 1;
  }

  std::vector<int> max(n + 1), sec(n + 1), to(n + 1), hson(n + 1);
  std::vector<int> par(n + 1), dfn(n + 1), siz(n + 1);
  std::vector<int> S(n + 1);
  int timer = 0;

  auto dfs = [&](auto &self, int u, int fa) -> void {
    if (fa > 0) {
      adj[u].erase(std::find(adj[u].begin(), adj[u].end(), fa));
    }

    dfn[u] = ++timer;
    par[u] = fa;
    siz[u] = 1;

    for (auto v : adj[u]) {
      self(self, v, u);

      if (hson[u] == 0 || max[v] > max[hson[u]]) {
        hson[u] = v;
      }

      if (max[v] + 1 > max[u]) {
        sec[u] = max[u];
        max[u] = max[v] + 1;
      } else {
        sec[u] = std::max(sec[u], max[v] + 1);
      }

      siz[u] += siz[v];
    }

    to[u] = hson[u];

    if (a[u] > 0) {
      S[1] ^= max[u];
    }
  };
  dfs(dfs, 1, 0);

  auto dfs1 = [&](auto &self, int u) -> void {
    for (auto v : adj[u]) {
      int w = to[u] == v ? sec[u] : max[u];

      if (w + 1 > max[v]) {
        sec[v] = max[v];
        max[v] = w + 1;
        to[v] = u;
      } else {
        sec[v] = std::max(sec[v], w + 1);
      }

      w = S[u];
      w ^= a[u] > 0 && to[u] == v ? max[u] ^ sec[u] : 0;
      w ^= a[v] > 0 && to[v] == u ? sec[v] ^ max[v] : 0;
      S[v] = w;

      self(self, v);
    }
  };
  dfs1(dfs1, 1);

  trie T(n);
  fenwick<int> seg(n);
  auto pre = S;

  for (int u = 1; u <= n; ++u) {
    for (int v : adj[u]) {
      if (v != hson[u]) {
        T.insert(u, S[v]);
      }
    }
  }

  auto flip = [&](int u) {
    auto subtree_modify = [&](int u, int v, int w) {
      seg.add(dfn[u], dfn[u] + siz[u] - 1, v);
      seg.add(1, dfn[u] - 1, w);
      seg.add(dfn[u] + siz[u], n, w);
    };

    if (to[u] == par[u]) {
      if (hson[par[u]] != u) {
        T.erase(par[u], pre[u]);
        pre[u] ^= max[u] ^ sec[u];
        T.insert(par[u], pre[u]);
      }

      subtree_modify(u, max[u], sec[u]);
    } else {
      assert(to[u] == hson[u]);
      subtree_modify(to[u], sec[u], max[u]);
    }

    a[u] ^= 1;
  };

  auto query = [&](int u) {
    auto check = [&](int u) {
      if (u < 1) {
        return false;
      }

      return (S[u] ^ seg.qry(dfn[u])) > max[u];
    };

    int res = check(u) + check(hson[u]) + check(par[u]);
    return res + T.query(u, seg.qry(dfn[u]), max[u] + 2);
  };

  while (m--) {
    int x, y;
    std::cin >> x >> y;
    flip(x);
    std::cout << query(y) << '\n';
  }
}
```