自动搬运

查看原文

来自洛谷，原作者为

	AC_CSP AFO.

搬运于2025-08-24 22:44:12，当前版本为作者最后更新于2022-12-26 14:46:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

$\text{Part 1}$

首先考虑暴力。预处理每个点之间的距离，然后枚举每个点的三种状态，最后进行判断。这样的时间复杂度是 $\mathcal{O}(n3^n)$。期望得分 $7\text{pts}$。

$\text{Part 2}$

接着，很容易发现这是一个树形 $\text{DP}$。为了方便我们把它看成一棵有根树。而由于一个点选什么对它的 $r$ 级祖先都是有贡献的，同时 $1\le r\le 7$，所以我们可以考虑加上一个状压 $\text{DP}$。

不妨设 $f(i,S,T)$ 表示以 $i$ 为根的子树有 $S$ 集合的贡献，需要 $T$ 集合的贡献的最小价值。其中 $S,T$ 是两个 $r$ 位二进制数。

我们对当前节点的 $S,T$ 进行枚举，再对当前儿子的 $S,T$ 进行枚举，最后合并为新的 $S,T$。

图中是 $r=3$ 的情况。其中 $x,y$ 表示 $u$ 节点的 $S,T$，$z,w$ 表示 $v$ 节点的 $S,T$，$s,t$ 表示合并出来的 $S,T$。

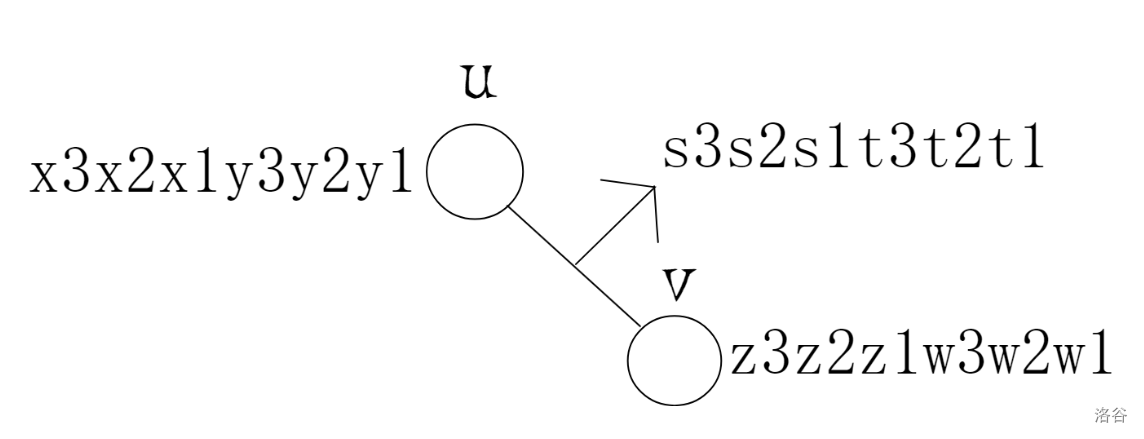
我们发现，在合并过程中，$v$ 的状态会发生错位现象，所以我们要进行分类讨论。

于是我们可以得到下表：

上文中红色的状态是不必要或不合法的。

时间复杂度 $\mathcal{O}(n16^r)$，期望得分 $43\text{pts}$。

如果特判 $r=1$ 的情况，进行 $\mathcal{O}(n)$ 的 $\text{DP}$，可以拿到 $49\text{pts}$。

$\text{Part 3}$

考虑进行优化。我们现在是枚举两个状态合并为一个状态，不妨枚举一个状态拆为两个状态。这样我们就可以进行预处理。

于是得到下表：

不妨枚举所有的可能性，这样的复杂度是 $\mathcal{O}(n8^r)$ 的，期望得分 $81\text{pts}$。

$\text{Part 4}$

继续进行优化。我们发现 $01$ 的限制比 $00$ 更加严格，因此将状态合并。

优化前：

优化后：

这样的时间复杂度是 $\mathcal{O}(n7^r)$，期望得分 $100\text{pts}$。

$\text{Code:}$

#include<bits/stdc++.h>
//#pragma GCC optimize(2)
const int N=2e3+7;
const int M=2e3+7;
const int R=7;
const long long LONGLONG_INF=0x3f3f3f3f3f3f3f3f;
constexpr int _7[R+1]={1,7,49,343,2401,16807,117649,823543};
constexpr int _5[R+1]={1,5,25,125,625,3125,15625,78125};
constexpr int _first[7]={0,1,2,1,4,3,1};
constexpr int _second[7]={0,1,1,2,4,1,3};
constexpr int _result[7]={0,1,2,2,2,3,3};
constexpr int __first[6][2]={{0,0},{0,1},{1,0},{1,1},{1,0},{1,1}};
constexpr int __second[6][2]={{2,0},{2,1},{1,0},{1,1},{0,0},{0,1}};
constexpr int __result[6][2]={{0,0},{0,1},{0,0},{0,1},{1,0},{1,1}};
int n,m,r,a[N],b[N];
int _h[N],cnt;
int mp[_7[R-1]*6/*<<1*/][2];int mpdown[_7[R-1]*6/*<<1*/];
int upu[1<<R<<R/*<<1*/];int downu[_5[R-1]*6/*<<1*/];
int upv[1<<R<<R/*<<1*/];int downv[_5[R-1]*6/*<<1*/];
int from[_5[R-1]*6*6/*<<1*/][3];int common[_5[R-1]*6*6/*<<1*/];bool vis[_5[R-1]*6*6/*<<1*/];
int tot,tot2;
long long minu[_5[R-1]*4/*<<1*/],minv[_5[R-1]*6/*<<1*/];
struct edge{
    int nxt,v;
}_e[M<<1];
inline void add_edge(int u,int v){
    _e[++cnt].nxt=_h[u],_e[cnt].v=v;
    _h[u]=cnt;
}
inline long long min(const long long &a,const long long &b){
	return a<b?a:b;
} 
long long f[N][1<<R<<R/*<<1*/],ans=LONGLONG_INF;
inline void init(){
	for(int i=0;i<3;i++){
		for(int j=0;j<2;j++){
			for(int k=0;k<_7[r-1];k++){
				int st=i*_7[r-1]*2+j*_7[r-1]+k;//tmp=10,i=0,j=1,k=3;
				for(int p=0;p<r-1;p++){
					mp[st][0]+=_first[k/_7[p]%7]*_5[p];//+1
					mp[st][1]+=_second[k/_7[p]%7]*_5[p];//+2
				}
				mp[st][0]+=(__first[i*2+j][0]*_5[r-1]*2+__first[i*2+j][1]*_5[r-1]);
				mp[st][1]+=(__second[i*2+j][0]*_5[r-1]*2+__second[i*2+j][1]*_5[r-1]);
			}
		}
	}
	memset(downu,-1,sizeof downu);
	memset(downv,-1,sizeof downv);
	for(int i=0;i<(1<<r<<r);i++){
		for(int j=0;j<r-1;j++){
			int tmp1=(i>>j>>r)&1,tmp2=(i>>j>>1)&1;
			if(tmp1==0&&tmp2==1) upu[i]+=_5[j];
			if(tmp1==1&&tmp2==0) upu[i]+=2*_5[j];
			if(tmp1==1&&tmp2==1) upu[i]+=3*_5[j];
			tmp1=(i>>j>>r>>1)&1,tmp2=(i>>j)&1;
			if(tmp1==0&&tmp2==1) upv[i]+=_5[j];
			if(tmp1==1&&tmp2==0) upv[i]+=2*_5[j];
			if(tmp1==1&&tmp2==1) upv[i]+=3*_5[j];
		}
		upu[i]+=((i<<1>>r>>r)&1)*_5[r-1]+(i&1)*_5[r-1]*2;
		upv[i]+=((i>>r)&1)*_5[r-1]*2+((i<<1>>r)&1)*_5[r-1];
		downu[upu[i]]=i;
		downv[upv[i]]=i;
	}
	for(int i=0;i<3;i++){
		for(int j=0;j<2;j++){
			for(int k=0;k<_5[r-1];k++){
				bool flag=0;bool flag2=0;
				int st=i*_5[r-1]*2+j*_5[r-1]+k;
				if(i==2) from[++tot][0]=st,from[tot][1]=st-_5[r-1]*4,from[tot][2]=st-_5[r-1]*2;
				if(j==1) flag2=1;
				for(int p=0;p<r-1;p++){
					//if(from[tot][0]==st&&(k/_5[p]%5==1||k/_5[p]%5==4)) ;
					if(k/_5[p]%5==1) from[++tot][0]=st,from[tot][1]=st-_5[p],from[tot][2]=st,flag=1;
					if(k/_5[p]%5==4) from[++tot][0]=st,from[tot][1]=st-_5[p]-_5[p],from[tot][2]=st-_5[p];
				}
				if(from[tot][0]!=st||flag||(i!=2&&st==0)) common[++tot2]=st;
				if(flag2) vis[st]=1;
			}
		}
	}
	for(int i=0;i<3;i++){
		for(int j=0;j<2;j++){
			for(int k=0;k<_7[r-1];k++){
				int st=i*_7[r-1]*2+j*_7[r-1]+k;
				for(int p=0;p<r-1;p++)
					mpdown[st]+=_result[k/_7[p]%7]*_5[p];
				mpdown[st]+=__result[i*2+j][0]*_5[r-1]*2+__result[i*2+j][1]*_5[r-1];
				mpdown[st]=downu[mpdown[st]];
			}
		}
	}
}
inline void first(int u){
    f[u][1]=0;
    f[u][1<<r]=a[u];
    f[u][1<<r>>1<<r]=min(f[u][1<<r>>1<<r],(long long)b[u]);
}
inline void work(int u,int v){
	memset(minu,0x3f,sizeof minu);
	memset(minv,0x3f,sizeof minv);
	for(int i=1;i<=tot2;i++){
		if(~downu[common[i]]) minu[common[i]]=min(minu[common[i]],f[u][downu[common[i]]]);
		if(~downv[common[i]]) minv[common[i]]=min(minv[common[i]],f[v][downv[common[i]]]);
	}
	for(int i=1;i<=tot;i++){
		if(from[i][0]<_5[r-1]*4)			
			minu[from[i][0]]=min(minu[from[i][1]],minu[from[i][2]]);
		minv[from[i][0]]=min(minv[from[i][1]],minv[from[i][2]]);
		if(vis[from[i][0]]) minv[from[i][0]]=min(minv[from[i][0]],minv[from[i][0]-_5[r-1]]);
	}
}
inline void solve(int u,int v){
	memset(f[u],0x3f,sizeof f[u]);
	for(int i=0;i<3;i++){
		for(int j=0;j<2;j++){
			for(int k=0;k<_7[r-1];k++){
				int tmp=i*_7[r-1]*2+j*_7[r-1]+k;
				int st=mpdown[tmp];
				f[u][st]=min(f[u][st],minu[mp[tmp][0]]+minv[mp[tmp][1]]);
				//if(f[u][st]!=LONGLONG_INF)
				//	printf("u:%d tmp:%d upu[st]:%d st:%d f[u][st]:%d mp[tmp][0]:%d mp[tmp][1]:%d minu[mp[tmp][0]]:%d O:%d minv[mp[tmp][1]]:%d O:%d\n",u,tmp,upu[st],st,f[u][st],mp[tmp][0],mp[tmp][1],minu[mp[tmp][0]],downu[mp[tmp][0]],minv[mp[tmp][1]],downv[mp[tmp][1]]);
			}
		}
	} 
}
inline void dfs(int u,int fa){
    first(u);
    for(int ___=_h[u];___;___=_e[___].nxt){
        int v=_e[___].v;if(v==fa) continue;
        dfs(v,u);work(u,v);solve(u,v);
    }
}
inline void answer(){
    for(int i=0;i<(1<<r);i++) if(ans>f[1][i<<r]) ans=f[1][i<<r];
    printf("%lld\n",ans);
}
int main(){
	memset(f,0x3f,sizeof f);
    scanf("%d%d",&n,&r);
    for(int i=1;i<n;i++){
        int u,v;scanf("%d%d",&u,&v);
        add_edge(u,v);add_edge(v,u);
    }
    for(int i=1;i<=n;i++) scanf("%d%d",&a[i],&b[i]);
    init();dfs(1,0);answer();
    return 0;
}