自动搬运

查看原文

来自洛谷，原作者为

	yummy 这个人是时代的眼泪，什么也没有留下

搬运于2025-08-24 22:43:46，当前版本为作者最后更新于2022-12-31 20:28:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

D 验题人 sol

这里提供一种代码更短的 $O(n)$ 做法。

Update：被当做官方解法拿去讲了，实际上本质相同。

Update：修正一个 typo，添加 Python 程序。

背景

实际上这场比赛的备赛周期非常长。这道题在 8 月就出出来了，当时我就睡觉的时候把这题口胡了，第二天和 JV 讲了，他表示这做法好想好写，觉得这题要被橄榄。但是后来咕咕咕了。再接着到了 12 月。

然后我就退役了。但是一想到这题可能是我在役期间唯一独立完成的 div2D（而且和出题人做法完全不同），我逼自己完成了这个实现，不能让这个奇妙想法就此埋没。

JV 很喜欢三角剖分啊。上次那个 You are the Miserable 也是三角剖分的性质。

做法

当 $n$ 为奇数时显然不存在答案。思考偶数怎么做。

当 $n=2$ 时答案是唯一确定的，接下来思考如果每次增加两个点，我们应该怎么加边，才能维护生成树的性质。

如果我们在原来基础上连续添加一对相邻三角形（左图，增加 $0,2$ 两点），那么可以添加 $(0,4),(2,4)$ 两条边；如果在相邻两条边上各加入一个三角形（右图，增加 $1,2$ 两点），那么可以添加 $(0,1),(0,2)$ 两条边。

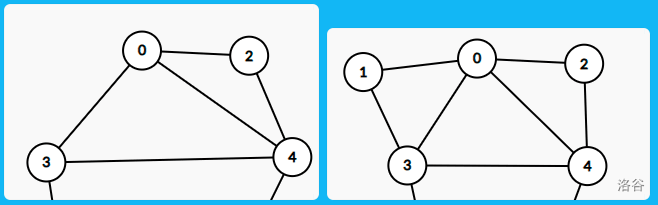
接下来需要证明所有 $n$ 为偶数的三角剖分都可以用这两种方法得到。

如果我们以每个三角形为结点，相邻三角形间连边，那么每个点度数不超过 $3$，是一棵二叉树。

如果我们要给树 $T$ 构造答案，那么：

• 如果 $T$ 的两个孩子都有偶数个三角形，则分别让两个孩子自给自足即可，根等待父亲连边。
• 如果 $T$ 两个孩子都有奇数个三角形，则我们用上面右图的方法连接两个孩子。
• 如果 $T$ 两个孩子一奇一偶，则根应该和奇数子树的根使用左图方法连接。

这样整棵树 $T$ 都能被构造一个合法的答案。

实现

对偶图，听上去好办，实操起来细节很多。

第一个问题是如何给 $n$ 个长度和 $O(n)$，值域为 $n$ 的数列排序。

我们可以采用计数排序，但是如果 $n$ 个数列一起排序只要扫描一次计数器，时间复杂度 $O(n)$。

但是本题因为排序是为了求环上的前驱后继，所以对序列 $u$，大于 $u$ 的放前面，小于 $u$ 的放后面。

同时为了方便查找我们可以放 $n$ 个哈希表，记录每个点在 vector 中的下标。

第二个问题是如何区分三角形的三条边。

这个建议大家边在草稿纸上画图边写，位置关系要和草稿纸严格对应。

我草稿纸上的图 $1\sim n$ 是逆时针排列的，因此我规定 dfs(u,v,w) 中，$u,v,w$ 也是逆时针排列，并且 $(u,v)$ 是当前三角形和父亲之间的界限。这种记法给我带来了很多方便。

写的时候还是脑抽很多次了的。比如说，两次 DFS（一次求子树大小，一次染色）不会带来任何 coding 的方便，徒增常数，直到我 AC 了这道题我才意识到。参考代码如下：

#include<bits/stdc++.h>
using namespace std;
int n;
vector<int> g[300005],ng[300005];
unordered_map<int,int> loc[300005];
#define lc g[u][loc[w][u]+1]
#define rc g[v][loc[w][v]-1]
int tree(int u,int v,int w)//返回值为子树大小
{
	int lsz=0,rsz=0;
	if(not(w==u-1 or w==n and u==1))lsz=tree(u,w,lc);
	if(not(w==v+1 or w==1 and v==n))rsz=tree(w,v,rc);
	if((lsz+rsz)%2)//如果子树大小为偶数
		if(lsz%2==1)
			printf("%d %d\n%d %d\n",u,w,u,lc);
		else
			printf("%d %d\n%d %d\n",v,w,v,rc);
	else if(lsz%2==1)//如果两个奇数那么将两个孩子连起来
		printf("%d %d\n%d %d\n",w,lc,w,rc);
	return lsz+rsz+1;
}
int main()
{
	scanf("%d",&n);
	if(n%2){puts("-1");return 0;} 
	int u,v;
	for(int i=1;i<=n-3;i++)
	{
		scanf("%d%d",&u,&v);
		ng[u].push_back(v);
		ng[v].push_back(u);
	}
	for(int i=1;i<=n;i++)
	{
		ng[i].push_back(i%n+1);
		ng[i%n+1].push_back(i);
	}
	for(int i=1;i<=n;i++)//问题 1：计数排序，i 枚举值
		for(int j:ng[i])
		{
			if(j>i)continue;//j<i 的边在前
			loc[i][j]=g[j].size();
			g[j].push_back(i);
		}
	for(int i=1;i<=n;i++)
		for(int j:ng[i])
		{
			if(j<i)continue;//j>i 的边在后
			loc[i][j]=g[j].size();
			g[j].push_back(i);
		}
	printf("1 2\n");//一开始将 1,2 加入答案
	tree(1,2,g[1][1]);//可以保证这个三角形一定是贴边的，构成二叉树
	return 0;
}

Python 3 解法（虽然常数比较大，无法通过 Subtasks 3 and 6）：

n=int(input())
import sys
sys.setrecursionlimit(300005)
if n%2:
	print(-1)
	sys.exit(0)
ng,g=[[] for i in range(n+5)],[[] for i in range(n+5)]
loc=[{} for i in range(n+5)]
def tree(u,v,w):
	lsz,rsz=0,0
	if not(w==u-1 or w==n and u==1):
		lc=g[u][loc[w][u]+1]
		lsz=tree(u,w,lc)
	if not(w==v+1 or w==1 and v==n):
		rc=g[v][loc[w][v]-1]
		rsz=tree(w,v,rc)
	if (lsz+rsz)%2:
		if lsz%2:
			print("%d %d\n%d %d"%(u,w,u,lc))
		else:
			print("%d %d\n%d %d"%(v,w,v,rc))
	elif lsz%2==1:
		print("%d %d\n%d %d"%(w,lc,w,rc))
	return lsz+rsz+1
for i in range(n-3):
	u,v=map(int,input().split())
	ng[u].append(v)
	ng[v].append(u)
for i in range(1,n+1):
	ng[i].append(i%n+1)
	ng[i%n+1].append(i)
for i in range(1,n+1):
	for j in ng[i]:
		if j<i:
			loc[i][j]=len(g[j])
			g[j].append(i)
for i in range(1,n+1):
	for j in ng[i]:
		if j>i:
			loc[i][j]=len(g[j])
			g[j].append(i)
print(1,2)
tree(1,2,g[1][1])