自动搬运

查看原文

来自洛谷，原作者为

	ande 这个家伙不懒，但还是没有什么东西留下

搬运于2025-08-24 22:43:41，当前版本为作者最后更新于2022-12-26 14:30:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一.简述题意

1.简化题意

给定一个图，无向边，小 A 从 S 点出发，以 2 的速度运动在目标为 F 点的最小字典序最短路上运动，现有一怪物从点 Ｂ 出发，以 3 的速度随机游荡，但怪物无法经过重复的点。小 A 想要在不被抓到的情况下到达 F 点，请问在最坏情况下，小 A 能否逃脱，若能逃脱给出怪兽距离小 A 最近的距离，若不能则最早什么时候能抓到小 A。

2.一些需要注意的点

1.怪兽可以在 F 点抓住小 A。

2.怪兽可以在边上抓到小 A。

（赛时卡了半天瞄了一眼赛时答疑才看到/kk）

3.正搜和倒搜的区别，文中做了详细解释。

二.分析

1.Dijk最短路（记录路径）

题中提到小 A 会按照从 S 到 F 的最短路运动，那么显而易见怪兽只会在这条最短路径上抓住小 A，想要知道能否抓住小 A，只需要对比两者到达同一位置的时间即可，所以我们的第一步就是求出小 A 的路径及怪兽到达路径上每个点的最短时间。注意，此时要求出字典序最小的最短路径，要从 F 点起搜，到达 S 点结束。

此处为什么要倒搜，首先 Dijk 使用根堆优化排序，而堆的第二排序关键字是点的序号，故每次处理出的路径是从终点到出发点的字典序最小最短路径，不是从起点到终点的字典序最小路径，这里解释一下：

根堆处理时，是在有多种合法选择时，会选择最优的，而在选无可选的情况下直接采用，那么就会出现如下情况，即部分最优而非整体最优，下图中从 1 点跑最短路和在 5 点跑最短路路径不同：

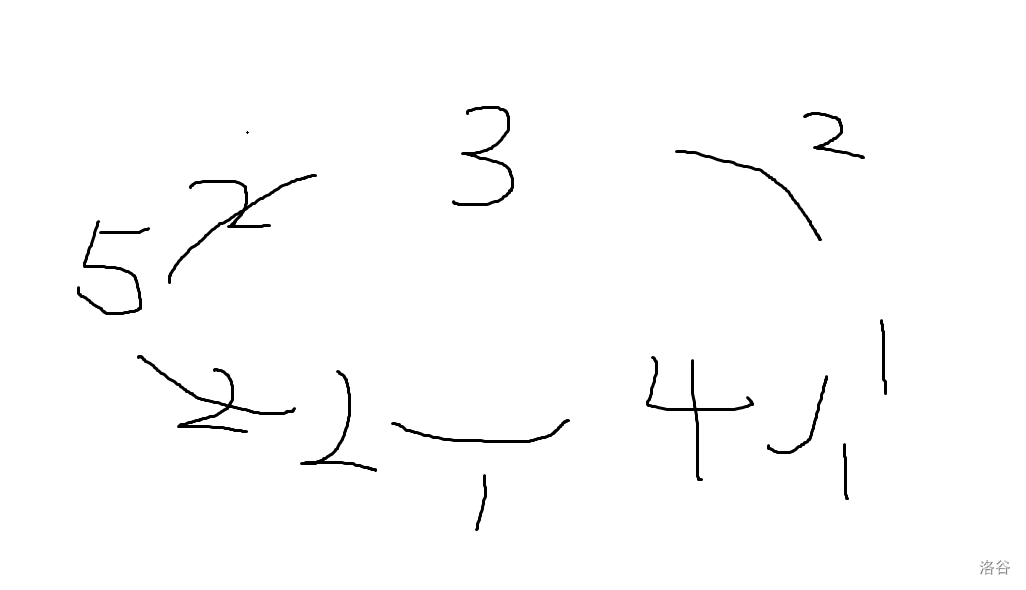
转移时， Dijk 每次找影响相同合法转移点中编号最小的，路径反过来之后相当于找能去的点中编号最小的，显然也是符合字典序最小的，所以这里要采取倒搜的方法。

然后处理出 B 点即怪兽出发点到 F 的单源最短路径，如何记录最短路径？这里联想一下链式前向星的存图方式，使用链表存图，当前点存储连接的下一个点的编号，那么以此类推：

定义一个 $P_i = j$，来表示到达 $i$ 点的最短路径的上一个节点是 $j$ 点 。具体实现在 Dijk 判断中加一行代码即可。具体如下：

 	while ( !pq.empty() ) {
 	    P p = pq.top();
 	    pq.pop();
 	    int now = p.second;
 	    if ( mp[now] == 1 ) continue;
 	    mp[now] = 1;
 	    for ( int i = head[now]; i; i = edge[i].next ) {
 	       int to_ = edge[i].to, val = edge[i].val;
 	       if ( dis1[now] + val == dis1[to_] )
 	          pa[to_] = min( pa[to_], now );//字典序最小
 	       else if ( dis1[to_] > dis1[now] + val ) {
 	          dis1[to_] = dis1[now] + val;
 	          pa[to_] = now;//优先最短路径
 	          pq.push( { dis1[to_], to_ } );
      }
    }
  }
      }

调用的时候注意是需要顺序，所以我们采用队列的方式进行调用，如下：

 	int sign = s;
  	int x = dis1[s];
 	while ( N ) {
    	    dis1[sign] = x - dis1[sign];//倒搜要处理一下距离
    	    q.push( sign );
    	    sign = pa[sign];
     	    if ( sign == 0 ) break;
  }

此时怪兽到达路径的部分我们已经求完了，接下来在挨个遍历的过程中，对于每个点就要判断是下列三种相遇方式中的哪一种，然后按照情况来讨论：

1.两者在同一时间到达同一点：

这种显而易见不再过多赘述。

2.怪兽到达后，需要追上小 A，即追击问题：

这种也很好想，用两者相距距离除以相对速度 1 即可。

3.怪兽到达后，需要与小 A 双向奔赴，即相遇问题：

两者相距距离除以相对速度 5，本质上和第二种情况相同。

然后对每个答案取 $\min$ 值，判断是否能被抓到将 $\min$ 值设为最劣情况即小 A 在安全屋被抓到的时间，最后进行特判即可。

三.坑点

到这里本文应该结束了的，可是毒瘤出题人卡了一下精度，要求有几位输出几位，不得有多余的 $0$ 或 $.$。 我的解决方式是使用双精度浮点型，并使用用 $\operatorname{cout}$ 函数输出，虽然慢但是具有很好的完美符合出题人要求的性质，即输出精确位数。然后被卡到 70 ptsTAT。

测了一下大样例发现问题在于 $\operatorname{cout}$ 默认保留 6 位有效数字，多余的位数用科学记数法表示，所以用一下黑科技:

	cout.precision(15);

修改到 $15$ 位就好啦，溜！

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define P pair< int, int >
const int N = 3e5 + 7;
int n, m, s, B, F;
inline int read() {
  int x = 0, f = 1;
  char ch = getchar();
  while ( ch < '0' || ch > '9' ) {
    if ( ch == '-' ) f = -1;
    ch = getchar();
  }
  while ( ch >= '0' && ch <= '9' ) {
    x = ( x << 1 ) + ( x << 3 ) + ( ch - 48 );
    ch = getchar();
  }
  return x * f;
}
double min( double x, double y ) {
  if ( x < y ) return x;
  return y;
}
struct aa {
  int to, next, val;
} edge[N * 2];
int head[N * 2], t = 1;
void add( int now, int to, int val ) {
  edge[t].to = to;
  edge[t].val = val;
  edge[t].next = head[now];
  head[now] = t++;
}
int dis1[N], dis2[N];
int pa[N];
priority_queue< P, vector< P >, greater< P > > pq;
int mp[N];
void dijk( int s1, int s2 ) {
  memset( dis1, 0x3f, sizeof( dis1 ) );
  memset( dis2, 0x3f, sizeof( dis2 ) );
  dis1[s1] = 0;
  pa[s1] = 0;
  pq.push( { dis1[s1], s1 } );
  while ( !pq.empty() ) {
    P p = pq.top();
    pq.pop();
    int now = p.second;
    if ( mp[now] == 1 ) continue;
    mp[now] = 1;
    for ( int i = head[now]; i; i = edge[i].next ) {
      int to_ = edge[i].to, val = edge[i].val;
      if ( dis1[now] + val == dis1[to_] )
        pa[to_] = min( pa[to_], now );
      else if ( dis1[to_] > dis1[now] + val ) {
        dis1[to_] = dis1[now] + val;
        pa[to_] = now;
        pq.push( { dis1[to_], to_ } );
      }
    }
  }
  while ( !pq.empty() )
    pq.pop();
  pq.push( { 0, s2 } );
  for ( int i = 1; i <= n; i++ )
    mp[i] = 0;
  dis2[s2] = 0;
  while ( !pq.empty() ) {
    P p = pq.top();
    pq.pop();
    int now = p.second;
    if ( mp[now] == 1 ) continue;
    mp[now] = 1;
    for ( int i = head[now]; i; i = edge[i].next ) {
      int to_ = edge[i].to, val = edge[i].val;
      if ( dis2[to_] > dis2[now] + val ) {
        dis2[to_] = dis2[now] + val;
        pq.push( { dis2[to_], to_ } );
      }
    }
  }
}
queue< int > q;
signed main() {
  cout.precision( 15 );
  // freopen("data.in","r",stdin);
  // freopen("data.out","w",stdout);
  n = read(), m = read(), s = read(), B = read(), F = read();
  for ( int i = 1; i <= m; i++ ) {
    int x = read(), y = read(), z = read();
    add( x, y, z );
    add( y, x, z );
  }

  dijk( F, B );

  int sign = s;
  double time = dis1[s] / 2.0;
  int x = dis1[s];
  while ( N ) {
    dis1[sign] = x - dis1[sign];
    q.push( sign );
    // cout << dis1[sign] << " ";
    sign = pa[sign];
    if ( sign == 0 ) break;
  }
  while ( !q.empty() ) {
    int now = q.front();
    // cout << now << " ";
    q.pop();
    if ( dis1[now] / 2.0 - dis2[now] / 3.0 >= 0 ) {
      double x = dis1[now] - ( dis2[now] * 2.0 / 3.0 );
      x /= 5.0;
      time = min( time, dis2[now] / 3.0 + x );
    }
    else {
      double x = ( dis2[now] / 3.0 * 2.0 - dis1[now] );
      time = min( time, dis2[now] / 3.0 + x );
    }
  }
  if ( time == dis1[F] / 2.0 && dis1[F] / 2.0 != dis2[F] / 3.0 ) {
    double ans = dis2[F] - ( dis1[F] * 3.0 / 2.0 );
    cout << "YES";
    puts( "" );
    cout << ans;
  }
  else {
    printf( "NO\n" );
    cout << time;
  }

  return 0;
}