1 条题解
-
0
自动搬运
来自洛谷,原作者为

•́へ•́╬
Unsuccessful Leaving Something attempt搬运于
2025-08-24 22:43:40,当前版本为作者最后更新于2022-12-24 23:46:39,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
思路
预处理 表示区间里所有值都在 之间的区间有多少个。
回答问题时按下图容斥:大正方形减去黄正方形减去绿正方形再加上黄绿重叠就是红色要求的,白色为 所以不考虑。 回答。
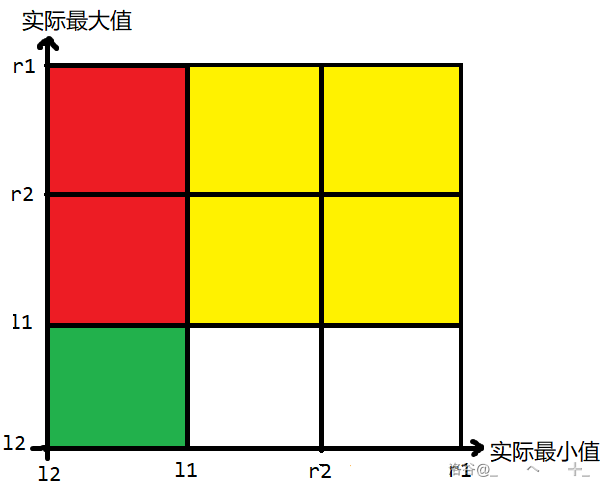
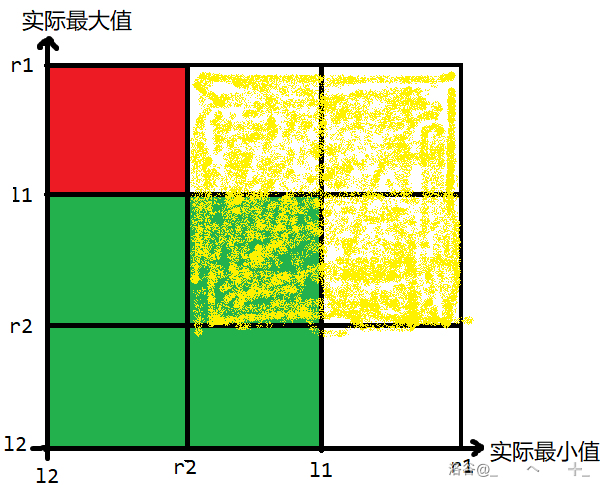
预处理 很简单。 预处理。
code
#include<stdio.h> #include<vector> #define ull unsigned long long #define N 100005 #define M 4002 using namespace std; inline char nc() { static char buf[99999],*l,*r; return l==r&&(r=(l=buf)+fread(buf,1,99999,stdin),l==r)?EOF:*l++; } inline void read(int&x) { char c=nc();for(;c<'0'||'9'<c;c=nc()); for(x=0;'0'<=c&&c<='9';x=(x<<3)+(x<<1)+(c^48),c=nc()); } inline void read(ull&x) { char c=nc();for(;c<'0'||'9'<c;c=nc()); for(x=0;'0'<=c&&c<='9';x=(x<<3)+(x<<1)+(c^48),c=nc()); } int p,q,l[N],r[N];ull xorsum,s,b[M][M]; struct mod { ull b;__int128 m; inline mod(const ull&b):b(b),m(((__int128)(1)<<64)/b){} inline ull reduce(const ull&a) { ull q=m*a>>64; ull r=a-q*b; return r>=b?r-b:r; } }f(2); inline ull rd(){return s^=s<<13,s^=s>>7,s^=s<<17,s;} inline void getlr(int&l1,int&r1,int&l2,int&r2) { l1=f.reduce(rd())+p; r1=f.reduce(rd())+p; l2=f.reduce(rd())+p; r2=f.reduce(rd())+p; if(l1>r1)l1^=r1^=l1^=r1; if(l2>r2)l2^=r2^=l2^=r2; } int n,m,a[N];vector<int>c[M]; main() { read(n);read(m); for(int i=0;i<n;read(a[i]),c[a[i]].emplace_back(i),++i); read(p);read(q);read(s); f=mod(q-p+1); for(int i=p;i<=q;++i) { for(int i=0;i<n;l[i]=r[i]=-1,++i); for(int j=i;j<=q;++j) { b[i][j]=b[i][j-1]; for(int k=0,o;k<c[j].size();++k) { o=c[j][k];l[o]=r[o]=o;++b[i][j]; if(o&&~l[o-1])b[i][j]+=o-l[o-1],r[l[o-1]]=o,l[o]=l[o-1]; if(o<n-1&&~l[o+1]) b[i][j]+=(o-l[o]+1ll)*(r[o+1]-o), l[r[o+1]]=l[o],r[l[o]]=r[o+1]; } } }//预处理 for(int i=1,l1,r1,l2,r2;i<=m;++i) { getlr(l1,r1,l2,r2); if(l2>r1)continue; xorsum^=(b[l2][r1]-b[l2][l1-1]-b[r2+1][r1]+b[r2+1][l1-1])*i; } printf("%llu",xorsum); }
- 1
信息
- ID
- 7505
- 时间
- 500~5000ms
- 内存
- 512MiB
- 难度
- 4
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
