自动搬运

查看原文

来自洛谷，原作者为

	刘辰雨 如果你不想称呼我的全名，你可以以我名称的任意非空后缀来称呼我。

搬运于2025-08-24 22:43:29，当前版本为作者最后更新于2022-12-10 23:01:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

使用算法：拓扑排序

此题非常简单，是拓扑排序模板题，所以我打算讲一讲什么是拓扑排序，以及如何实现拓扑排序。

一、什么是拓扑排序？

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。----百度百科。

看似非常难懂，但是我用人话解释给大家听，意思就是说：

对于一个节点为 $[1,n]$ 的有向图，会有一些 $[1,n]$ 的排列 $^*F$，满足对于图中任意一条 $i \rightarrow j (i,j \in [1,n])$ 的边，$j$ 在排列 $^*F$ 中的位置都在 $i$ 的位置之后。这样的排列叫拓扑排列，求出这个排列的过程叫拓扑排序。

二、如何实现拓扑排序？

实现拓扑排序，说白了，就是求出一种拓扑排列。

为了方便解释，我们定义一条 $i \rightarrow j$ 的边中，$i$ 为 $j$ 的前驱，$j$ 为 $i$ 的后继。每一个节点都可以有多个前驱和多个后继。

那么，不难发现，当我们构造拓扑序列时，考虑一个节点是否应该加入序列时，实际上应该考虑它的全部前驱是否已经在序列里，如果并非如此，那么就不能加入这个节点。

再次考虑一种情况，当我们已经把一个点加入序列后，对它的所有后继而言，它实际上已经失去了影响，换而言之，这个点还在不在已经没有关系了，所以我们可以直接“删去”这个点，将它与它的后继之间的边全部删去。

于是，我们可以得到一份初步的拓扑排序代码：

#include <iostream>
#include <cstdio> 
#include <vector>
#define maxn 5003
using namespace std;

int N /*节点数量*/,M /*边的数量*/ ;
vector<int> Edge[maxn];
/*我个人习惯使用vector存图，vector<int> *Edge[i]表示i的所有后继*/ 
int In[maxn]/*前驱数组，记录每个节点的实时前驱数量*/; 
int G[maxn],tot;/*拓扑序列数组*/

int First,End;
/*临时变量*/

int main()
{
	scanf("%d%d",&N,&M);
	for(int i = 1 ; i<= M ; i++)
	{
		scanf("%d%d",&First,&End);
		Edge[First].push_back(End);
		/*读入并添加一条 First -> End 的边*/
		In[End]++;
		/*记录前驱数量*/ 
	}
	while(tot < N)
	{
		for(int i = 1 ; i<= N ; i++)
		{
			if(In[i] == 0)
			{
				G[++tot] = i;
				for(int Now : Edge[i])
					In[Now]--;
				/*遍历 vector<int> *Egde[i]，改变i的所有后继的前驱数组数量*/
			}
		}
	}
	for(int i = 1 ; i<= N ; i++)
		printf("%d ",G[i]);
	puts(""); 
	return 0;
}

输入数据：

6 8
1 3
1 5
1 6
2 5
2 6
3 4
3 5
5 6

输出（拓扑序列）：

1 2 3 4 5 6

解释：

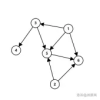
该有向图为如下：

可以尝试对比理解。

代码优化：

当你理解以后，就会发现这份代码慢得kou难以忍受，稍微卡一卡，就可以到 $\mathcal{O(n^2)}$ 的时间复杂度。所以，我们需要优化。

仔细思考，当一个节点从有前驱变成无前驱，只有可能是它的最后一个前驱被加入了序列的那一瞬间！那么我们只要抓住这个“瞬间”，结合 $dijkstra$ 的优化方式，不难想到使用队列优化。

具体请看优化代码：

#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#define maxn 5003
using namespace std;

int N,M;
vector<int> Edge[maxn];
int In[maxn];
int G[maxn],tot;

int First,End;
queue<int> Q;

int main()
{
	scanf("%d%d",&N,&M);
	for(int i = 1 ; i<= M ; i++)
	{
		scanf("%d%d",&First,&End);
		Edge[First].push_back(End);
		In[End]++;
	}
	for(int i = 1 ; i<= N ; i++)
		if(In[i] == 0)
			Q.push(i);
	while(!Q.empty())
	{
		int u = Q.front();
		Q.pop();
		G[++tot] = u;
		for(int Now : Edge[u])
		{
			In[Now]--;
			if(In[Now] == 0)
				 Q.push(Now);
		}
	}
	for(int i = 1 ; i<= tot ; i++)/*tot = n*/
		printf("%d ",G[i]);
	puts("");
	return 0;
}

通过这种方式，可以省掉不必要的遍历，对于稀疏图，可以大大减少时间复杂度，降低了被卡的可能性。（不过很遗憾，对于完全图，它会退化成朴素算法

三、此题该怎么做？

非常简单，求拓扑序列的同时记录每道题完成的天数，当序列求到编号为 $K$ 的题时，输出完成天数并结束程序即可。若程序一直执行到最后，输出-1。

具体看代码：

#include <iostream>
#include <cstdio>
#include <vector>
#include <bitset> 
#include <queue>
#define maxn 5003
using namespace std;

vector<int> Edge[maxn];
bitset<maxn> Avai;
int N,K,p;
int R;
int In[maxn];

int First,End,Num;

queue<pair<int,int> > Q;

int main()
{
	while(!Q.empty())
		Q.pop();
	scanf("%d%d%d",&N,&K,&p);
	for(int i = 1 ; i<= p ; i++)
	{
		scanf("%d",&Num);
		Avai[Num] = true;
		Q.push({Num,0});
	}
	scanf("%d",&R);
	for(int i = 1 ; i<= R ; i++)
	{
		scanf("%d%d",&End,&Num);
		while(Num--)
		{
			scanf("%d",&First);
			Edge[First].push_back(End);
			In[End]++;
		}
	}
	while(!Q.empty())
	{
		pair<int,int> u = Q.front();
		Q.pop();
		int ID = u.first;
		int Day = u.second;
		if(!Avai[ID])
			continue;
		if(ID == K)
		{
			printf("%d\n",Day);
			return 0;
		}
		for(int End: Edge[ID] )
		{
			In[End]--;
			if(In[End] == 0)
			{
				Avai[End] = true;
				Q.push({End,Day+1});
			}
		}
	}
	puts("-1");
	return 0;
}

写在最后：

首先，此题较为简单，

建议评 $\textcolor{#FFC116}{Popularization/Enhancement-}$。

其次，

好久没写过这么水的T3啦，感谢UOI让我重振信心！！ 比赛很赞！