自动搬运

查看原文

来自洛谷，原作者为

	Vct14 **

搬运于2025-08-24 22:43:26，当前版本为作者最后更新于2022-12-06 13:48:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目传送门 || 更好的阅读体验 || 更新日志

思路

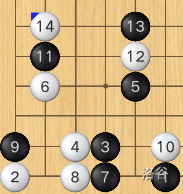
以下用黑棋代表小 A 下的“柯基”，用白棋代表小 B 下的“柯基”。黑棋先手。

通过探索，我们可以发现以下规律：

• 当棋盘边长为奇数时，黑棋先下棋盘中心（一个交叉点），然后以棋盘的中心对称，那么白棋能下的地方，黑棋也能下，那么最后一步一定是黑棋下的，即黑棋获胜；

• 当棋盘边长为偶数时，以棋盘的中心线对称，无论黑棋下哪里，白棋就下它的对称点，那么黑棋能下的地方，白棋也能下，那么最后一步一定是白棋下的，即白棋获胜。这里中心线指将棋盘对折一次形成的折痕（这么说有点奇怪，不过理解意思就行（逃））。

由 $x_i$ 的生成器中的 x[i]=x[i-1]+((xor_shift(seed)%(unsigned long long)(2*2)+1))*2; 可知 $x_i$ 为偶数，即小 C 捣乱时先后手的顺序不变。

由于捣乱时，棋盘的中心和中心线、棋盘边长的奇偶性、先后手顺序都不变，所以捣乱前和捣乱后赢家是不变的。

综上所述，

• 当棋盘的边长为奇数时，小 A 胜；
• 当棋盘的边长为偶数时，小 B 胜。

代码

#include<bits/stdc++.h>
using namespace std;

int main(){
	int T;
	cin>>T;
	while(T--){
		int n,q,seed;
		cin>>n>>q>>seed;
		if(n%2) cout<<"A won";
		else cout<<"B won";
		cout<<"\n";
	}	
	return 0;
}

提示：

• 本题为多组测试数据。
• 虽然本题的 $q$ 和 $seed$ 没有用上，但是不要漏输入。