自动搬运

查看原文

来自洛谷，原作者为

	离散小波变换° 有志不在年高，无志空长百岁

搬运于2025-08-24 22:43:20，当前版本为作者最后更新于2022-11-27 08:57:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题解

压轴题。

容易发现这是一棵树。具体可以用归纳法。设前 $i$ 行组成一棵树，那么第 $i+1$ 行内每个点都向第 $i$ 行某个点连了边，那肯定前 $i+1$ 行也是一棵树了。

容易发现这树很特殊。它的点数达到了 $n^2$ 级别，但是第 $i$ 列整个就是串在一起的形成链的样子。可以证明，整棵树可以被划分为 $\mathcal O(n)$ 个点和 $\mathcal O(n)$ 条链。

定义：我们选出树上一些点作为关键点。这些点包括第 $1$ 层的所有点、第 $n$ 层的所有点、其他所有度数为 $3$ 的点。

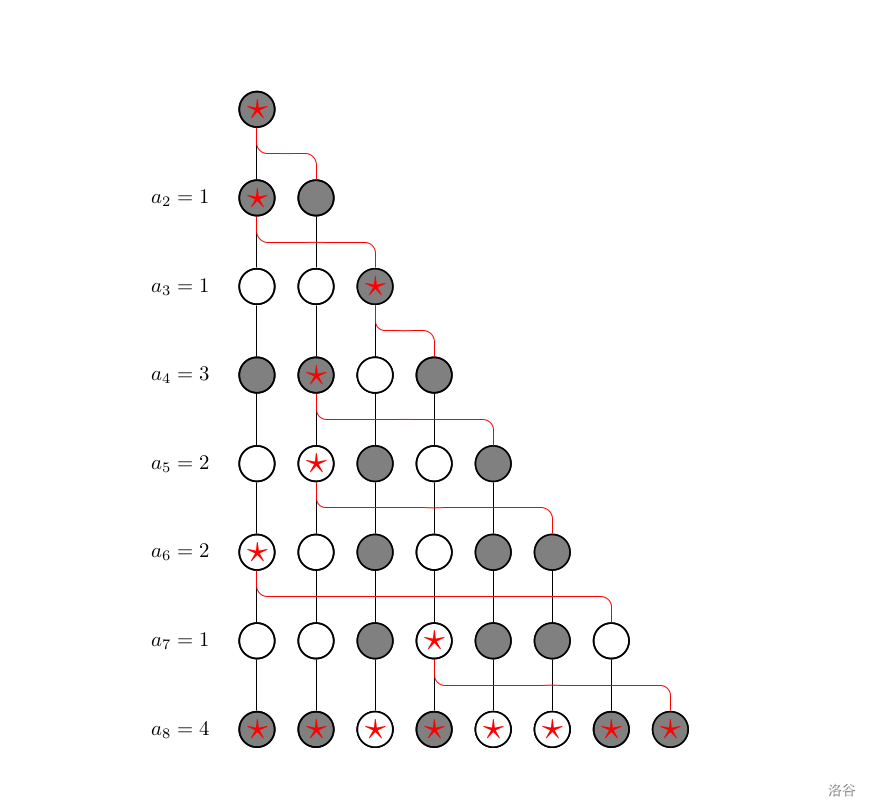
图中标上红星的即为关键点。

断言：关键点的个数是 $\mathcal O(n)$ 级别的。

证明：考虑前 $i$ 行，$i\ge 2$。容易发现，第 $i$ 行所有点的度数应该恰好为 $1$。当加入第 $i+1$ 行的所有点以及边时，第 $i+1$ 行前 $i$ 个点连的边使得第 $i$ 行所有点度数都变成了 $2$，而第 $i+1$ 行第 $i+1$ 个点连的边使得第 $i+1$ 行恰好有一个点度数变成了 $3$，这个点就成了关键点。那么，第 $2\sim (n-1)$ 行应该均恰好有一个特殊点。再加上第 $1$ 行与第 $n$ 行的点，特殊点的总个数就是 $\mathcal O(n)$ 级别的了。

除了关键点，其他所有点的度数均为 $2$（读者自证不难）。于是别的点肯定会在某条链上。沿着链走，走到的两端肯定都是关键点。于是，我们可以把一条链抽象成连接两个关键点的「边」，这个「虚树」节点个数为 $\mathcal O(n)$，那么它的边的个数肯定也是 $\mathcal O(n)$。

把虚树建好后，可以用非常经典的树上最大点权独立集的动态规划做法在虚树上跑。我们关心的是两个关键点之间应该怎么转移。换言之，我们需要知道连接两个关键点的链它的贡献怎么计算。

记 $f_u,g_u$ 分别表示，在选择/不选择虚树上的节点 $u$ 的情况下，子树 $u$ 能取得的最大点权独立集的值。

假设有两个关键点 $u,v$，他们之间通过链 $s=\{p_1,p_2,\cdots p_t\}$ 连接。那么 $v$ 对 $f_u$ 的贡献是 $\max\{\operatorname{val}(p_2,p_3,\cdots,p_t)+g_v,\operatorname{val}(p_2,p_3,\cdots,p_{t-1})+f_v\}$，$v$ 对 $g_u$ 的贡献是 $\max\{\operatorname{val}(p_1,p_2,\cdots,p_t)+g_v,\operatorname{val}(p_1,p_2,\cdots,p_{t-1})+f_v\}$。其中 $\operatorname{val}(p_1,p_2,\cdots,p_t)$ 表示序列 $p$ 在不能选择相邻元素的情况下可以取得的最大点权独立集。我们需要知道，$s$ 序列在「首项/末项」「能选/不能选」共 $4$ 种组合的情况下，分别计算出来的最大点权独立集是多少。

注意一个重要性质：

• 对于每一条连接了两个关键点的链，这条链上的点（不包含顶头的两个关键点），肯定在同一列上。

这同样容易证明。由于该树特殊的构造方法，对于 $j<i$，非特殊点 $(i,j)$ 肯定与 $(i+1,j)$ 和 $(i-1,j)$ 相连，那么这三个点肯定在同一列；对于 $(i,i)$，它向上连接的点肯定是关键点，向下连接的点肯定与它在同一列。于是容易发现每条链上的非特殊点必然在同一列。

那么一条链可以被映射到 $01$ 序列 $r$ 上的一段区间 $[a,b]$。假设这个链在第 $k$ 列。如果 $c_k=0$，那么这个区间内每个位置的权值就是 $r_a,r_{a+1},\cdots,r_b$；如果 $c_k=1$，那么这个区间内每个位置的权值就是 $\neg r_a,\neg r_{a+1},\cdots,\neg r_b$。

问题转化为了，查询对 $r$ 序列或者 $\neg r$ 序列（这两个都是 $01$ 序列）做区间最大点权独立集的结果。

对于 $01$ 序列，计算最大点权独立集是可以采用贪心思想的。比如，对于长度为 $2k$ 的全 $1$ 段，它的最大点权独立集显然是 $k$；对于长度为 $2k+1$ 的全 $1$ 段，它的最大点权独立集显然是 $k+1$。对于含有 $0$ 的序列，总是可以以 $0$ 作为分隔符划分出各种全 $1$ 段，分别求和再相加就行。

那么怎么对 $01$ 序列做区间最大点权独立集呢？

我们预处理两个东西：

• $h_i$，表示仅考虑前 $i$ 个元素，算出的最大点权独立集的结果。
• $p_i$，表示第 $i$ 个元素所处的全 $1$ 段最后一个 $1$ 的位置。特别地，若 $i$ 位置是 $0$，那么 $p_i=i$。

容易预处理上面的两个数组。现在要计算 $[l,r]$ 区间的最大点权独立集，那么结果就是：

$$h_r-h_{\min\{r,p_l\}}+\lfloor(\min\{r,p_l\}-l)/2+1\rfloor $$

解释：使用做差的方法计算出 $[\min\{r,p_l\}+1,r]$ 这一段的最大点权独立集的值，再加上 $[l,\min\{r,p_l\}]$ 这个全 $1$ 段的贡献。

最后讲讲怎么建虚树。维护 $F_i$ 表示第 $i$ 列从最下面往上走走到的关键点的编号。当 $(i,i)$ 位置往 $(i-1,a_i)$ 连边时，$(i-1,a_i)$ 变成了第 $a_i$ 列最靠下的关键点，作为虚树的一员它首先要和 $F_{a_i}$ 连上边，然后更新 $F_{a_i}$ 的值。因为最后一行全部都会是关键点，所以最后再将它们变成关键点与 $F_i$ 连边即可。

于是这题就做完了。

参考代码

#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const i64 INF = 1e18;
int n;
int qread(){
    int w=1,c,ret;
    while((c = getchar()) >  '9' || c <  '0') w = (c == '-' ? -1 : 1); ret = c - '0';
    while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0';
    return ret * w;
}
const int MAXN = 1e6 + 3;
const int MAXM = 2e6 + 3;
int R[MAXN], C[MAXN], A[MAXN], F[MAXN], G[MAXM], W[MAXM], o = 0;
int X[MAXM]; i64 U[MAXM][4];
int Y[MAXM]; i64 V[MAXM][4];
int P0[MAXN], Q0[MAXN], P1[MAXN], Q1[MAXN];
int value(int w){return w % 2 == 1 ? w / 2 + 1 : w / 2;}
void calc(int l, int r, i64 &w, bool t){    // [l, r] 区间
    if(r - l + 1 ==  0){w = 0   ; return;}
    if(r - l + 1 == -1){w = 0   ; return;}
    if(r - l + 1 == -2){w = -INF; return;}
    if(t == false){
        int u = min(Q0[l], r); w = P0[r] - P0[u] + ( R[l] == 1 ? value(u - l + 1) : 0);
    } else {
        int u = min(Q1[l], r); w = P1[r] - P1[u] + (!R[l] == 1 ? value(u - l + 1) : 0);
    }
}
void calc(int l, int r, i64 O[4], bool t){  // [l + (0~1), r - (0~1)] 区间
    calc(l    , r    , O[0b11], t);
    calc(l    , r - 1, O[0b10], t);
    calc(l + 1, r    , O[0b01], t);
    calc(l + 1, r - 1, O[0b00], t);
}
i64 I[MAXM], J[MAXM];   // I 是必须选上，J 是必须不选
void dfs(int u){
    if(X[u] == 0) I[u] = W[u], J[u] = 0; else {
        int l = X[u], r = Y[u]; dfs(l), dfs(r);
        I[u] = W[u]
            + max(U[u][0b00] + I[l], U[u][0b01] + J[l])
            + max(V[u][0b00] + I[r], V[u][0b01] + J[r]);
        J[u] =
            + max(U[u][0b10] + I[l], U[u][0b11] + J[l])
            + max(V[u][0b10] + I[r], V[u][0b11] + J[r]);
    }
}
int main(){ 
    n = qread();
    up(1, n, i) R[i] = qread();
    up(1, n, i) C[i] = qread();
    up(2, n, i) A[i] = qread();
    P0[1] = R[1], P1[1] = !R[1];
    up(2, n, i){
        P0[i] = max(P0[i - 1], P0[i - 2] +  R[i]);
        P1[i] = max(P1[i - 1], P1[i - 2] + !R[i]);
    }
    Q0[n] = Q1[n] = n;
    dn(n - 1, 1, i){
        if( R[i] == 0) Q0[i] = i; else
            if( R[i + 1] == 0) Q0[i] = i; else Q0[i] = Q0[i + 1];
        if(!R[i] == 0) Q1[i] = i; else
            if(!R[i + 1] == 0) Q1[i] = i; else Q1[i] = Q1[i + 1];
    }
    up(1, n - 1, i){
        int t = A[i + 1], f = F[t]; // (i, t) 是特殊点
        F[t] = F[i + 1] = ++ o;     // 给特殊点分配编号
        if(f)
            if(X[f]) Y[f] = o, calc(G[f] + 1, i - 1, V[f], C[t]);
            else     X[f] = o, calc(G[f] + 1, i - 1, U[f], C[t]);
        W[o] = R[i] ^ C[t], G[o] = i;
    }
    up(1, n, i){    // 最后一层都是特殊点
        int t = i, f = F[t]; ++ o, W[o] = R[n] ^ C[i];
        if(f)
            if(X[f]) Y[f] = o, calc(G[f] + 1, n - 1, V[f], C[t]);
            else     X[f] = o, calc(G[f] + 1, n - 1, U[f], C[t]);
    }
    dfs(1); printf("%lld\n", max(I[1], J[1]));
    return 0;
}