自动搬运

查看原文

来自洛谷，原作者为

	Chy12321 Supercalifragilisticexpialidocious!

搬运于2025-08-24 22:43:16，当前版本为作者最后更新于2022-12-06 19:18:16，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

只有 B 国炸毁了图的割边，才会使得图不连通，进而可能会导致军营不连通。也就是说，A 国可以随意地看守或不看守不是割边的边。因此想到 边双缩点 后树形 DP。

为什么边双缩点后会形成一棵树呢？

题目保证了给定的图连通，那么缩点后的图也必然连通，而如果有多个“双连通分量”构成了环，就不符合双连通分量的定义了，即这些首尾相连构成环的“双连通分量”应该被划在同一个双连通分量中。

因此，缩点后形成的图连通且无环，也就形成了一棵树。

已经缩了点，再思考：究竟要在缩点后形成的树上求什么？

令 $V_u$ 表示双连通分量 $u$ 中的点数，$E_u$ 表示双连通分量 $u$ 中的边数，若有 $n$ 个双连通分量，则问题转化为：

给定一棵无根树，每个结点有 $2^{E_u}$ 种不建造军营的方案和 $(2^{V_u + E_u} - 2^{E_u})$ 种建造军营的方案。求共有多少种建造军营的方案（不能不建）。

这里假定 $1$ 号结点为树根。

令 $f(u, 0/1)$ 表示以 $u$ 为根的子树中没有/有军营的方案数。

发现每种状态所涵盖的情况过多，根本不好转移。

这时，有两种思路：

• 增加状态数量。
• 对状态增添限制。

我选择的是后者。

令 $f(u, 0/1)$ 表示以 $u$ 为根的子树中没有/有军营的方案数，若有军营，则所有的军营必须通过已经派兵看守的边与 $u$ 连通。

在想转移之前，为了防止做无用功，最好先想想该如何统计答案。

对于每个结点 $u$，我们强制 $u$ 子树外的所有点都不建军营，同时强制不选 $fa_u \to u$ 的边，再累加方案数，即可保证不重不漏（具体可看下图）。

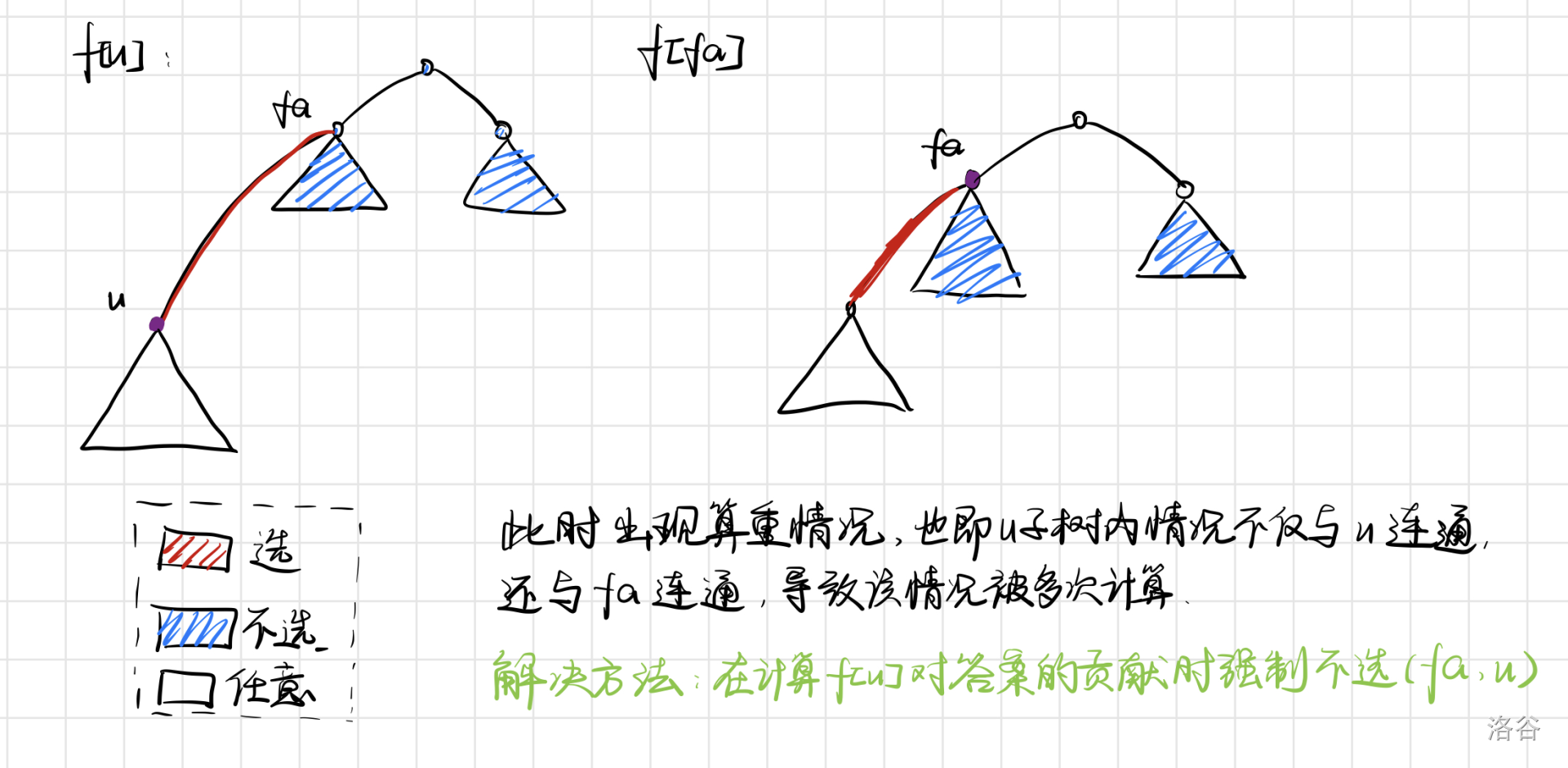
令 $s(u)$ 表示以 $u$ 为根节点的子树内边数，即 $s(u) = E_u + \sum\limits_{v \in son(u)} [s(v) + 1]$，则有 $ans \leftarrow f(u, 1) \times 2^{s(1) - s(u) - 1}$。

特殊地，对于 $1$ 号结点，不存在 $fa_1 \to 1$ 的边，此时 $ans \leftarrow f(1, 1)$。

明确了答案如何统计，接下来考虑转移：

显然地，$f(u, 0) = 2^{E_u} \times \prod\limits_{v \in son(u)} 2f(v, 0)$，难点在 $f(u, 1)$ 的转移上。

考虑每新增一个子节点 $v$ 对 $f(u, 1)$ 产生的贡献。

若到新增前都还未建造一个军营，则以 $v$ 为根的子树中必须有军营，即 $f(u, 1) \leftarrow f(u, 0) \times f(v, 1)$。

若到新增前已经建造过军营，则以 $v$ 为根的子树中有没有军营皆可，且当以 $v$ 为根的子树中没有军营时，$v$ 点是否与 $u$ 点连通皆可，即 $f(u, 1) \leftarrow f(u, 1) \times [2f(v, 0) + f(v, 1)]$。

综上，$f(u, 1) \leftarrow f(u, 0) \times f(v, 1) + f(u, 1) \times [2f(v, 0) + f(v, 1)]$。

初始时，$f(u, 0) = 2^{E_u}$，$f(u, 1) = 2^{V_u + E_u} - 2^{E_u}$。

代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

constexpr int N = 500100, M = 1000100, MOD = 1e9 + 7;

int n, m, p;
int tot, tot2, head[N], head2[N];
int cnt, top, stk[N], dfn[N], low[N], bel[N];
int deg[N], V[N], E[N], s[N];
bool ins[N];
ll ans, f[N][2];

struct Edge {
    int to, nxt;
} e[M << 1], e2[M << 1];

void add(int u, int v) {
    e[++tot] = Edge{v, head[u]};
    head[u] = tot;
}

void add2(int u, int v) {
    e2[++tot2] = Edge{v, head2[u]};
    head2[u] = tot2;
}

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++cnt, ins[stk[++top] = u] = 1;
    for (int i = head[u], v; i; i = e[i].nxt) {
        v = e[i].to;
        if (v == fa) continue;
        if (!dfn[v]) tarjan(v, u), low[u] = min(low[u], low[v]);
        else if (ins[v]) low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u]) {
        p++; int x;
        do {
            // 因为不需要知道每个边双连通分量里都有哪些点，只记录每个点属于哪个边双连通分量即可。
            ins[x = stk[top--]] = 0, bel[x] = p;
            V[p]++; // 累加该边双连通分量内点数
        } while (x != u);
    }
}

ll qp(ll base, int e) { // 快速幂
    ll res = 1;
    while (e) {
        if (e & 1) res = res * base % MOD;
        base = base * base % MOD;
        e >>= 1;
    }
    return res;
}

void dfs(int u, int fa) { // dfs 计算 s[]
    s[u] = E[u];
    for (int i = head2[u], v; i; i = e2[i].nxt) {
        v = e2[i].to;
        if (v == fa) continue;
        dfs(v, u); s[u] += s[v] + 1;
    }
}


void dp(int u, int fa) { // 树形 DP
    for (int i = head2[u], v; i; i = e2[i].nxt) {
        v = e2[i].to;
        if (v == fa) continue;
        dp(v, u);
        // 状态转移
        f[u][1] = (f[u][1] * (((f[v][0] << 1) + f[v][1]) % MOD) % MOD + f[u][0] * f[v][1] % MOD) % MOD;
        f[u][0] = f[u][0] * ((f[v][0] << 1) % MOD) % MOD;
    }
    // 统计答案
    if (u == 1) ans = (ans + f[u][1]) % MOD; // 特判 1 号结点的特殊情况
    else ans = (ans + f[u][1] * qp(2, s[1] - s[u] - 1)) % MOD;
}

int main() {
    ios::sync_with_stdio(0); cin.tie(nullptr), cout.tie(nullptr);
    cin >> n >> m;
    while (m--) {
        int u, v; cin >> u >> v;
        add(u, v), add(v, u);
    }
    tarjan(1, 0); // 边双缩点
    for (int u = 1; u <= n; u++) {
        for (int i = head[u], v; i; i = e[i].nxt) {
            v = e[i].to;
            if (bel[u] != bel[v]) add2(bel[u], bel[v]); // 如果属于两个不同的边双连通分量，则将这两个边双连通分量连边
            else E[bel[u]]++; // 否则该双连通分量内边数 + 1
        }
    }
    for (int i = 1; i <= p; i++) {
        E[i] >>= 1; // 因为是无向边，每一条边会累加 2 次，故 E[i] 需要除以 2
        // 赋初值
        f[i][0] = qp(2, E[i]);
        f[i][1] = qp(2, V[i] + E[i]) - f[i][0];
    }
    dfs(1, 0); dp(1, 0);
    cout << ans;
    return 0;
}

upd on 2022.12.18

感谢 @一只绝帆 指出了一处笔误。

upd on 2023.5.15

针对 @vector 指出的错误修改了部分内容。