[NOIP2022] 喵了个喵

0
15011418730 LV 7 @ 2025-8-24 22:43:15
自动搬运

查看原文

来自洛谷，原作者为

dapingguo8
The Velati∅n

搬运于2025-08-24 22:43:15，当前版本为作者最后更新于2022-11-28 11:33:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

消除的基本策略

假定当前牌堆顶的牌的种类为 $x$ ，现在场上也有至少一张种类为 $x$ 的牌，然后我们想把这张牌直接消掉。

在以下的策略中如果场上有两张相同的牌，我们一定会立刻将它们消掉，所以同种类的牌于此条件下在场上只能出现一次。假定场上另一张种类为 $x$ 的牌位于栈 $p_x$ 中。
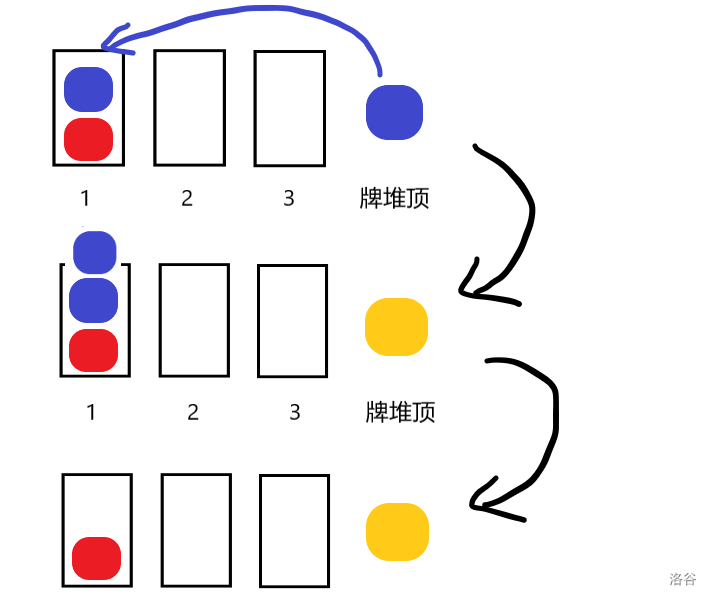
- 如果 $p_x$ 的顶端卡牌种类为 $x$ ，则将当前牌堆顶的牌放到栈 $p_x$ 上，它们会自动被消掉。
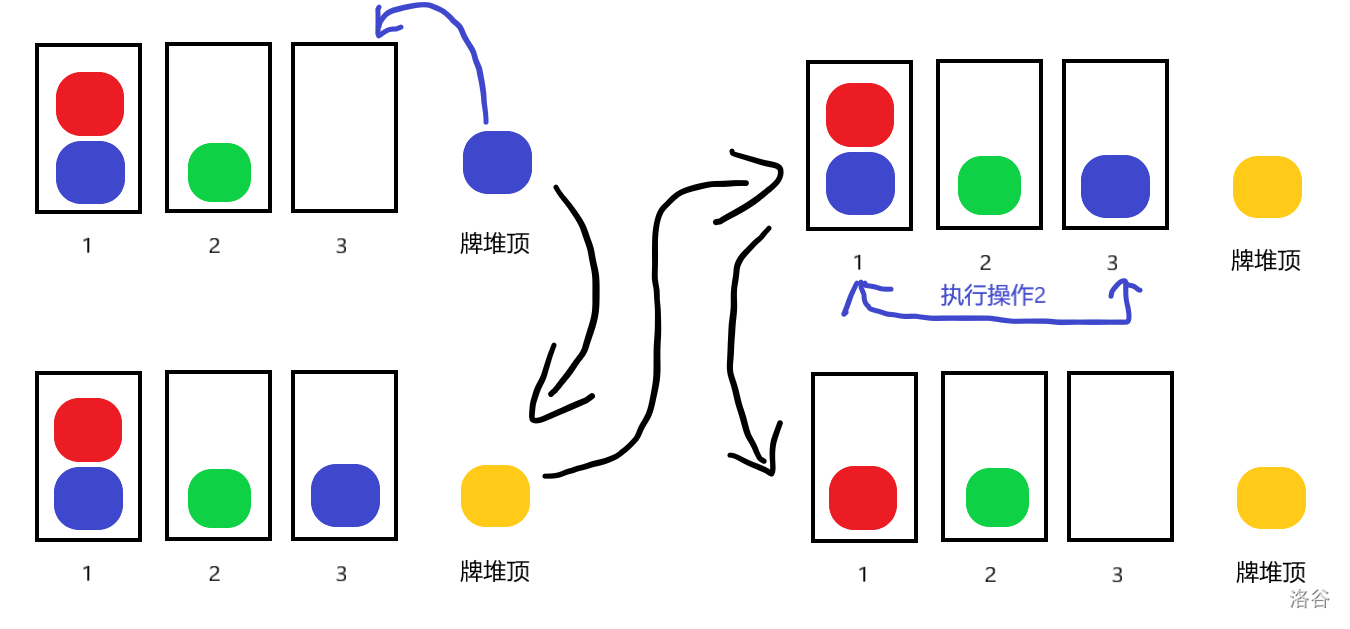
- 如果 $p_x$ 的底端卡牌种类为 $x$ ，则将当前牌堆顶的牌放到一个空栈 $sp$ 上，然后对栈 $sp$ 和 $p_x$ 执行一次操作二，它们也会被消掉。
（以下同颜色代表同种类的牌）

第一种操作示例：

第二种操作示例：

不难发现如果一个栈里有不少于三张牌的话，那么位于中间的那一张是不容易被消掉的，而 $k$ 的范围在 $2n$ 左右，这启发我们尽可能使每个栈含有不超过两张牌。

$k=2n-2$

策略1：存在一个编号为 $sp$ 的空栈，且当前牌堆顶的牌在场上存在或其余栈中存在至少一个栈大小不超过 $1$ ：
- 如果当前牌堆顶的牌在场上出现过，按上述消除基本策略执行（将栈 $sp$ 第二种消除操作的空栈）。
- 否则将其放到任意一个其中大小不超过 $1$ 的栈的栈顶 （ $sp$ 号栈除外）。
由于只有 $k=2n-2$ 种卡牌，我们可以保证即使前 $n-1$ 个栈均含有两张卡牌时，牌堆顶的牌也一定会在场上出现过，可以重复按照策略1执行。令 $n$ 号栈为 $sp$ 空栈，便可保证第二种消除基本策略的执行。

$k=2n-1$

现在多了一种牌，所以策略1不一定每次都能奏效了。

那么考虑如何安置多出来的这一种牌。我们再看牌堆顶的下一张牌，如果这张牌的同类牌出现在栈底（不妨设对应栈编号为 $p$ ），那么不难得出可以将牌堆顶的牌放到栈 $p$ 上，然后将下一张牌放到栈 $sp$ 里，最后对栈 $p$ 和 $sp$ 执行一次操作2便可安置。

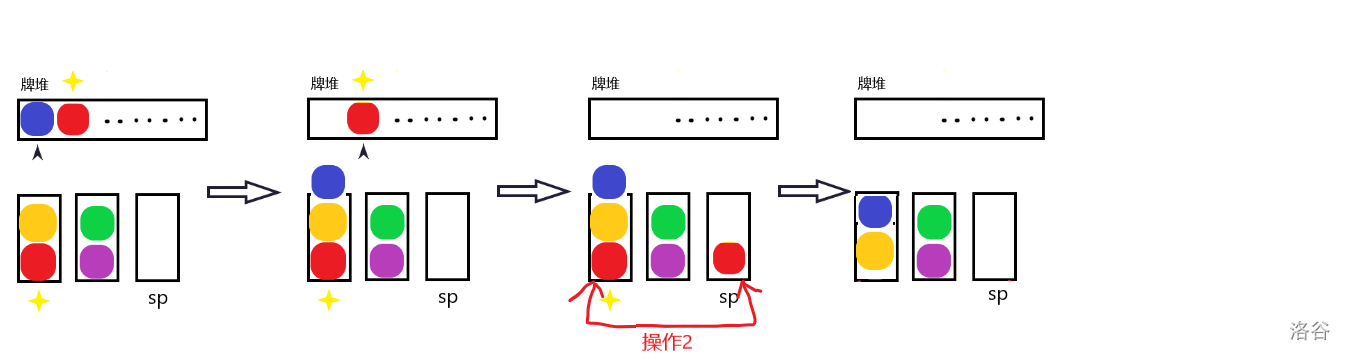
但是如果下一张牌的同类牌在栈顶的话，我们可以无脑将牌堆顶的牌放到栈 $sp$ 上吗？显然不可以：

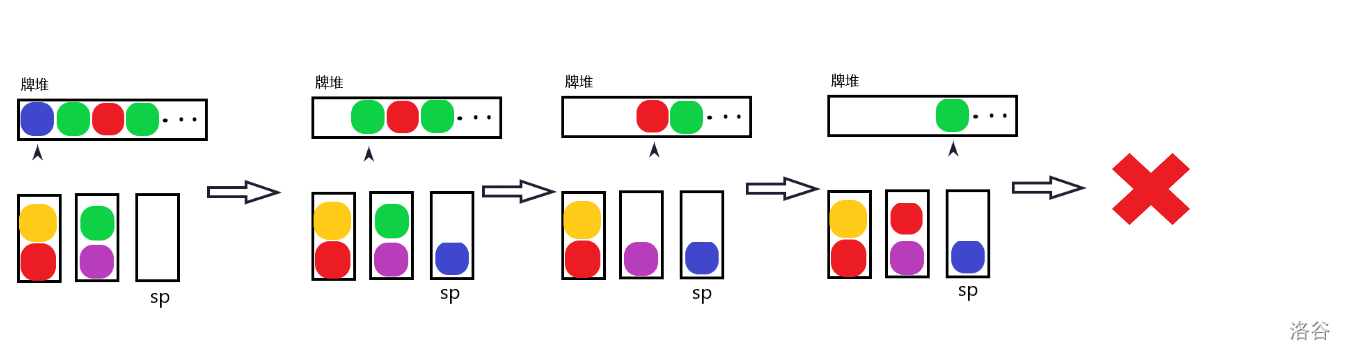
既然消除的关键还是栈底的牌，所以我们可不可以拓宽一下视野，往后看有没有位于底部的牌，然后将牌堆顶的牌放到对应栈顶呢？

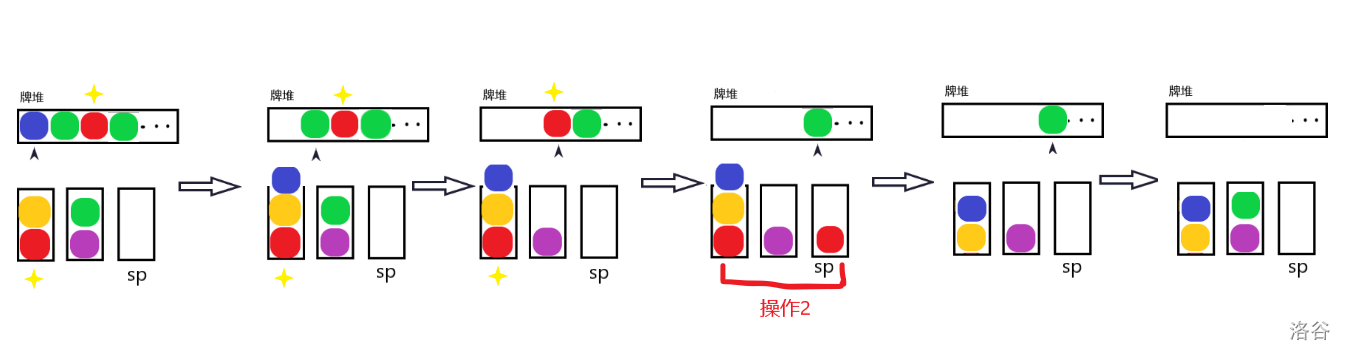
貌似很行，对吧。

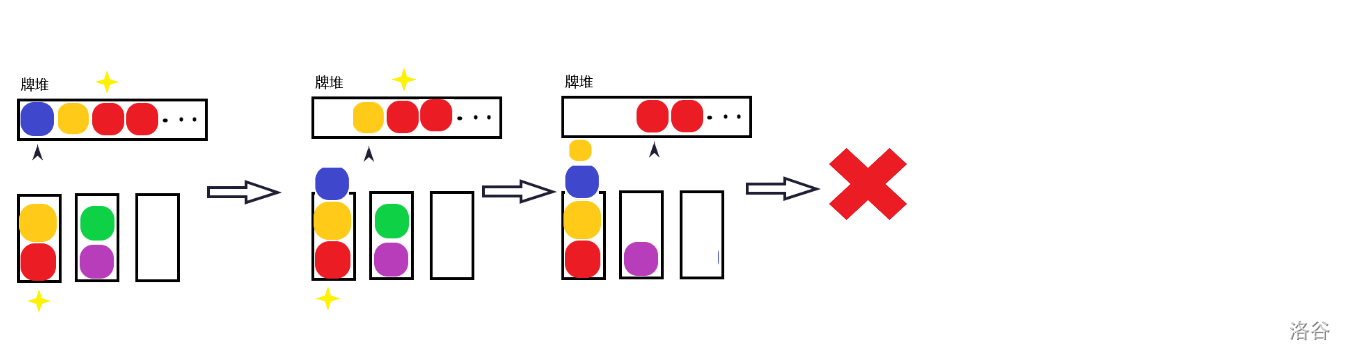
还是不行。牌堆顶的牌阻挡了原栈顶的牌，使得它们不能互相消除。

但如果我们改为将牌堆顶的牌放到 $sp$ 里....

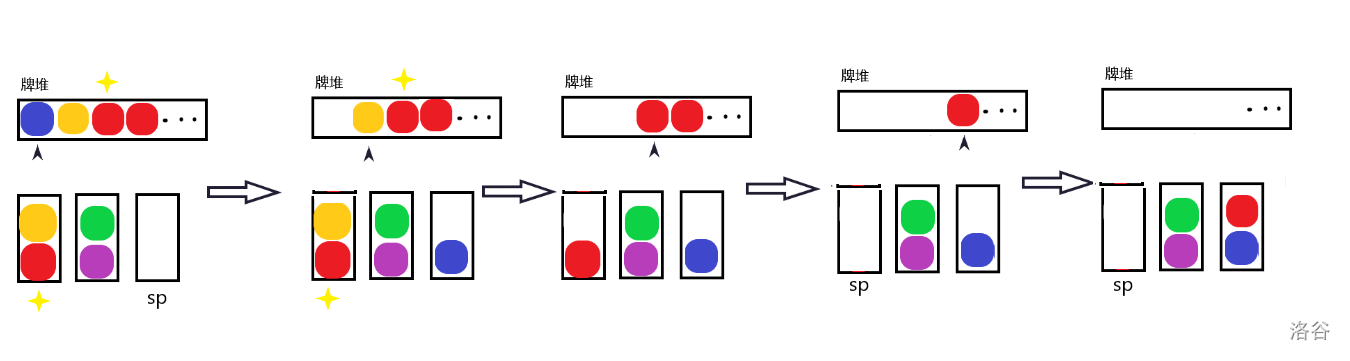
这样反而行得通了，唯一的区别就是 $sp$ 换了一下。

那么两者的区别是什么呢？仔细观察就可以发现：
- 前者第一张位于底部的牌所在栈的栈顶牌没有被消去，后者被消去了。
什么情况下栈顶元素会被消去？结合上述图思考一下便可得知：
- 在牌堆顶和其后第一张位于栈底的牌之间，与栈顶牌同类的牌出现了奇数次。
至于这两张牌之间的所有牌，由于它们都出现在栈顶出现，所以直接将其分别放在对应栈上即可。（当然一些牌会出现多次，在这种情况下为了方便，可以每次都将其放在同样的位置。）

于是策略便逐渐明朗起来：

策略 Meow：存在一个编号为 $sp$ 的空栈，且不满足策略1条件。

首先记录此时每类牌所在的栈编号和是否位于栈顶，记 $p_i$ 此时牌 $i$ 同类的牌所位于的栈编号， $t_i=1$ 代表此时牌 $i$ 同类的牌位于栈顶。

然后从牌堆顶的下一张开始，逐个向后判断。设当前判断的牌为 $x$ 。
- 若 $t_x=1$ ，则将 $x$ 放到栈 $p_x$ 的栈顶，然后判断下一张。
- 否则若 $x$ 与牌堆顶的牌同类，将这两张牌放到 $sp$ 里，然后更换使用策略1或重新使用策略 Meow。
- 否则：
  
  若与栈 $p_x$ 的栈顶牌同类的牌在牌堆顶至 $x$ 这些牌之间出现了奇数次，则将此时牌堆顶的牌放置于栈 $sp$ ，将 $x$ 放置于栈 $p_x$ ，然后将 $sp$ 改为 $p_x$ 。
  
  若与栈 $p_x$ 的栈顶牌同类的牌在牌堆顶至 $x$ 这些牌之间出现了偶数次，则将此时牌堆顶的牌放置于栈 $p_x$ ，将 $x$ 放置于栈 $sp$ ，然后在栈 $sp$ 和 $p_x$ 上执行一次操作 $2$ 。
  
  执行以上两种操作之一后更换使用策略1或重新使用策略 Meow 即可。
当然，由于将牌加入至栈的过程是有序的，所以在实现上会有些许不同。（例如，可以先找到 $x$ 在哪里，然后根据信息判断牌堆顶的牌应放置在哪里，最后将牌堆顶之后的牌加入栈。）

重复执行策略1和策略 Meow，最终所有的牌均可以被消掉。这样我们也可以证明所有合法的初始配置均有解。

整体操作示例

对于操作次数：我们会执行恰好 $m$ 次操作1，而每次操作2会消除两张牌，由于操作1执行过程中也会消去牌，因此 $2m$ 张牌至多使用 $m$ 次操作2即可全部消除，于是总操作次数不超过 $m+m=2m$ ，符合条件。

数据范围较大（ $\sum m\le 2\times 10^6$ ），所以需要注意复杂度和常数。

代码实现的细节和注意事项

维护信息

你需要维护：
- 大小不超过1的栈有哪些
- 每种牌在场上出现的次数
- 每种牌所在的栈的编号
当然你也可以维护更多的信息，例如每种牌是否位于栈顶或栈底等。

操作函数

由于需要涉及到很多情况，所以建议将操作写进一个函数以减少代码量。

以下为一种写法：
```
void change(int x,int y){
	ans.push_back({x,y});
	if(y==0){//y=0代表为操作1
		...//操作1
	}
	else{
		...//操作2
	}
}
...
change(4,0);//将牌堆顶的牌加入栈4
change(1,2);//对栈1和栈2执行操作2
```
你也可以在这个函数里进行对维护信息的修改。
```
#include<bits/stdc++.h>
using namespace std;
ifstream fin("meow.in");
ofstream fout("meow.out");
#define cin fin
#define cout fout
int a[2000005],p[1000],b[1005];
deque<int>q[1000];
vector<pair<int,int>>ans;
int pos=1,sz;
int cnt[1005];
queue<int>pq0;
void change(int x,int y){
	ans.push_back({x,y});
	if(y==0){
		pq0.push(x);
		if(!q[x].empty() and q[x].back()==a[pos]){
			q[x].pop_back();
			cnt[a[pos]]--;
			if(cnt[a[pos]]==0)sz--,p[a[pos]]=0;
			if(q[x].empty())b[a[pos]]=0;
		}
		else{
			q[x].push_back(a[pos]);
			if(cnt[a[pos]]==0){
				sz++,p[a[pos]]=x;
			}
			cnt[a[pos]]++;
			if(q[x].size()==1)b[a[pos]]=1;
		}
		pos++;
	}
	else{
		pq0.push(x);
		pq0.push(y);
		if(q[x].front()==q[y].front()){
			b[q[x].front()]=0;
			cnt[q[x].front()]-=2;
			if(cnt[q[x].front()]==0){
				sz--,p[q[x].front()]=0;
				b[q[x].front()]=0;
			}
			q[x].pop_front();
			q[y].pop_front();
			
			if(!q[x].empty())b[q[x].front()]=1;
			if(!q[y].empty())b[q[y].front()]=1;
		}
	}
}
int main(){
	int t;
	cin>>t;
	while(t--){
		pos=1;
		sz=0;
		memset(p,0,sizeof p);
		memset(b,0,sizeof b);
		ans.resize(0);
		int n,m,k;
		cin>>n>>m>>k;
		int sp=n;
		
		while(!pq0.empty())pq0.pop();
		for(int i=1;i<=n;i++){
			if(i!=sp)pq0.push(i);
		}
		int ap[k+5]={0};
		for(int i=1;i<=m;i++){
			cin>>a[i];
			a[i+1]=0;
		}
		for(int i=1;i<=m;i++){
			if(sz==2*(n-1) and !cnt[a[i]]){
				int ti=i;
				for(int j=i+1;j<=m;j++){
					if(a[j]==a[i]){
						for(int w=i+1;w<=j;w++){
							ap[a[w]]=p[a[w]];
						}
						change(sp,0);
							for(int w=i+1;w<=j;w++){
								if(a[w]==a[i])change(sp,0);
								else change(ap[a[w]],0);
							}
							
						i=j;
						break;
					}
					if(b[a[j]]){
						if(ap[q[p[a[j]]].back()]){
							for(int w=i+1;w<=j;w++){
								ap[a[w]]=p[a[w]];
							}
							change(sp,0);
							sp=p[a[j]];
							for(int w=i+1;w<=j;w++){
								change(ap[a[w]],0);
							}
							
							
						}
						else{
							for(int w=i+1;w<=j;w++){
								ap[a[w]]=p[a[w]];
							}
							change(p[a[j]],0);
							for(int w=i+1;w<j;w++){
								change(ap[a[w]],0);
							}
							change(sp,0);
							change(sp,p[a[j]]);
						}
						i=j;
						break;
					}
					else{
						ap[a[j]]^=1;
					}
				}
				for(int j=ti;j<=i;j++){
					ap[a[j]]=0;
				}
				continue;
			}
			if(p[a[i]]){
				if(q[p[a[i]]].back()==a[i]){
					change(p[a[i]],0);
				}
				else{
					change(sp,0);
					change(sp,p[a[i]]);
				}
			}
			else{
				while(!pq0.empty() and (pq0.front()==sp or q[pq0.front()].size()>=2)){
					pq0.pop();
				}
				change(pq0.front(),0);
			}
		}
		
		cout<<ans.size()<<endl;
		
		for(auto it:ans){
			if(it.second==0)cout<<1<<' '<<it.first<<'\n';
			else cout<<2<<' '<<it.first<<" "<<it.second<<'\n';
		}
		assert(pos==m+1);
		for(int i=1;i<=n;i++){
			assert(q[i].empty());
		}
	}
}
```